一、数组
1.1)什么是数组
数组是指有序的元素序列。如果将有限个类型相同的变量的集合命名,那么这个名称就是数组名,而组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。
1.2)数组的创建
数组的创建方式
type_t arr_name [const_n];
//type_t 是指数组的元素类型
//const_n 是一个常量表达式,用来指定数组的大小
数组创建的实例
//代码1
int arr1[10];
//代码2
int count = 10;
int arr2[count];//数组时候可以正常创建?
//代码3
char arr3[10];
float arr4[1];
double arr5[20];
注:数组创建,在C99标准之前, [ ] 中要给一个常量才可以,不能使用变量。在C99标准支持了变长数组的概念。
1.3)数组的初始化
数组的初始化是指,在创建数组的同时给数组的内容一些合理初始值(初始化)
int arr1[10] = {1,2,3};
int arr2[] = {1,2,3,4};
int arr3[5] = {1,2,3,4,5};
char arr4[3] = {'a',98, 'c'};
char arr5[] = {'a','b','c'};
char arr6[] = "abcdef";
数组在创建的时候如果想不指定数组的确定的大小就得初始化。数组的元素个数根据初始化的内容来确定
1.4)一维数组的使用
对于数组的使用我们之前介绍了一个操作符: [ ] ,下标引用操作符。它其实就数组访问的操作符
#include <stdio.h>
int main()
{
int arr[10] = {0};//数组的不完全初始化
//计算数组的元素个数
int sz = sizeof(arr)/sizeof(arr[0]);
//对数组内容赋值,数组是使用下标来访问的,下标从0开始。所以:
int i = 0;//做下标
for(i=0; i<10; i++)
{
arr[i] = i;
}
//输出数组的内容
for(i=0; i<10; ++i)
{
printf("%d ", arr[i]);
}
return 0;
}
总结:
- 数组是使用下标来访问的,下标是从0开始。
- 数组的大小可以通过计算得到。
1.5)一维数组在内存中的存储
#include <stdio.h>
int main()
{
int arr[10] = {0};
int i = 0;
int sz = sizeof(arr)/sizeof(arr[0]);
for(i=0; i<sz; ++i)
{
printf("&arr[%d] = %p\n", i, &arr[i]);
}
return 0;
}
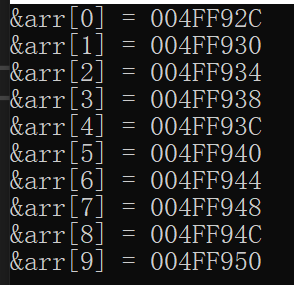
仔细观察输出的结果,我们知道,随着数组下标的增长,元素的地址,也在有规律的递增。
由此可以得出结论:数组在内存中是连续存放的。
1.6)二维数组的创建和初始化
1)二维数组的创建
//数组创建
int arr[3][4];
char arr[3][5];
double arr[2][4];
2) 二维数组的初始化
int arr[3][4] = {1,2,3,4};
int arr[3][4] = {{1,2},{4,5}};
int arr[][4] = {{2,3},{4,5}};//二维数组如果有初始化,行可以省略,列不能省略
3) 二维数组的使用
#include <stdio.h>
int main()
{
int arr[3][4] = { 0 };
int i = 0;
for (i = 0; i < 3; i++)
{
int j = 0;
for (j = 0; j < 4; j++)
{
arr[i][j] = i * 4 + j;
}
for (i = 0; i < 3; i++)
{
int j = 0;
for (j = 0; j < 4; j++)
{
printf("%d ", arr[i][j]);
}
}
return 0;
}
}
结果为 0 1 2 3 0 0 0 0 0 0
4)二维数组在内存中的存储
#include <stdio.h>
int main()
{
int arr[3][4];
int i = 0;
for (i = 0; i < 3; i++)
{
int j = 0;
for (j = 0; j < 4; j++)
{
printf("&arr[%d][%d] = %p\n", i, j, &arr[i][j]);
}
}
return 0;
}
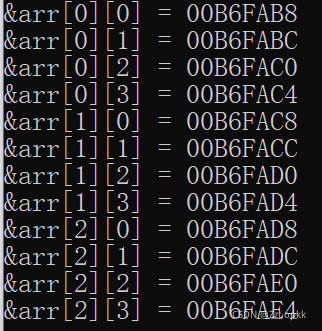
通过结果我们可以分析到,其实二维数组在内存中也是连续存储的
1.7)数组越界
数组的下标是有范围限制的。
数组的下规定是从0开始的,如果数组有n个元素,最后一个元素的下标就是n-1。
所以数组的下标如果小于0,或者大于n-1,就是数组越界访问了,超出了数组合法空间的访问。
C语言本身是不做数组下标的越界检查,编译器也不一定报错,但是编译器不报错,并不意味着程序就是正确的,
#include <stdio.h>
int main()
{
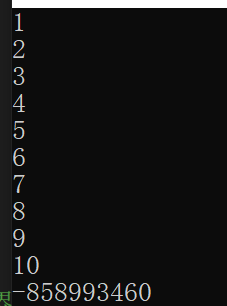
int arr[10] = {1,2,3,4,5,6,7,8,9,10};
int i = 0;
for(i=0; i<=10; i++)
{
printf("%d\n", arr[i]);//当i等于10的时候,越界访问了
}
return 0; }
1.8)数组小游戏
二、操作符
下面是我们要介绍的操作符
- 算术操作符
- 移位操作符
- 位操作符
- 赋值操作符
- 单目操作符
- 关系操作符
- 逻辑操作符
- 条件操作符
- 逗号表达式
- 下标引用、函数调用和结构成员
2.1)算术操作符
+ - * /
- 除了 % 操作符之外,其他的几个操作符可以作用于整数和浮点数。
- 对于 / 操作符如果两个操作数都为整数,执行整数除法。而只要有浮点数执行的就是浮点数除法。
- % 操作符的两个操作数必须为整数。返回的是整除之后的余数。
2.2)移位操作符
<< 左移操作符
>> 右移操作符
注:移位操作符的操作数只能是整数
2.2.1) 左移操作符
移位规则:
左边抛弃、右边补0
注:只要num没有被赋值,自身的值不会改变
2.2.1)右移操作符
移位规则:
首先右移运算分两种:
- 逻辑移位
左边用0填充,右边丢弃 - 算术移位
左边用原该值的符号位填充,右边丢弃
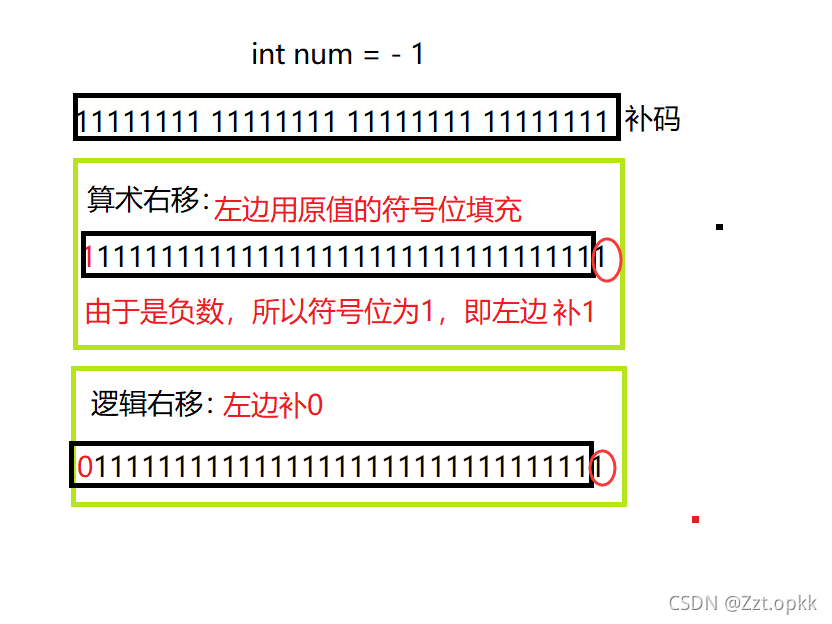
注:对于移位运算符,不要移动负数位,这个是标准未定义的。
例:
int num = 10;
num>>-1;//error
2.3)位操作符
位操作符有:
& 按位与
| 按位或
^ 按位异或
~ 取反
注:他们的操作数必须是整数
规则:
-
按位或运算
按位或运算符“|”是双目运算符。 其功能是参与运算的两数各对应的二进位相或。只要对应的二个二进位有一个为1时,结果位就为1。参与运算的两个数均以补码出现。 -
按位异或运算
按位异或运算符“^”是双目运算符。 其功能是参与运算的两数各对应的二进位相异或,当两对应的二进位相异时,结果为1。参与运算数仍以补码出现。 -
求反运算
求反运算符~为单目运算符,具有右结合性。 其功能是对参与运算的数的各二进位按位求反。 -
按位与运算
按位与运算符"&"是双目运算符。 其功能是参与运算的两数各对应的二进位相与。只有对应的两个二进位均为1时,结果位才为1 ,否则为0。参与运算的数以补码方式出现。
2.4)赋值操作符
=
复合赋值符
+=
-=
*=
/=
%=
>>=
<<=
&=
|=
^=
2.4)单目操作符
! 逻辑反操作
- 负值
+ 正值
& 取地址
sizeof 操作数的类型长度(以字节为单位)
~ 对一个数的二进制按位取反
-- 前置、后置--
++ 前置、后置++
* 间接访问操作符(解引用操作符) (类型) 强制类型转换
2.5)关系操作符
>
>=
<
<=
!= 用于测试“不相等”
== 用于测试“相等
2.6)逻辑操作符
&& 逻辑与
|| 逻辑或
&& 逻辑与,可以理解为并且的意思.只有当全部表达式为真时值为1,否则为0;
如果有多个表达式,应该从左到右依次看表达式真值,只要有一个表达式为假,就不需要扫描结果直接为0
|| 逻辑或,可以理解为或者的意思,也就是条件可以2取一,同理可知,只要从左到右表达式中找到了一个为真,就停止返回值为1,否则为0.
2.7)条件操作符
exp1 ? exp2 : exp3
解释:如果表达式1成立,则执行表达式2,否则执行表达式3
2.8)逗号表达式
逗号表达式,就是用逗号隔开的多个表达式。
逗号表达式,从左向右依次执行。整个表达式的结果是最后一个表达式的结果。
2.9) 下标引用、函数调用和结构成员
1)[ ] 下标引用操作符
操作数:一个数组名 + 一个索引值
int arr[10];//创建数组
arr[9] = 10;//实用下标引用操作符。
[ ]的两个操作数是arr和9
2) ( ) 函数调用操作符
接受一个或者多个操作数:第一个操作数是函数名,剩余的操作数就是传递给函数的参数。
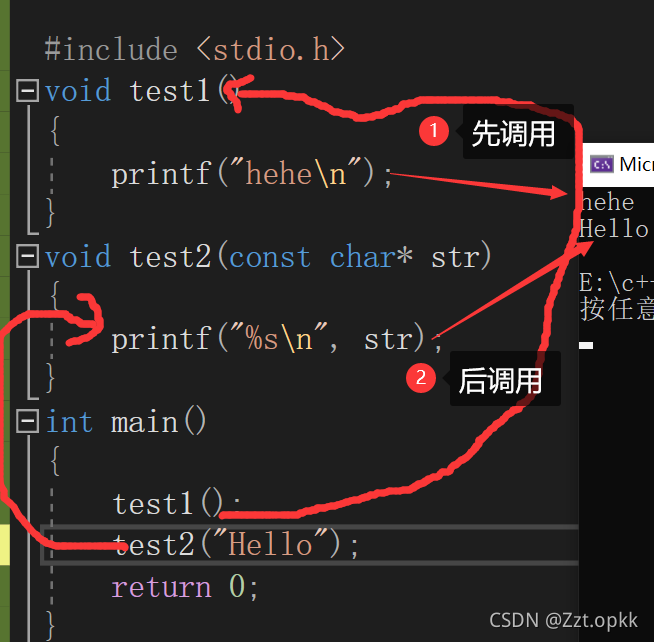
#include <stdio.h>
void test1()
{
printf("hehe\n");
}
void test2(const char* str)
{
printf("%s\n", str);
}
int main()
{
test1();
test2("Hello");
return 0;
}
3)访问一个结构的成员
. 结构体.成员名
-> 结构体指针->成员名
#include <stdio.h>
struct Stu
{
char name[10];
int age;
char sex[5];
double score;
};
void set_age1(struct Stu stu)
{
stu.age = 18;
}
void set_age2(struct Stu* pStu)
{
pStu->age = 18;//结构成员访问
}
int main()
{
struct Stu stu;
struct Stu* pStu = &stu;//结构成员访问
stu.age = 20;//结构成员访问
set_age1(stu);
pStu->age = 20;//结构成员访问
set_age2(pStu);
return 0;
}
2.10)表达式求值
表达式求值的顺序一部分是由操作符的优先级和结合性决定。
同样,有些表达式的操作数在求值的过程中可能需要转换为其他类型
1)隐式类型转换
C的整型算术运算总是至少以缺省整型类型的精度来进行的。
为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
整型提升的意义:
- 表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
- 因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
- 通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行运算。
如何进行整体提升呢?
整形提升是按照变量的数据类型的符号位来提升的
//负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位:
1111111
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为1
提升之后的结果是:
11111111111111111111111111111111
//正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位:
00000001
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为0
提升之后的结果是:
00000000000000000000000000000001
//无符号整形提升,高位补0
2) 算术转换
如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数的转换为另一个操作数的类型,否则操作就无法进行。下面的层次体系称为寻常算术转换。
long double
double
float
unsigned long int
long int
unsigned int
int
如果某个操作数的类型在上面这个列表中排名较低,那么首先要转换为另外一个操作数的类型后执行运算。
注:
float f = 3.14;
int num = f;//隐式转换,会有精度丢失
3) 操作符的属性
复杂表达式的求值有三个影响的因素。
- 操作符的优先级
- 操作符的结合性
- 是否控制求值顺序。
两个相邻的操作符先执行哪个?取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。
| 操作符 | 描述 | 用法示例 | 结果类型 | 结合性 | 是否控制求值顺序 |
|---|---|---|---|---|---|
| () | 聚组 | (表达式) | 与表达式同 | N/A | 否 |
| () | 函数调用 | rexp(rexp,…,rexp) | rexp | L-R | 否 |
| [ ] | 下标引用 | rexp[rexp] | lexp | L-R | 否 |
| . | 访问结构成员 | lexp.member_name | lexp | L-R | 否 |
| -> | 访问结构指针成员 | rexp->member_name | lexp | L-R | 否 |
| ++ | 后缀自增 | lexp ++ | rexp | L-R | 否 |
| - - | 后缀自减 | lexp - - | rexp | L-R | 否 |
| ! | 逻辑反 | ! rexp | rexp | R-L | 否 |
| ~ | 按位取反 | ~ rexp | rexp | R-L | 否 |
| + | 单目,表示正值 | + rexp | rexp | R-L | 否 |
| - | 单目,表示负值 | - rexp | rexp | R-L | 否 |
| ++ | 前缀自增 | ++ lexp | rexp | R-L | 否 |
| – | 前缀自减 | – lexp | rexp | R-L | 否 |
| * | 间接访问 | * rexp | lexp | R-L | 否 |
| & | 取地址 | & lexp | rexp | R-L | 否 |
| sizeof | 取其长度,以字节表示 | sizeof rexp sizeof(类 型) | rexp | R-L | 否 |
| (类型) | 类型转换 (类型) | rexp | rexp | R-L | 否 |
| * | 乘法 | rexp * rexp | rexp | L-R | 否 |
| / | 除法 | rexp / rexp | rexp | L-R | 否 |
| % | 整数取余 | rexp % rexp | rexp | L-R | 否 |
| + | 加法 | rexp + rexp | rexp | L-R | 否 |
| - | 减法 | rexp - rexp | rexp | L-R | 否 |
| << | 左移位 | rexp << rexp | rexp | L-R | 否 |
| >> | 右移位 | rexp >> rexp | rexp | L-R | 否 |
| >> | 大于 | rexp > rexp | rexp | L-R | 否 |
| >= | 大于等于 | rexp >= rexp | rexp | L-R | 否 |
| < | 小于 | rexp < rexp | rexp | L-R | 否 |
| <= | 小于等于 | rexp <= rexp | rexp | L-R | 否 |
| == | 等于 | rexp == rexp | rexp | L-R | 否 |
| != | 不等于 | rexp != rexp | rexp | L-R | 否 |
| & | 位与 | rexp & rexp | rexp | L-R | 否 |
| ^ | 位异或 | rexp ^ rexp | rexp | L-R | 否 |
| 1 | 位或 | rexp 1 rexp | rexp | L-R | 否 |
| && | 逻辑与 | rexp && rexp | rexp | L-R | 是 |
| 11 | 逻辑或 | rexp 11 rexp | rexp | L-R | 是 |
| ? : | 条件操作符 | rexp ? rexp : rexp | rexp | N/A | 是 |
| = | 赋值 | lexp = rexp | rexp | R-L | 否 |
| += | 以…加 | lexp += rexp | rexp | R-L | 否 |
| -= | 以…减 | lexp -= rexp | rexp | R-L | 否 |
| *= | 以…乘 | lexp *= rexp | rexp | R-L | 否 |
| /= | 以…除 | lexp /= rexp | rexp | R-L | 否 |
| %= | 以…取模 | lexp %= rexp | rexp | R-L | 否 |
| <<= | 以…左移 | lexp <<= rexp | rexp | R-L | 否 |
| >>= | 以…右移 | lexp >>= rexp | rexp | R-L | 否 |
| &= | 以…与 | lexp &= rexp | rexp | R-L | 否 |
| ^= | 以…异或 | lexp ^= rexp | rexp | R-L | 否 |
| 1= | 以…或 | lexp 1= rexp | rexp | R-L | 否 |
| , | 逗号 | rexp,rexp | rexp | L-R | 是 |
