01背包/图的m着色/n后问题【回溯】(C语言)
有n 个物品,它们有各自的重量和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和。
代码
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
int max = 0;
int maxx[MAXSIZE];
int x[MAXSIZE];
int w[MAXSIZE] = {0,2,20,5,10,5};
int v[MAXSIZE] = {0,8,50,12,21,10};
int bagweight = 30;
int thingnum = 5;
void output()
{
int i;
printf("最大的价值是:%d\n",max);
for(i=1;i<=thingnum;i++)
{
printf("%-5d",maxx[i]);
}
}
int jianzhi(int t)
{
int i;
int sum = 0;
for(i=t+1;i<=thingnum;i++)
{
sum = sum + v[i];
}
return sum;
}
void bactrack(int t,int cw,int cv)
{
int i;
if(t>thingnum)
{
if(cv>=max)
{
for(i=1;i<=thingnum;i++)
{
maxx[i] = x[i];
}
max = cv;
}
}
else
{
x[t]=1;
if(cw+w[t]<=bagweight) bactrack(t+1,cw+w[t],cv+v[t]);
x[t]=0;
if(cv+jianzhi(t)>max)
{
bactrack(t+1,cw,cv);
}
}
}
int main()
{
int i,j;
for(i=0;i<=thingnum;i++)
{
x[i] = 0;
maxx[i]=0;
}
bactrack(1,0,0);
output();
}

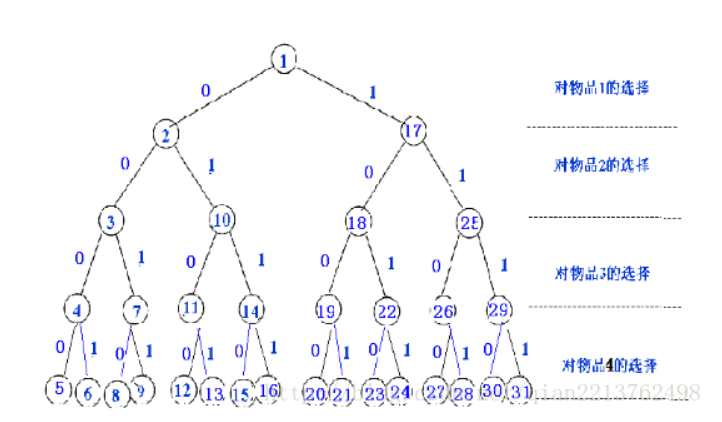
图的m着色问题
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
四色猜想:四色问题是m图着色问题的一个特例,根据四色原理,证明平面或球面上的任何地图的所有区域都至多可用四种、颜色来着色,并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可转换成对一平面图的4-着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。将地图的每个区域变成一个结点,若两个区域相邻,则相应的结点用一条边连接起来。

代码
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 5
int max = 0;
int maxx[MAXSIZE];
int x[MAXSIZE];
int thingnum = 5; //节点数
int colornum = 4;//上色数量
int a[MAXSIZE][MAXSIZE];
long sum = 0;//当前已找到的可m着色的方案数目
int OK(int t)
{
int i;
for(i=1;i<=thingnum;i++)
{
if((a[t][i]==1) && (x[i]==x[t])) return 0;
}
return 1;
}
void bactrack(int t)
{
int i;
if(t>thingnum)
{
sum++;
for(i=1;i<=thingnum;i++)
{
printf("%5d",x[i]);
}
printf("\n");
}
else
{
for(int i=1;i<=colornum;i++)
{
x[t] = i;
if(OK(t)) bactrack(t+1);
x[t] = 0;
}
}
}
int main()
{
int i,j;
for(i=0;i<=thingnum;i++)
{
for(j=0;j<=thingnum;j++)
{
scanf("%d",&a[i][j]);
}
x[i] = 0;
}
bactrack(1);
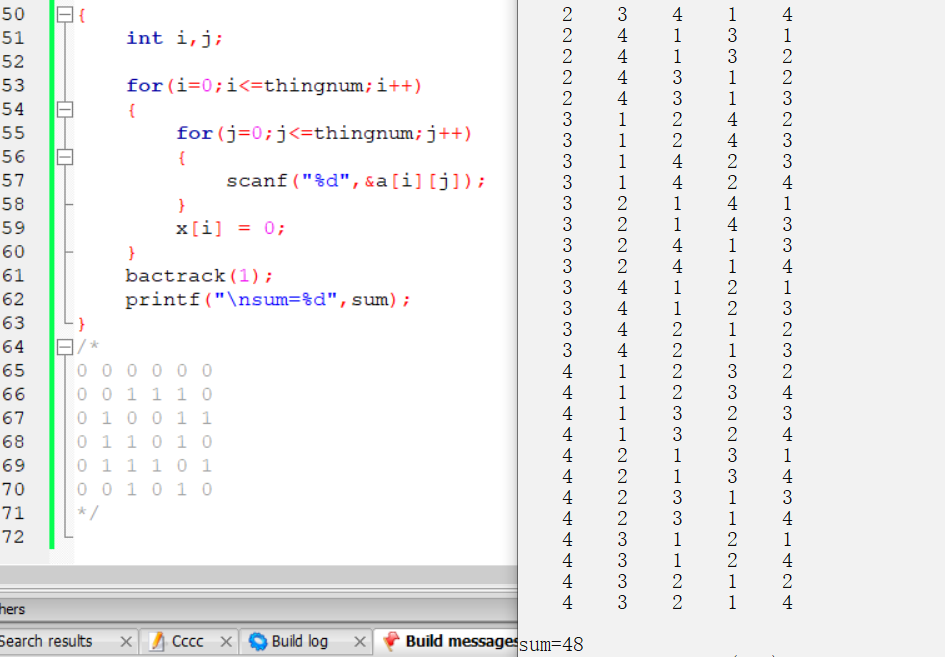
printf("\nsum=%d",sum);
}
/*
0 0 0 0 0 0
0 0 1 1 1 0
0 1 0 0 1 1
0 1 1 0 1 0
0 1 1 1 0 1
0 0 1 0 1 0
*/
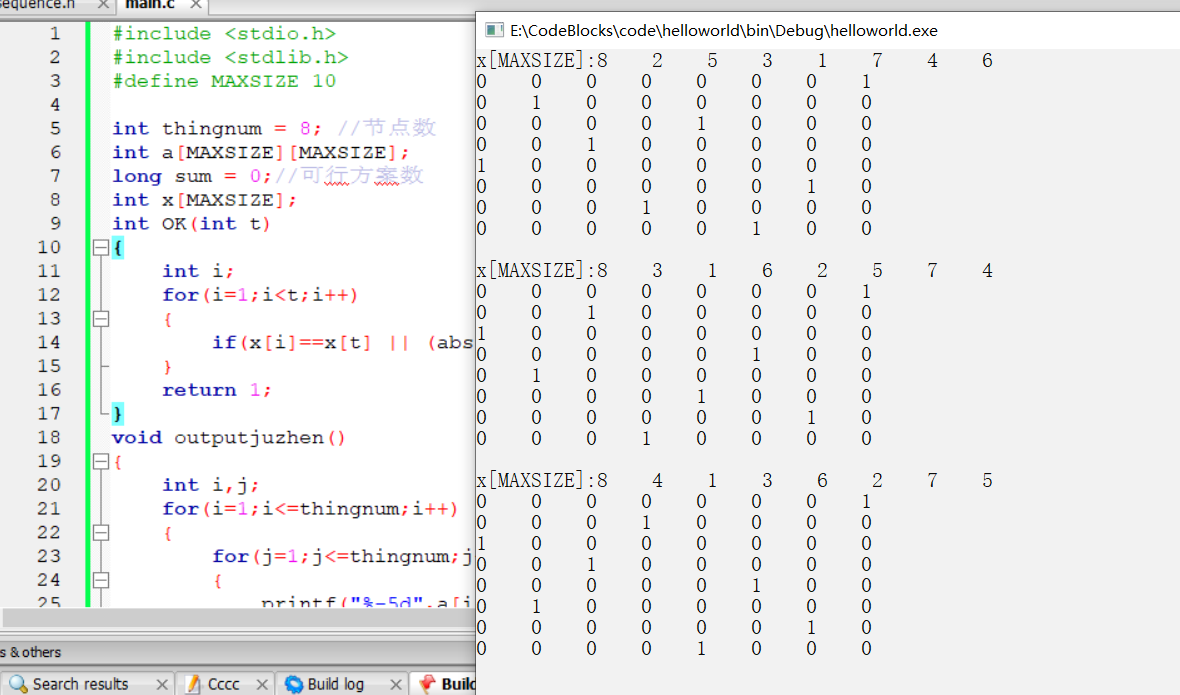
n皇后问题
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。

代码
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
int thingnum = 8; //节点数
int a[MAXSIZE][MAXSIZE];
long sum = 0;//可行方案数
int x[MAXSIZE];
int OK(int t)
{
int i;
for(i=1;i<t;i++)
{
if(x[i]==x[t] || (abs(t-i)==abs(x[t]-x[i]))) return 0;
}
return 1;
}
void outputjuzhen()
{
int i,j;
for(i=1;i<=thingnum;i++)
{
for(j=1;j<=thingnum;j++)
{
printf("%-5d",a[i][j]);
}
printf("\n");
}
for(i=1;i<=thingnum;i++)
{
for(j=1;j<=thingnum;j++)
{
a[i][j]=0;
}
}
}
void bactrack(int t)
{
int i;
if(t>thingnum)
{
sum++;
printf("x[MAXSIZE]:");
for(i=1;i<=thingnum;i++)
{
printf("%-5d",x[i]);
a[i][x[i]] = 1;
}
printf("\n");
outputjuzhen();
printf("\n");
}
else
{
for(int i=1;i<=thingnum;i++)
{
x[t] = i;
if(OK(t)) bactrack(t+1);
}
}
}
int main()
{
int i,j;
for(i=0;i<=thingnum;i++)
{
for(j=0;j<=thingnum;j++)
{
a[i][j]=0;
}
x[i]=0;
}
bactrack(1);
printf("\nsum=%d",sum);
}