栈和队列
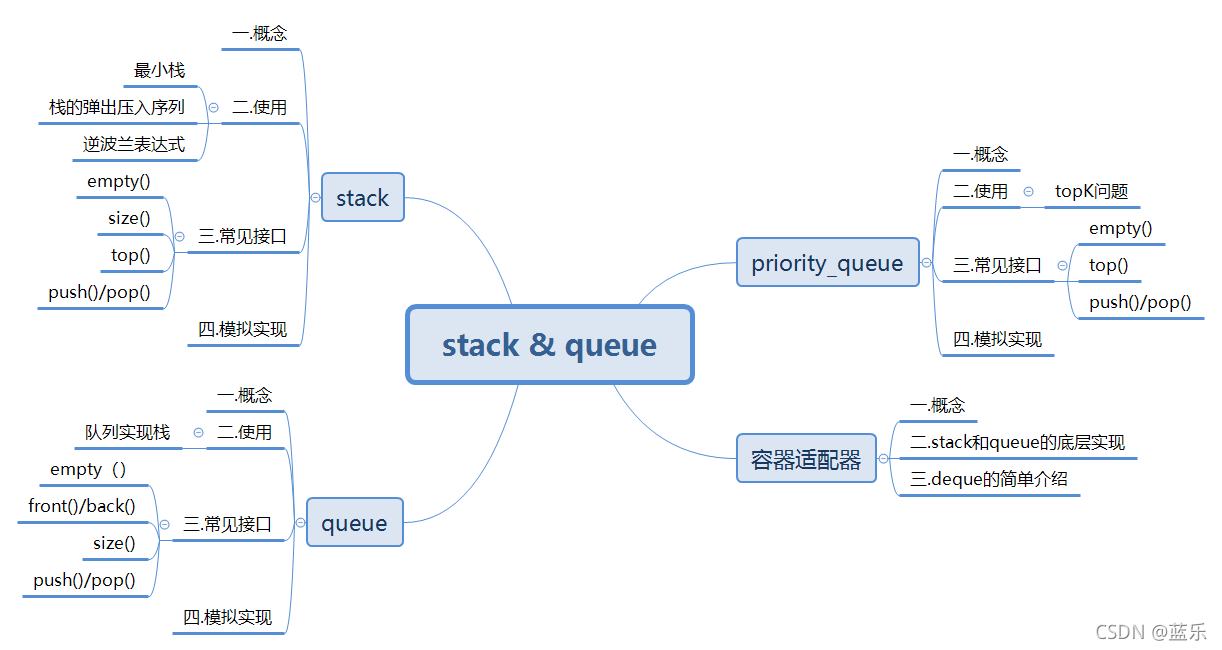
一.stack的介绍和使用
(1)概念
·stack是一种后进先出的容器结构,准确来说stack并不是容器,而是一种容器适配器(对特定类封装作为其底层的容器)。
(2)常见接口
| 函数说明 | 接口说明 |
|---|---|
| stack() | 构造空的栈 |
| empty() | 判断栈是否为空 |
| size() | 返回stack中的元素个数 |
| top() | 返回栈顶元素的引用 |
| push() | 将元素压入stack中 |
| pop() | 将stack栈顶的元素弹出 |
(3)使用
1.最小栈问题
最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
思路:使用两个栈,一个正常存放元素,另一个存放最小值,每次入栈时比较更新即可。
class MinStack {
public:
MinStack() {
}
void push(int val) {
if(_minst.empty() || val <= _minst.top())//_minst为空或者val值小于_minst中最小值则入栈
{
_minst.push(val);
}
_st.push(val);
}
void pop() {
if(_minst.top() == _st.top())//若_st出栈的刚好为最小值,则_minst亦出栈
{
_minst.pop();
}
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};
2.栈的压入、弹出序列
栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。
思路:用一个栈模拟栈的压入、弹出即可,每次将压入顺序数组的元素入栈,然后若栈顶元素与弹出顺序的数组元素相同,那么直到栈顶与之不同之前,都将栈中元素出栈。
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> st;
int pushi = 0, popi = 0;
while(pushi < pushV.size())//当pushi未到尽头时就将pushi入栈
{
st.push(pushV[pushi++]);
while(!st.empty() && st.top() == popV[popi])//若st栈顶元素与popi处相同则出栈
{
popi++;
st.pop();
}
}
//若此时st为空,则入出栈对应
return st.empty();
}
};
3.逆波兰表达式
逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。*
详细参见文章:
逆波兰表达式
(4)stack 的模拟实现
//Container时容器适配器,默认是deque,即双端队列
template <class T, class Container = deque<T>>
class stack
{
private:
Container _c;
};
二.queue的介绍和使用
(1)概念
·队列是一种后进后出的容器适配器结构,标准容器类deque和list满足其要求。默认情况下,如果没有为queue实例化指定容器类,则使用标准容器deque(双端队列)。
(2)常见接口
| 函数说明 | 接口说明 |
|---|---|
| queue() | 构造空的队列 |
| empty() | 判断队列是否为空 |
| size() | 返回队列中元素的个数 |
| front() | 返回队头元素 |
| back() | 返回对尾元素 |
| pop() | 将队头元素出队 |
(3)使用
用队列使用栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
用队列实现栈
思路:保证有一个栈始终为空,另一个接受元素。若元素入队,则入非空栈中;若出队头元素,则将一个栈中的元素倒到另一个栈,直到只剩一个元素再出栈即可:
class MyStack {
public:
MyStack() {
}
void push(int x) {
if(!_q1.empty())
{
_q1.push(x);
}
else
{
_q2.push(x);
}
}
int pop() {
if(!_q1.empty())
{
while(_q1.size() != 1)
{
_q2.push(_q1.front());
_q1.pop();
}
int top = _q1.front();
_q1.pop();
return top;
}
else
{
while(_q2.size() != 1)
{
_q1.push(_q2.front());
_q2.pop();
}
int top = _q2.front();
_q2.pop();
return top;
}
}
int top() {
if(!_q1.empty())
{
while(_q1.size() != 1)
{
_q2.push(_q1.front());
_q1.pop();
}
int top = _q1.front();
_q1.pop();
_q2.push(top);
return top;
}
else
{
while(_q2.size() != 1)
{
_q1.push(_q2.front());
_q2.pop();
}
int top = _q2.front();
_q2.pop();
_q1.push(top);
return top;
}
}
bool empty() {
return _q1.empty() && _q2.empty();
}
private:
queue<int> _q1;
queue<int> _q2;
};
(4)queue的模拟实现
与stack类似的:
template <class T, class Container = deque<T>>
class queue
{
private:
Container _c;
};
三、priority_queue的介绍和使用
(1)概念
·优先队列是一种容器适配器,根据严格的弱排序标准(默认情况),它的第一个元素总是它所包含的元素中最大的。
·简单来说,priority_queue类似于数据结构中的堆,其使用与实现也和堆(Heap)并无二异。
(2)常见接口
| 函数说明 | 接口说明 |
|---|---|
| priority_queue() | 构造一个空的优先级队列 |
| empty() | 判断优先级队列是否为空 |
| top() | 返回优先级队列中最大(最小)元素,即堆顶元素 |
| push() | 在优先级队列中插入元素 |
| pop() | 删除优先级队列中最大(最小)元素,即堆顶元素 |
(3)使用
TopK问题
数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
思路:使用一个k个数降序的优先级队列(小堆),先将数组中前k个元素入堆,然后遍历数组中剩下的元素,若其大于堆顶元素(堆中最大的元素),则将其入堆,这样最终堆顶元素就是数组中的第k和最大元素,整个堆就是数组中最大的k个数。
这样理解:若数组元素比堆顶元素(最大的元素)还要大,那么将其进堆,最终的小堆就是数组中最大的k个元素。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
if(nums.size() == 1)
{
return nums[0];
}
//建k个数的小堆
priority_queue<int, vector<int>, greater<int>> pq;
//将数组中的前k个数进堆
for(int i = 0; i < k; i++)
{
pq.push(nums[i]);
}
//将数组中剩下的数与堆顶元素比较,若大于堆顶,则弹出堆顶元素,并将数组的数入堆
for(int i = k; i < nums.size(); i++)
{
if(pq.top() < nums[i])
{
pq.pop();
pq.push(nums[i]);
}
}
//最后,堆顶元素即为第k个最大的元素
return pq.top();
}
};
(4)priority_queue的模拟实现
仿函数的简单介绍
由于优先级队列的默认顺序是升序,而我们如果要让priority_queue的顺序改为降序(大堆),对于C语言就是用一个函数指针,而对于C++则可以使用仿函数。
C++中,通过在一个类中重载括号运算符的方法使用一个函数对象而不是一个普通函数来实现仿函数。
比如:
//构造一个小堆,其中,greater就是仿函数作为参数
priority_queue<int,vector<int>,greater<int>> q(v.begin(), v.end());
代码实现
template <class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
private:
Container _con;
};
四、容器适配器
(1)容器适配器的概念
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。上面介绍的stack、queue(默认deque)以及priority_queue(默认vector)都是容器适配器。
(2)deque的简单介绍
在上面我们认识了deque这种结构,即双端队列,那么它是怎么实现的呢?我们来简单了解一下。
1.deque的概念
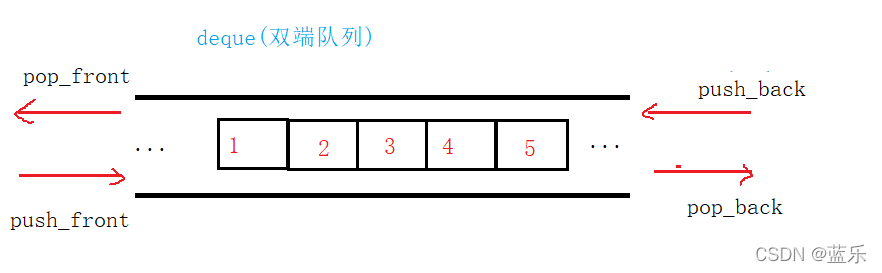
deque虽然叫做双端队列,但是它本质上不是一个队列。从逻辑结构上来看,deque是可以支持随机访问并且在任意位置插入删除的结构。这么一看可能会觉得deque的功能很强大,那么为什么实际上其使用却并不多呢?这就要来看deque的底层结构了。
2.deque底层结构的简单介绍
·deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。
·deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组。双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问的假象,落在了deque的迭代器身上,因此deque的迭代器设计就比较复杂,如下图所示:
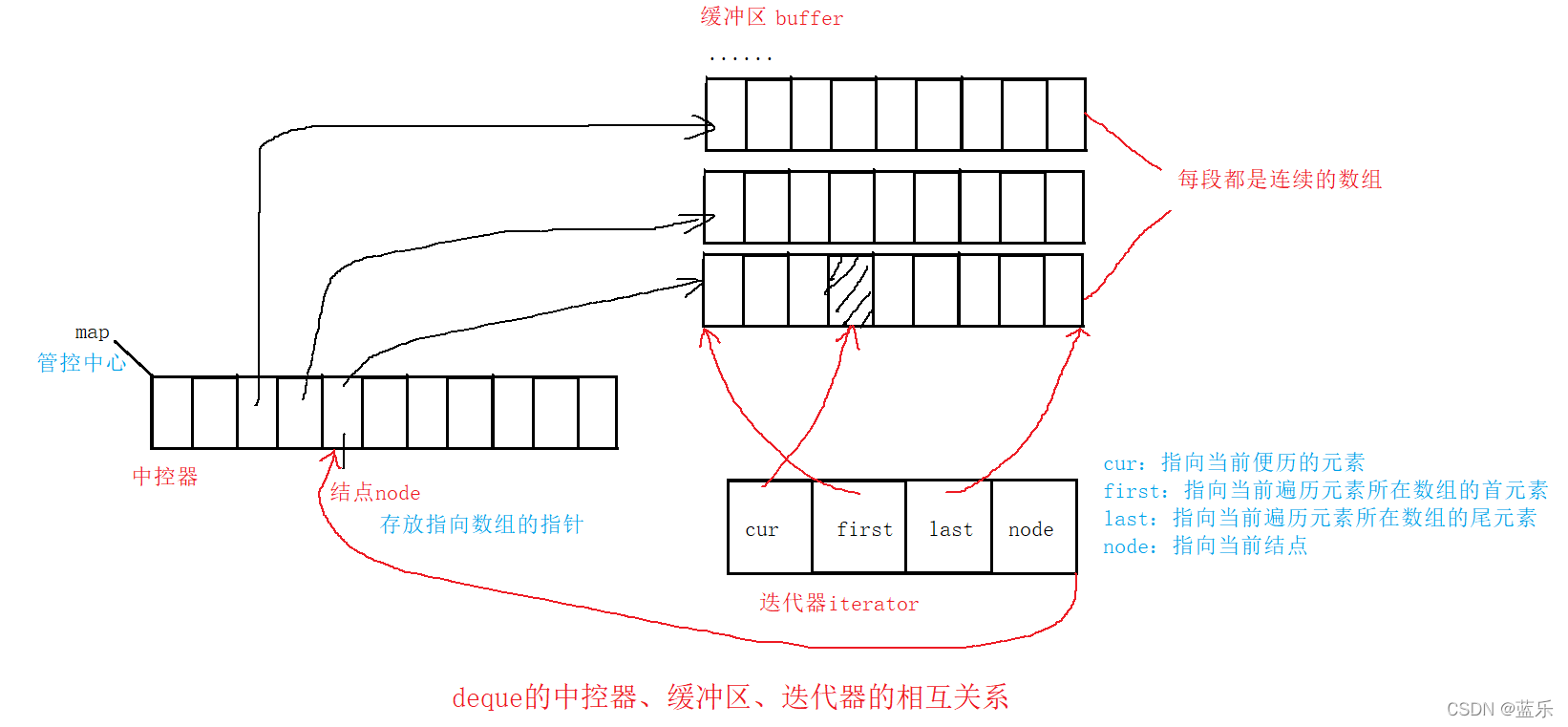
3.deque的优缺点
- 与vector比较,头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不需要搬移大量的元素,因此其效率是比vector高的。(时间复杂度O(1))
- 与list比较,首先deque可以随机访问;其次deque的底层是连续空间,空间利用率比较高,不需要存储额外字段。
- 但是deque也有致命缺陷:首先,不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下;而序列式场景中,可能需要经常遍历。其次,deque对于中间位置频繁的插入删除效率极低,甚至可能低于vector。因此在实际中,需要线性结构
时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构。
4.deque的应用
在上面我们所学到的stack和queue由于不会在中间频繁地插入删除,并且只需要对头和尾进行操作,其次,stack和queue都不需要遍历。因此,使用deque作为stack和queue的默认底层模板结构可以使栈和队列的操作保证和常数级的时间复杂度。