[C++知识库]【C语言】浮点数的存储形式

（一）引入浮点数

浮点数：就是计算机中的小数，按精度可分为单精度的float类型、双精度的double类型

我们通过一个简单的程序来重新认识下浮点数float类型（4字节）

#include <stdio.h>
int main()
{
	int a = 0x41440000;
	int* p = &a;
	float* fp = (float*)&a;
	
	printf("*p = %d\n", *p);
	printf("*fp = %f\n", *fp);
	return 0;
}

emmmm，这个程序的结果是什么呢？？思考一会，我们来看看结果吧

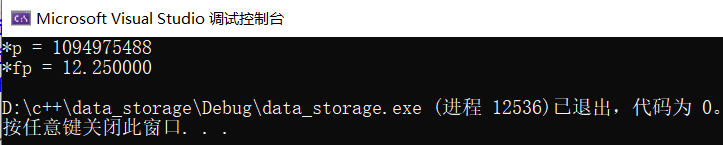
可以看到*p就是0x41440000转成整型输出1094975488，这个没什么问题，关键问题在于同样的地址，使用float类型的指针来对该地址解析就成了12.250000

可以这样说，浮点数的存储方式和整型数据存储形式完全不同呢！！

（二）浮点数的详细解读

（1）一个公式表示浮点数

国际标准IEEE(电气工程师学会)表示：任意一个浮点数的二进制形式X都可以用下面这个公式来表示。
X = (-1)^S * M * 2^E

• X: 表示一个浮点数的二进制形式
• (-1)^S: 确定符号位，当S == 0，表示该浮点数是正数；S == 1，表示该浮点数是负数
• M: 表示有效数字（M范围[ 1, 2 )，需要通过左/右移动小数点来使整数部分处于该范围内 ）
• 2^E: 表示指数位

由于有些浮点数比较复杂，所以暂时使用四字节的12.25来作为栗子

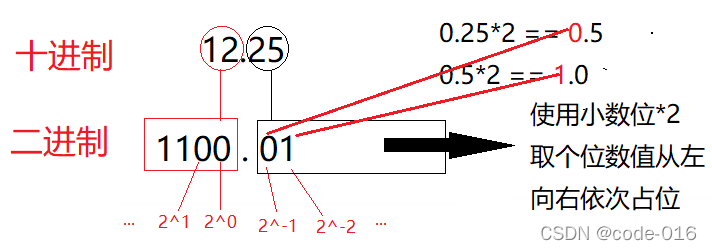
因为：12.25 > 0, 所以：(-1)^S 中的S== 0
因为：1100.01 ，要想使M满足[1, 2)，需要将小数点左移动3位，M == 1.10001，所以E == 3
此时的X == (-1)^0 * 1.10001 * 2^3 等价于1100.01

那再试试-0.25这个呢
S == 1
二进制：-0. 01 可右移2位，使M == 1满足条件，E == -2
X == (-1)^ 1 * 1 * 2^(-2);

所以我们现在把12.25用这个公式表示出来了，但是但是，我们需要知道是如何存储在内存中的啊喂

（2）内存中的浮点数

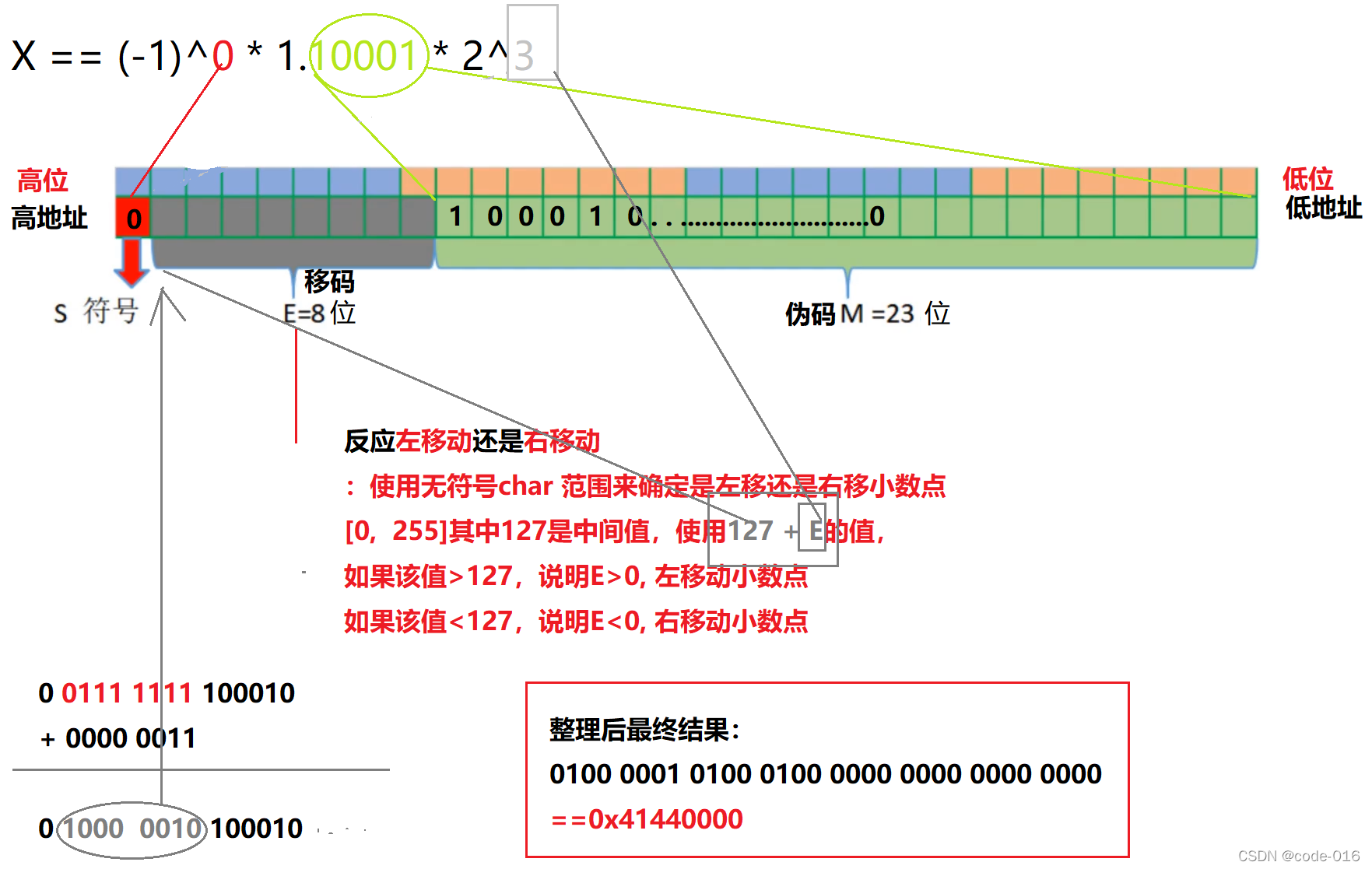
看到这里想必，你已经知道了（一）中的*fp的结果为什么是12.25了吧，并且通过内存中存储（小端）的值，也是和我们推出来是一致的。