[C++知识库]楚列斯基分解法、求矩阵范数的C++实现

这次的作业如下：

随机生成一个 $n$ 阶方阵与 $n$ 阶向量构成 $Ax=b$

• 构建 $n$ 阶对称正定矩阵
  1. 使用楚列斯基分解求 $x$
  2. 使用改进的楚列斯基分解求 $x$
• 构建 $n$ 阶对角占优不可约的三对角矩阵
  1. 使用简化计算的 $LU$ 分解求 $x$
• 求以上矩阵的条件数
  1. 包括 $1$-范数、$2$-范数和 $\infty$-范数的条件数

总结一下难点：

1. 快速生成 $n$ 阶对称正定矩阵
2. 矩阵求逆
3. 计算矩阵最大特征值

解决过程如下：

快速生成 $n$ 阶对称正定矩阵

如果随机生成对称矩阵，再判断是否正定，那么复杂度是很高的。我测试的时候，6阶矩阵已经跑不出来了。

百度找了一个方案：

1.随机生成一个单位正交阵A
2.随机生成一个对角元素均大于0的对角矩阵B
3.$C=AB{A}^T$即为一个正定矩阵

这样复杂度为 $O(n^3)$ 就可以接受了。

矩阵求逆

在计算矩阵条件数的时候，需要求给定矩阵的逆矩阵。方法如下：

首先，写出增广矩阵 A|E，即矩阵A右侧放置一个同阶的单位矩阵，得到一个新矩阵。
然后进行初等行变换，当把A转换为单位矩阵的时候，右边就是该矩阵的逆矩阵。

这个实现起来很简单，小改一下 Gauss 消元模板就行了。

计算矩阵最大特征值

在求矩阵的$2$-范数的时候，需要计算给定矩阵的最大特征值。

$$|\lambda E?A|=\left|\begin{array}{ccc}\lambda ?a_{11}& ?a_{12}& ?a_{13}\\ ?a_{21}& \lambda ?a_{22}& ?a_{23}\\ ?a_{31}& ?a_{32}& \lambda ?a_{33}\end{array}\right|=0$$

计算矩阵特征值需要解一个形如上面等式的方程。

这并不容易（但有办法）。在网上查找解决方案的时候，发现有人写了一个 Eigen 库，里面有很多关于矩阵的函数。于是按着教程下载了这个库，去官网查了查使用手册，实现了这个功能。参考链接

eigen3 就是下载好的第三方库，写好 main.cpp 后，在命令行编译：

g++ main.cpp -o main -I .\eigen3 -w

编译时可能会报无数的 warning ，使用 -w 参数忽略警告。然后就可以运行代码了。

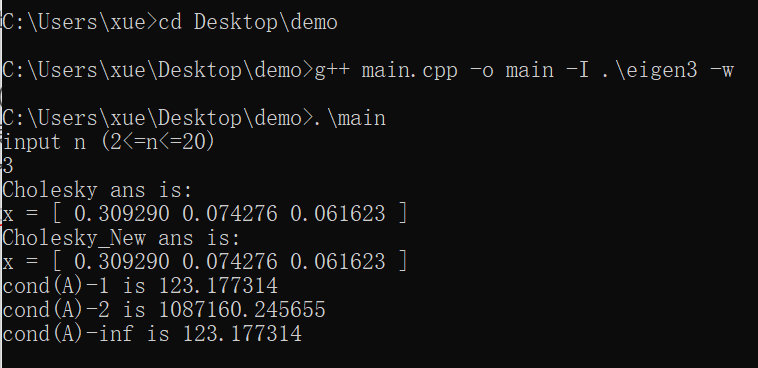
下面的代码是使用楚列斯基分解，及优化后的楚列斯基方法求 $x$。并且算出矩阵 $1$-范数、$2$-范数和 $\infty$-范数的条件数。

测试代码的时候，不要把 $n$ 输入太大，否则会有精度问题，或者上溢 double 。 $n$ 最好不超过20。

#include<bits/stdc++.h>
#include<Eigen/Dense>
#include<Eigen/Eigenvalues>
using namespace std;
using namespace Eigen;
const double eps=1e-6;
const int N=210;
int n,flag,bg,ed;
double acp[N][N],a[N][N],l[N][N],y[N],x[N],t[N][N],d[N],tmp[N][N];

void init(){ for(int i=1;i<=n;i++) for(int j=1;j<=n+1;j++) a[i][j]=acp[i][j]; }
void pt(auto a){ for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) printf("%lf%c",a[i][j]," \n"[j==n]); }
void out(){ printf("x = [ "); for(int i=1;i<=n;i++) printf("%lf ",x[i]); printf("]\n"); }

void mul(auto &a,auto &b){		//两矩阵相乘
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			tmp[i][j]=0;
			for(int k=1;k<=n;k++)
				tmp[i][j]+=a[i][k]*b[k][j];
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			a[i][j]=tmp[i][j];
}

void randinit(){	//随机生成对称正定矩阵
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(j>i) acp[i][j]=l[j][i]=0;
			else acp[i][j]=l[j][i]=(rand()%200)/10.0-10;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(i==j) a[i][j]=(rand()%10);
	mul(acp,a);
	mul(acp,l);
	for(int i=1;i<=n;i++) acp[i][n+1]=(rand()%200)/10.0-10;
}

void Cholesky(){
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++){
			l[i][j]=a[i][j];
			for(int k=1;k<=j-1;k++) l[i][j]-=l[i][k]*l[j][k];
			if(i==j) l[i][j]=sqrt(l[i][j]);
			else l[i][j]/=l[j][j];
			l[j][i]=l[i][j];
		}
}

void CholeskyAns(){
	for(int i=1;i<=n;i++){	//计算y[i]
		y[i]=a[i][n+1];
		for(int k=1;k<=i-1;k++) y[i]-=l[i][k]*y[k];
		y[i]/=l[i][i];
	} 
	for(int i=n;i>=1;i--){	//计算x[i]
		x[i]=y[i];
		for(int k=i+1;k<=n;k++) x[i]-=l[k][i]*x[k];
		x[i]/=l[i][i];
	}
}

void Cholesky_New(){
	d[1]=a[1][1];
	for(int i=2;i<=n;i++)
		for(int j=1;j<i;j++){
			t[i][j]=a[i][j];
			for(int k=1;k<=j-1;k++) t[i][j]-=t[i][k]*l[j][k];
			t[j][i]=t[i][j];
			l[i][j]=l[j][i]=t[i][j]/d[j];
			d[i]=a[i][i];
			for(int k=1;k<=i-1;k++) d[i]-=t[i][k]*l[i][k];
		}
}

void CholeskyAns_New(){
	for(int i=1;i<=n;i++){
		y[i]=a[i][n+1];
		for(int k=1;k<=i-1;k++) y[i]-=l[i][k]*y[k];
	}
	for(int i=n;i>=1;i--){
		x[i]=y[i]/d[i];
		for(int k=i+1;k<=n;k++) x[i]-=l[k][i]*x[k];
	}
}

double det(){	//计算det
	double ret=1;
	for(int i=1;i<=n;i++){
		int mx=i;
		for(int j=i+1;j<=n;j++) if(a[j][i]>a[mx][i]) mx=j;
		if(abs(a[mx][i])<eps){ flag=true; return 0; }
		if(mx!=i) ret=-ret;
		ret*=a[mx][i];
		for(int j=i;j<=n+1;j++) swap(a[i][j],a[mx][j]);
		for(int j=n+1;j>=i;j--) a[i][j]/=a[i][i];
		for(int k=1;k<=n;k++) if(i!=k)
			for(int j=n+1;j>=i;j--) a[k][j]-=a[k][i]*a[i][j];
	}
	return ret;
}

void getReverse(auto a){	//矩阵求逆
	for(int i=1;i<=n;i++) for(int j=n+1;j<=n+n;j++) a[i][j]=(i+n==j);
	for(int i=1;i<=n;i++){
		int mx=i;
		for(int j=i+1;j<=n;j++)
			if(a[j][i]>a[mx][i]) mx=j;
		if(abs(a[mx][i])<eps) return (void)(flag=true);
		for(int j=i;j<=n+n;j++) swap(a[i][j],a[mx][j]);
		for(int j=n+n;j>=i;j--) a[i][j]/=a[i][i];
		for(int k=1;k<=n;k++) if(i!=k)
			for(int j=n+n;j>=i;j--) a[k][j]-=a[k][i]*a[i][j];
	}
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]=a[i][j+n];
}

double calc(auto &a){		//计算矩阵最大特征值
	double mx=-1e100;
	MatrixXd m(n,n);	
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			m(i,j)=a[i+1][j+1];
	EigenSolver<MatrixXd> es(m,false);
	auto values=es.eigenvalues();
	for(int i=0;i<n;i++)
		mx=max(mx,values[i].real());
	return mx;
}

double rowNorm(auto &a){		//计算无穷范数（行范数）
	double ret=-1;
	for(int i=1;i<=n;i++){
		double t=0;
		for(int j=1;j<=n;j++) t+=abs(a[i][j]);
		ret=max(ret,t);
	}
	return ret;
}

double colNorm(auto &a){		//计算1范数（列范数）
	double ret=-1;
	for(int j=1;j<=n;j++){
		double t=0;
		for(int i=1;i<=n;i++) t+=abs(a[i][j]);
		ret=max(ret,t);
	}
	return ret;
}

double Norm_2(auto &a){		//计算2范数
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) t[j][i]=a[i][j];
	mul(a,t);
	return sqrt(calc(a));
}


int main(){
	srand(time(0));
	puts("input n (2<=n<=20)");
	scanf("%d",&n);
	do{
		flag=false;
		randinit();		//随机生成n阶对称正定矩阵
		det();
	}while(flag);	//确保矩阵非奇异
	init();
	Cholesky(); 		//使用楚列斯基法
	CholeskyAns();
	puts("Cholesky ans is:");	
	out();

	init();
	Cholesky_New();		//改进的楚列斯基法
	CholeskyAns_New();
	puts("Cholesky_New ans is:");
	out();

	//计算条件数
	init();
	double norm_1_num=colNorm(a);	
	double norm_inf_num=rowNorm(a);
	double norm_2_num=Norm_2(a);	
	init();			//计算2范式后会修改a,需要再次初始化
	getReverse(a);
	norm_1_num*=colNorm(a);
	norm_inf_num*=rowNorm(a);
	norm_2_num*=Norm_2(a);
	printf("cond(A)-1 is %lf\n",norm_1_num);	//输出条件数
	printf("cond(A)-2 is %lf\n",norm_2_num);
	printf("cond(A)-inf is %lf\n",norm_inf_num);
}

用简化计算的 $LU$ 分解求 $n$ 阶对角占优不可约的三对角矩阵的时候，也遇到了个小问题：
构建 $n$ 阶对角占优矩阵是很容易的，但如何证明它不可约呢。
查到了这样的一个定理：

n 阶复数方阵 A 是不可约的当且仅当与矩阵 A 对应的有向图 S(A) 是强连通的。

由这个定理易得一个结论：

n阶对角占优矩阵不可约，当且仅当它主对角线、低对角线、高对角线上所有元素非零。

这样就可以生成矩阵了。

由于矩阵是三对角矩阵，开 $n^2$ 的空间是很浪费的，只开 $3n$ 就够用了。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n;
double a[N],b[N],c[N],d[N],e[N],y[N],x[N],f[N];

void randInit(){
	for(int i=1;i<=n;i++){
		f[i]=rand()%200/10.0-10;
		a[i]=rand()%5+1;
		c[i]=rand()%5+1;
		b[i]=a[i]+b[i]+rand()%5+1;
	}
}

void simpleLU(){
	d[1]=c[1]/b[1];
	for(int i=2;i<=n;i++) d[i]=c[i]/(b[i]-a[i]*d[i-1]);		//计算d
	y[1]=f[1]/b[1];	
	for(int i=2;i<=n;i++) y[i]=(f[i]-a[i]*y[i-1])/(b[i]-a[i]*d[i-1]);
	x[n]=y[n];
	for(int i=n-1;i>=1;i--) x[i]=y[i]-d[i]*x[i+1];
}

void out(){
	printf("ans is:\nx = [ ");
	for(int i=1;i<=n;i++) printf("%lf ",x[i]);
	printf("]\n");
}

int main(){
	srand(time(0));
	puts("please input n(1<=n<=1000000):");
	scanf("%d",&n);
	randInit();
	simpleLU();	
	out();
}