目录
递归算法和迭代的定义和说明
递归算法(recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用,在这些语言中函数可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全取代循环,因此在很多函数编程语言(如Scheme)中习惯用递归来实现循环。通俗来说一个过程或函数在其定义或说明时又直接或间接调用自身的一种方法。一般在C语言里递归一般用在定义函数里。
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。迭代算法是用计算机解决问题的一种基本方法,它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值,迭代法又分为精确迭代和近似迭代。比较典型的迭代法如“二分法”和"牛顿迭代法”属于近似迭代法。其实迭代法是由递归出来
?
?
递归算法能够解决的问题
-
数据的定义是按递归定义的。如Fibonacci函数。
-
问题解法按递归算法实现。如Hanoi问题。
-
数据的结构形式是按递归定义的。如二叉树、广义表等。
递归算法例题
下列给定程序中,函数fun()的功能是:应用递归算法求某数a的平方根。求平方根的迭代公式如下:
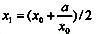
例如,2的平方根为1.414214。(原理就是给一个初始值(比如x0=a/2)迭代求a的平方根,设定一个误差限,不断逼近a)
递归算法:
#include<stdio.h>
#include<math.h>
double fun(double a,double x0)
{ double x1,y;
x1=(x0+a/x0)/2.0;
if(fabs(x1-x0)>=0.00001)
y=fun(a,x1);
else y=x1;
return y;
}
int main()
{double x;
printf("Enter x:");
scanf("%lf",&x);
printf("The square root of %lf is %lf\n",x,fun(x,1.0));
}?迭代法:
include<stdio.h>
#include<math.h>
int main()
{
double x1, x2;
double a;
scanf("%lf",&a);
x2=1.0;
for(;;)
{
x1=x2;
x2=(x1+a/x1)/2.0;
if (fabs(x1 - x2)<0.00001)
{
printf("%.3f",x2);
break;
}
}
return 0 ;
}?总结:
递归是一个树结构,从字面可以其理解为重复“递推”和“回归”的过程,当“递推”到达底部时就会开始“回归”,其过程相当于树的深度优先遍历。
迭代是一个环结构,从初始状态开始,每次迭代都遍历这个环,并更新状态,多次迭代直到到达结束状态。
理论上递归和迭代时间复杂度方面是一样的,但实际应用中(函数调用和函数调用堆栈的开销)递归比迭代效率要低。
从“编程之美”的角度看,可以借用一句非常经典的话:“迭代是人,递归是神!”来从宏观上对二者进行把握。(摘自大佬)
两种方法各有优缺点;