开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> 数据结构C语言—算术表达式求值[栈|中缀表达式法]（采用双顺序栈实现）【2021-12-31】 -> 正文阅读

[C++知识库]数据结构C语言—算术表达式求值[栈|中缀表达式法]（采用双顺序栈实现）【2021-12-31】

数据结构C语言—算术表达式求值[栈|中缀表达式法]（采用双顺序栈实现）【2021-12-31】

一、SbqzDouble.c
二、EvaluateExpression()流程图
三、函数模块清单
三、运行结果示例

【TDTX】
【C99】
【编译与运行环境】64位Windows操作系统，TDM-gcc 4.9.2 64bit编译。
【输入样例】36.8+69-14.5*(25.7-(45.4/2))-3.9#
【注2】采用 中缀表达式法，符合人的直觉。
【注2】采用 float atof(const char* str);函数将数字字符串转为对应的float型的值，再压入OPND栈中。即 实现了多位整数和浮点数表达式的计算。
【问题描述】算术表达式求值问题。
【思路】
1.表达式求值问题中核心问题是实现算符的优先级，使用两个顺序栈分别作为操作数栈和运算符栈的运行工作栈，分别名为： OPND、OPTR。
2.两工作栈的栈底设定为数组 0 位置，栈顶设定为栈顶元素的下一个顺序位置。
【算法思想】
1.首先初始化两个工作栈，其中 OPTR 栈的栈底元素是#，即初始化后立即将#入栈到 OPTR 栈。
2. 依次读入表达式中的字符，是数字字符，将其转化为对应float，当读入到算符字符时先将此float入栈OPND。
3. 若是运算符将 OPTR 栈顶的运算符与当前读入的运算符比较优先级后再执行相应的操作。其中栈顶元素优先级小于读入运算符，将该运算符入栈。
4. 若栈顶元素优先级大于读入运算符，将 OPTR 栈顶元素出栈保存在 theta 中，再让 OPND 出栈两次保存在 a 和 b 中，调用 Operate 函数执行算术运算，结果压入 OPND 中。

一、SbqzDouble.c

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define InitSize 100
#define StepSize 10
#define id_opnd 1
#define id_optr 2
char OP[7] = {'+','-','*','/','(',')','#'};
char tnumber[100];//保存表达式中的数字字符串，用atof函数转为float压入OPND
typedef struct SqStack_OPND
{
	double* base;
	double* top;
	int stacksize;
	int id;
}SqStack_OPND;
typedef struct SqStack_OPTR
{
	char* base;
	char* top;
	int stacksize;
	int id;
}SqStack_OPTR;

int InOP(char* OP,char c)
{
	for(int i = 0;i < 7;i++)
	{
		if(c == OP[i])
		{
			return 1;	
		}	
	}
	return 0;	
} 
int initStack_OPND(SqStack_OPND* S)
{
	S->base = (double*)malloc(sizeof(double)*InitSize);
	if(S->base == NULL)
	{
		S->base = NULL;
		S->top = NULL;
		S->stacksize = -1;
		return 0;
	}
	S->top = S->base;
	S->stacksize = InitSize;
	S->id = id_opnd;
	return 1;
}
int initStack_OPTR(SqStack_OPTR* S)
{
	S->base = (char*)malloc(sizeof(char)*InitSize);
	if(S->base == NULL)
	{
		S->base = NULL;
		S->top = NULL;
		S->stacksize = -1;
		return 0;
	}
	S->top = S->base;
	S->stacksize = InitSize;
	S->id = id_optr;
	return 1;
}
int StackLength(void* s,int id)
{
	if(id == id_opnd)
	{
		SqStack_OPND* S = (SqStack_OPND*)s;
		if(S->base == NULL)
		{
			return -1;
		}
		return S->top-S->base;
	}
	if(id == id_optr)
	{
		SqStack_OPTR* S = (SqStack_OPTR*)s;
		if(S->base == NULL)
		{
			return -1;
		}
		return S->top-S->base;
	}
	return -1;
}
int PushStack_OPND(SqStack_OPND* S,double e)
{
	if(S->base == NULL)
	{
		puts("\nOPND is not exist！");
		return 0;
	}
	if(StackLength(S,S->id) >= S->stacksize)
	{
		S->base = (double*)realloc(S->base,sizeof(double)*(S->stacksize+StepSize));
		if(S->base != NULL)
		{
			S->top = S->base+S->stacksize;
			S->stacksize = S->stacksize+StepSize;
			*(S->top) = e;
			(S->top)++;
			return 1;
		}
		else
		{
			return 0;
		}
	}
	else
	{
		*(S->top) = e;
		(S->top)++;
		return 1;
	}
}
int PushStack_OPTR(SqStack_OPTR* S,char e)
{
	if(S->base == NULL)
	{
		puts("\nOPND is not exist！");
		return 0;
	}
	if(StackLength(S,S->id) >= S->stacksize)
	{
		S->base = (char*)realloc(S->base,sizeof(char)*(S->stacksize+StepSize));
		if(S->base != NULL)
		{
			S->top = S->base+S->stacksize;
			S->stacksize = S->stacksize+StepSize;
			*(S->top) = e;
			(S->top)++;
			return 1;
		}
		else
		{
			return 0;
		}
	}
	else
	{
		*(S->top) = e;
		(S->top)++;
		return 1;
	}
}
int PopStack_OPND(SqStack_OPND* S,double* e)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		return 0;
	}
	else
	{
		(S->top)--;
		*e = *(S->top);
		return 1;
	}
}
int PopStack_OPTR(SqStack_OPTR* S,char* e)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		return 0;
	}
	else
	{
		(S->top)--;
		*e = *(S->top);
		return 1;
	}
}
int GetTopStack_OPND(SqStack_OPND* S,double* e)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		return 0;
	}
	else
	{
		*e = *(S->top - 1);
		return 1;
	}
}
int GetTopStack_OPTR(SqStack_OPTR* S,char* e)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		return 0;
	}
	else
	{
		*e = *(S->top - 1);
		//printf("*e = %c",*e);
		return 1;
	}
}
int TraverseStack_OPND(SqStack_OPND* S)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		printf("栈顶指针----->0：空<-----栈底指针"); 
		return 0;
	}
	double* p;
	printf("栈顶指针----->%d\n",StackLength(S,S->id)); 
	for(p = S->top;p - S->base - 1 != -1;p--)
	{
		if((p - S->base - 1) == 0)
		{
			printf("栈底指针----->0:%f\n",(S->base)[0]);
		}
		else
		{
			printf("              %d:%f\n",p - S->base - 1,(S->base)[p - S->base - 1]);
		}
	}
	return 1;
}
int TraverseStack_OPTR(SqStack_OPTR* S)
{
	if(S->base == NULL)
	{
		return -1;
	}
	if(S->base == S->top)
	{
		printf("栈顶指针----->0：空<-----栈底指针"); 
		return 0;
	}
	char* p;
	printf("栈顶指针----->%d\n",StackLength(S,S->id)); 
	for(p = S->top;p - S->base - 1 != -1;p--)
	{
		if((p - S->base - 1) == 0)
		{
			printf("栈底指针----->0:%c\n",(S->base)[0]);
		}
		else
		{
			printf("              %d:%c\n",p - S->base - 1,(S->base)[p - S->base - 1]);
		}
	}
	return 1;
}
double Operate(double a,char op,double b)
{
	switch(op)
	{
		case '+':return a + b;
		case '-':return a - b;
		case '*':return a*b;
		case '/':
			if(fabs(b-0) <= 0.0000001)
			{
				return -2147483648.2147;
			}
			else
			{
				return a/b; 
			}
		default:return -2147483648.2147;
	}
}
char Precede(char t1,char t2)
{
	switch(t1)
	{
		case '+':
			switch(t2)
			{
				case '+':return '>';
				case '-':return '>';
				case '*':return '<';
				case '/':return '<';
				case '(':return '<';
				case ')':return '>';
				case '#':return '>';
			}
		case '-':
			switch(t2)
			{
				case '+':return '>';
				case '-':return '>';
				case '*':return '<';
				case '/':return '<';
				case '(':return '<';
				case ')':return '>';
				case '#':return '>';
			}
		case '*':
			switch(t2)
			{
				case '+':return '>';
				case '-':return '>';
				case '*':return '>';
				case '/':return '>';
				case '(':return '<';
				case ')':return '>';
				case '#':return '>';
			}
		case '/':
			switch(t2)
			{
				case '+':return '>';
				case '-':return '>';
				case '*':return '>';
				case '/':return '>';
				case '(':return '<';
				case ')':return '>';
				case '#':return '>';
			}
		case '(':
			switch(t2)
			{
				case '+':return '<';
				case '-':return '<';
				case '*':return '<';
				case '/':return '<';
				case '(':return '<';
				case ')':return '=';
				case '#':return '@';
			}
		case ')':
			switch(t2)
			{
				case '+':return '>';
				case '-':return '>';
				case '*':return '>';
				case '/':return '>';
				case '(':return '@';
				case ')':return '>';
				case '#':return '>';
			}
		case '#':
			switch(t2)
			{
				case '+':return '<';
				case '-':return '<';
				case '*':return '<';
				case '/':return '<';
				case '(':return '<';
				case ')':return '@';
				case '#':return '=';
			}	
		default:return '@';
	}
}
double EvaluateExpression()
{
	SqStack_OPND opnd;
	SqStack_OPTR optr;
	
	int n[1] = {0};
	int k = 0;
	char ch;
	char c;
	double pop_a;
	double pop_b;
	char theta;
	char pop_ch;
	double pop_return;
	
	initStack_OPTR(&optr);PushStack_OPTR(&optr,'#');
	initStack_OPND(&opnd);scanf("%c",&c);
	
	while(c != '#' || (GetTopStack_OPTR(&optr,&ch),ch != '#'))  
	{
		if(InOP(OP,c) == 0)
		{
			if((c >= '0' && c <= '9') || c == '.')
			{
				n[0] = 0;
				tnumber[k++] = c;
			}
			//printf("n[0] = %d,n[1] = %d,i-1 = %d\n",n[0],n[1],i-1);
			//PushStack_OPND(&opnd,c-48);
			//TraverseStack_OPND(&opnd);
			//TraverseStack_OPTR(&optr);
			//puts("-------------------");
			c = getchar();
		}
		else
		{
			//printf("[c = %c,n[0] = %d]",c,n[0]);
			if(n[0] == 0)
			{
				tnumber[k] = '\0';
				//PushStack_OPND(&opnd,n[1]);
				PushStack_OPND(&opnd,atof(tnumber));
				n[0] = 1;
				k = 0;
				TraverseStack_OPND(&opnd);
				TraverseStack_OPTR(&optr);
			}

			GetTopStack_OPTR(&optr,&ch);
			switch(Precede(ch,c))
			{
				case '<':
					PushStack_OPTR(&optr,c);
					TraverseStack_OPND(&opnd);
					TraverseStack_OPTR(&optr);
					puts("-------------------");
					c = getchar();
					break;
				case '=':
					PopStack_OPTR(&optr,&pop_ch);
					TraverseStack_OPND(&opnd);
					TraverseStack_OPTR(&optr);
					puts("-------------------");
					c = getchar();
					break;
				case '>':
					PopStack_OPTR(&optr,&theta);
					PopStack_OPND(&opnd,&pop_a);
					PopStack_OPND(&opnd,&pop_b);
					
					if(Operate(pop_b,theta,pop_a) == -2147483648.2147)
					{
						return -2147483648.2147;
					}
					
					PushStack_OPND(&opnd,Operate(pop_b,theta,pop_a));
					TraverseStack_OPND(&opnd);
					TraverseStack_OPTR(&optr);
					puts("-------------------");
					break; 
			}
		}
	}
	GetTopStack_OPND(&opnd,&pop_return);
	free(opnd.base);
	free(optr.base);
	return pop_return;
}
int main()
{
	puts("【输入表达式以#结尾】其中运算符['+','-','*','/','(',')','#']:");
	puts("【参与运算的数字只能是整数或浮点数】"); 
	puts("【例子】：36+69-14*(25-(45/2))-3#"); 
    printf("计算结果：%f\n",EvaluateExpression());
	system("pause");
	return 0;
}

二、EvaluateExpression()流程图

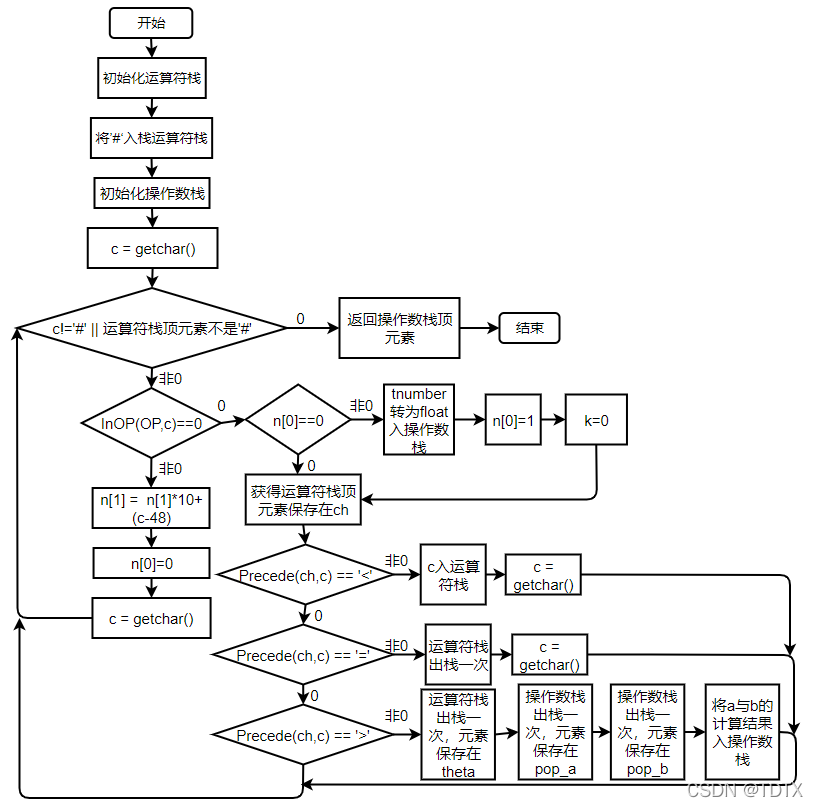
在这里插入图片描述

三、函数模块清单

（1）int InOP(char* OP,char c);
（2）initStack_OPND(SqStack_OPND* S);
（3）initStack_OPTR(SqStack_OPTR* S);
（4）int StackLength(void* s,int id);
（5）int PushStack_OPND(SqStack_OPND* S,double e);
（6）int PushStack_OPTR(SqStack_OPTR* S,char e);
（7) int PopStack_OPND(SqStack_OPND* S,double* e);
（8) int PopStack_OPTR(SqStack_OPTR* S,char* e);
（9) int GetTopStack_OPND(SqStack_OPND* S,double* e);
（10) int GetTopStack_OPTR(SqStack_OPTR* S,char* e);
（11) int TraverseStack_OPND(SqStack_OPND* S);
（12) int TraverseStack_OPTR(SqStack_OPTR* S);
（13) double Operate(double a,char op,double b);
（14) char Precede(char t1,char t2);
（15) double EvaluateExpression();

三、运行结果示例

3.1 36.8+69-14.5*(25.7-(45.4/2))-3.9#

在这里插入图片描述

3.2 36+69-14*(25-(45/2))-3#

在这里插入图片描述

3.3 动态图形式展示结果

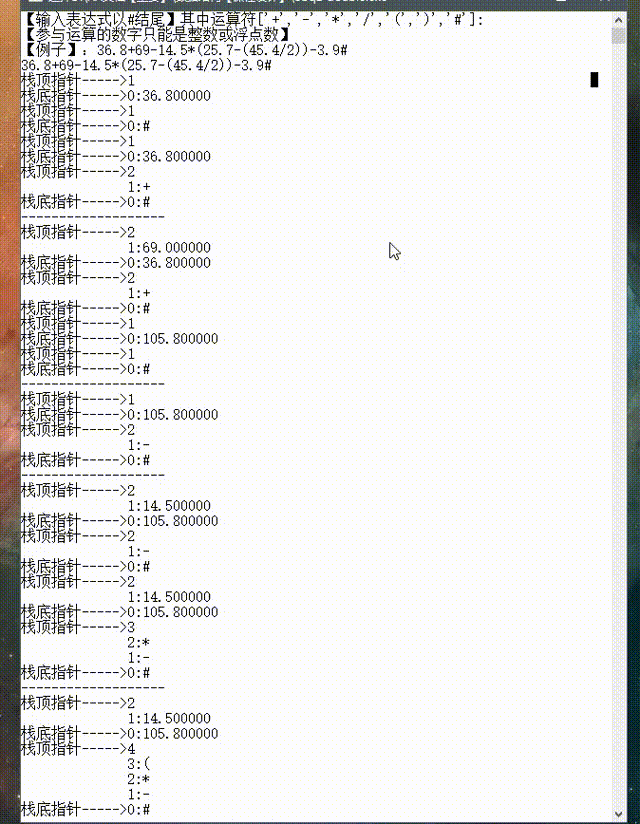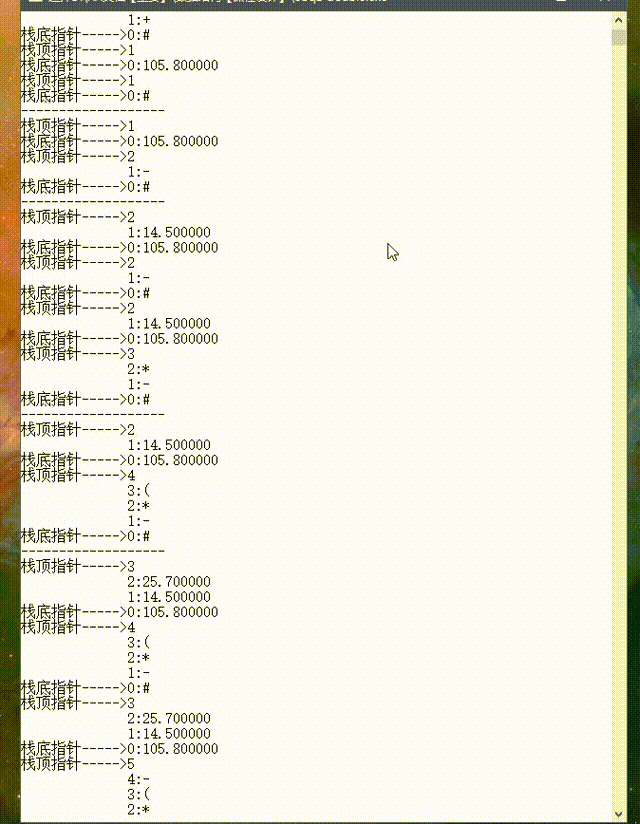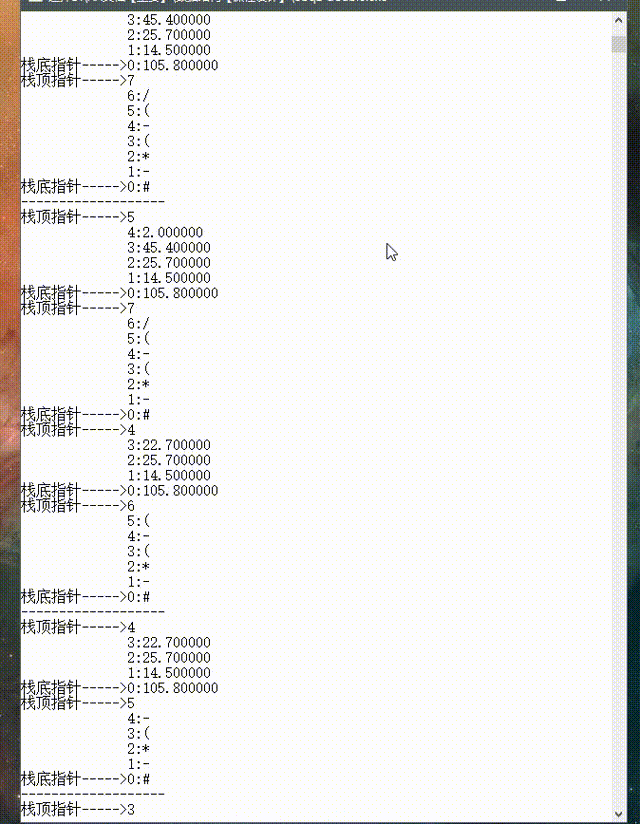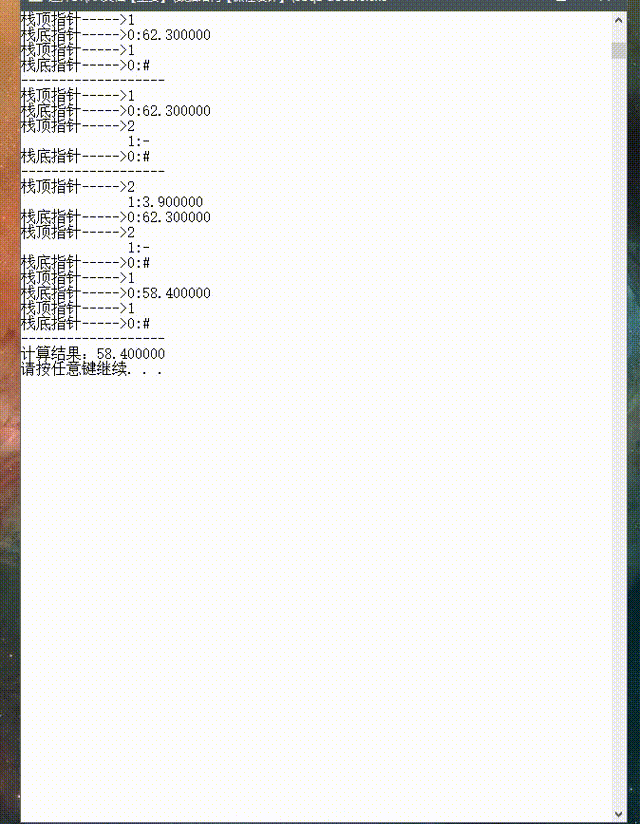
在这里插入图片描述

------------------------------------------------------第九次发文章有点激动啊！-----------------------------------------------------
-----------------------------------------------------【数据结构代码自编练习】------------------------------------------------------
----------------------------------------------------------------【TDTX】-----------------------------------------------------------------