[C++知识库]Codeforces Round #763 (Div. 2) Editorial C 【解题报告】

链接 ：https://codeforces.com/contest/1623/problem/C

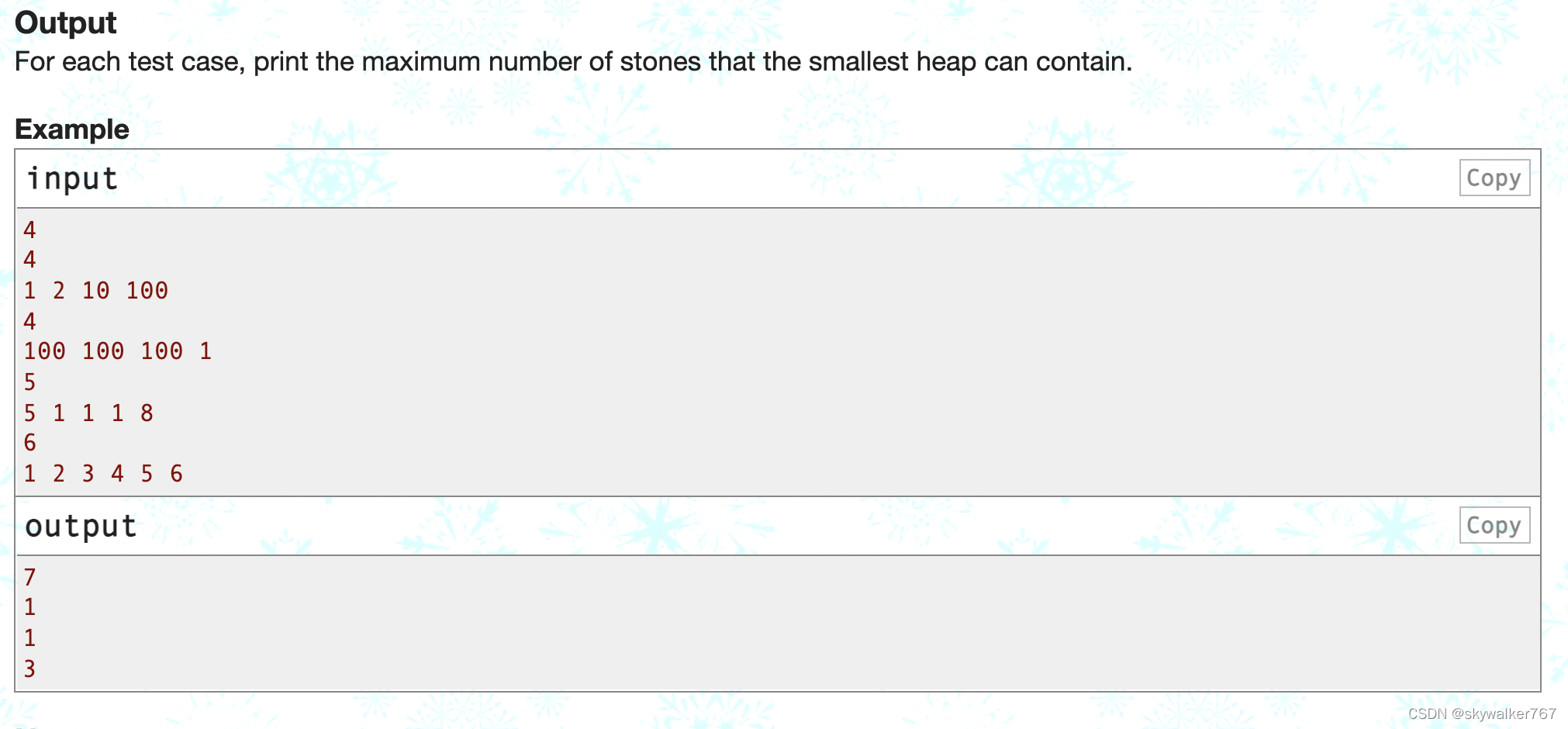
题解： 二分答案即可。比较困扰我的是两个问题：1.怎么求出$d$。2.如何判断这个$mid$的值是否合法。会不会出现，满足check,但是实际上不存在$mid$的情况。

第一个:
$$intd=min(h[i],cu{r}_h[i]?x)/3;$$
被题解的这个$min$折服了，我想的有点复杂的东西，居然可以这样搞。
第二个问题很容易解决，如果不存在，那么要么大，要么小，如果小的话，肯定能二分出更小的地方，如果更大，同理。

#include <bits/stdc++.h>
#define int long long
#define forn(i, n) for (int i = 0; i < n; ++i)
using namespace std;
typedef pair<int , int> PII;
int n;
vector<int> vec;

bool check(int mid)
{
    vector<int> backup(vec.begin() , vec.end());
    for (int i = n - 1;i >= 2;i -- )
    {
        if (backup[i] < mid) return false;
        int d = min(backup[i] - mid , vec[i]) / 3;
        backup[i - 1] += d;
        backup[i - 2] += d * 2;
    }
    return backup[0] >= mid && backup[1] >= mid;
}

signed main()
{
    int T; cin >> T;
    while(T --) {
        cin >> n;
        vec.resize(n);
        forn(i , n) cin >> vec[i];   
        int l = 0 , r = 1e9;
        while(l < r)
        {
            int mid = (l + r + 1) >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1;
        }
        cout << l << endl;
    }
    return 0;
}