汉诺塔问题
#提出问题
有A,B,C三根柱子将A柱子上的的盘子移动到C柱子上,要求:1.每次只能移动一个盘子?2.大盘子不能放到小盘子上
#问题分析
问题一、假如A柱子上有1个盘子:直接将盘子从A柱子移动到C柱子上(移动1个盘子)
问题二、假如A柱子上有2个盘子:1、将A柱子上的盘子移动到B柱子上(移动1个盘子)?2、将A柱子上的盘子移动到C柱子上(移动1个盘子)?3、将B柱子上的盘子移动到C柱子上(移动1个盘子)
问题三、假如A柱子上有3个盘子:1、将A柱子上的盘子移动到B柱子上(移动2个盘子)
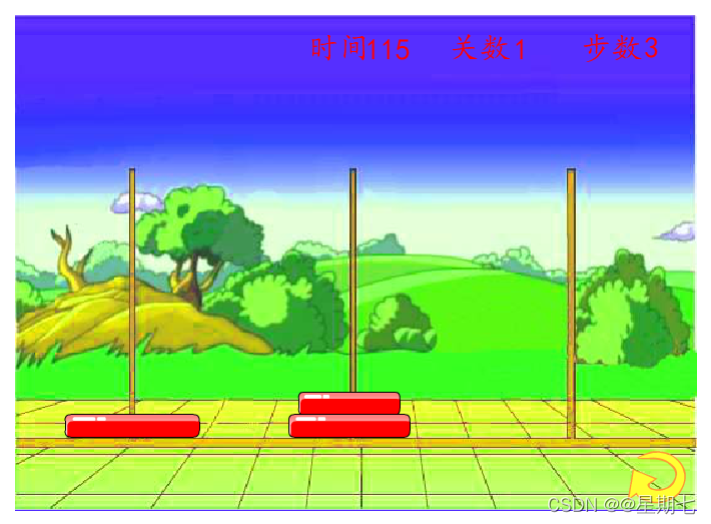
2、将A柱子上的盘子移动到C柱子上(移动1个盘子)

3、将B柱子上的盘子移动到A柱子上(移动2个盘子)
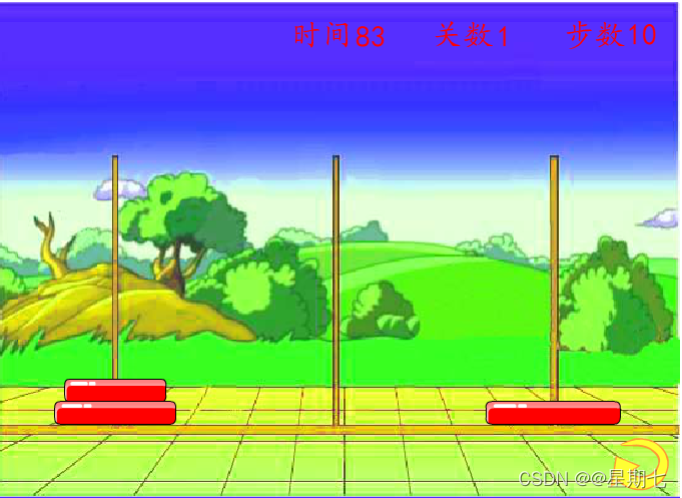
4、将A柱子上的盘子移动到B柱子上(移动1个盘子)

5、将A柱子上的盘子移动到C柱子上(移动1个盘子)
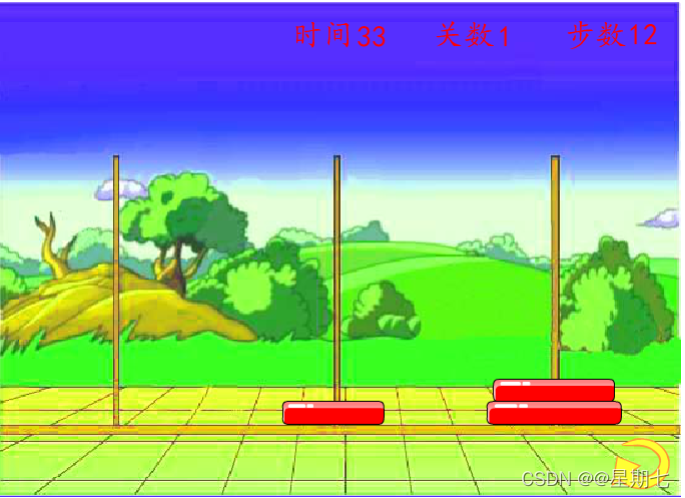
6、将B柱子上的盘子移动到C柱子上(移动1个盘子)

问题四、假如A柱上有四个盘子:(这里步骤就和前面一样,我就只给第一步)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
那么这里面移动两个盘子就有问题了,怎么移动两个盘子呢。实际上从X(X,Y,Z是用来和前面的问题做个区分,防止读者思路被弄乱)柱子移动到Z柱子移动一个盘子我们可以看作是“将盘子从X柱子上借助Y柱子移动到Z柱子上”,那么同理我们移动两个盘子,假如将两个盘子从X柱子上移动到Z柱子上就可以看作是“将两个盘子从X柱子上借助Y盘子移动到Z盘子”这不就可以将这个问题看作是问题二吗;所以我们的递归函数就可以写做move(层数,从X柱子,借助Y柱子,移动到Z柱子);递归函数出口就是:移动的最后一次当层数变为1时,不需要借助其他柱子直接从原来的柱子移动到目标柱子move2(从X柱子,移动到Z柱子);
?
//汉诺塔问题2022.1.28
//A,B,C三个柱子
#include<stdio.h>
void print(char j,char k){ //"j","k",只是代表参数是char类型;
printf("%c -> %c\n",j,k);
}
void move(int n,char x,char y,char z){ //n代表柱子上有n层,从x柱上借助y柱移动到z柱
if(n==1){
print(x,z);
}
else{
move(n-1,x,z,y); //n-1,是每移动一次柱子上的层数减少1;
print(x,z);
move(n-1,y,x,z);
}
}
int main(){
int num;
printf("请输入汉诺塔层数>");
scanf("%d",&num);
move(num,'A','B','C');
return 0;
}
?