链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
?
题目描述
在高为 H 的天花板上有 n 个小球,体积不计,位置分别为 0,1,2,….n-1。在地面上有一个小车(长为 L,高为 K,距原点距离为 S1)。已知小球下落距离计算公式为 d=1/2*g*(t^2),其中 g=10,t 为下落时间。地面上的小车以速度 V 前进。如下图:
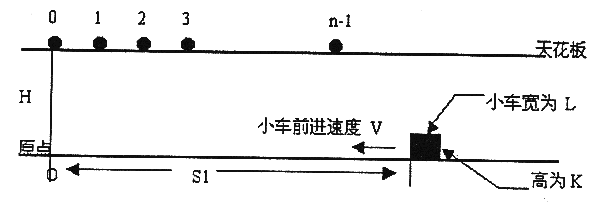
小车与所有小球同时开始运动,当小球距小车的距离 <= 0.00001 时,即认为小球被小车接受(小球落到地面后不能被接受)。
请你计算出小车能接受到多少个小球。
输入描述:
输入H,S1,V,L,K,n (l<=H,S1,V,L,K,n<=100000)
输出描述:
输出小车能接受到的小球个数。
示例1
输入
复制5.0 9.0 5.0 2.5 1.8 5
5.0 9.0 5.0 2.5 1.8 5
输出
复制1
1
个人思路?
? ?这道题我认为属于基础的枚举思想的应用。
? ? 一个物理过程在计算机中模拟,是一个一个“时间片”去处理的,假如我们找出所有时间片的情况来做判断,肯定等找出答案。但是,假如搞出所有“时间片”(比如用t+=0.00001计时)时间复杂度会奇高无比。要化简:真正有用的仅仅是两个特殊的时间点,小车的前端和后端分别在小球正下方时。枚举思想与暴力解决的区别,在于既要不遗漏特殊情况,又要舍弃那些无关的情况。
#include<stdio.h>
double H,S1,V,L,K; int n;
double yBall(double t) //计算小球纵坐标
{
return H - 5*(t*t);
}
double T(double x) //计算小车到某一位置时用的时间
{
return x/V;
}
int main()
{
double t1,t2;
int cnt = 0,i;
scanf("%lf%lf%lf%lf%lf%d",&H,&S1,&V,&L,&K,&n);
for(i=n-1;i>=0;i--)
{
if(S1-i<=0) continue;
t1 = T(S1-i); //小车前端到小球下的时刻
t2 = T(S1+L-i); //小车后端到小球下的时刻
if(yBall(t1)-K<=10e-5&&(yBall(t1)-0)>=-10e-5) //第一种接球:车的前侧面
cnt++;
else if((yBall(t1)-K)*(yBall(t2)-K) <= 0) //第二种接球:车的顶部
cnt++; //类似零点存在定理,一定有yBall>K到yBall<K的过程
//好处是可以无视精度了
}
printf("%d",cnt);
return 0;
}? ? 需要注意一点的是精度的问题。我第一次提交的时候就因此错了部分用例。总结一下方法就是:小于最大的范围,大于最小的范围(如yBall(t1)-0)>= -10e-5 取这个负号)。另外就是像第二种情况的判断条件可以跳过精度的问题,因为double值的符号永远不会有误差。