[C++知识库]2017年第八届蓝桥杯 - 省赛 - C/C++大学A组 - C. 魔方状态

魔方状态

二阶魔方就是只有2层的魔方，只由8个小块组成。

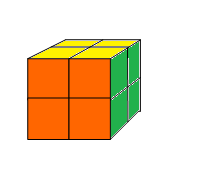
小明很淘气，他只喜欢3种颜色，所有把家里的二阶魔方重新涂了颜色，如下：

前面：橙色
右面：绿色
上面：黄色
左面：绿色
下面：橙色
后面：黄色

请你计算一下，这样的魔方被打乱后，一共有多少种不同的状态。

如果两个状态经过魔方的整体旋转后，各个面的颜色都一致，则认为是同一状态。

请提交表示状态数的整数，不要填写任何多余内容或说明文字。

Ideas

这道题相对来说比较麻烦，而且比赛的时候放在第三题，有点恐怖，建议如果比赛的时候遇到这种填空题，20分钟解决不出来就跳过吧。

如果想要解决这道题，首先面临的第一个问题就是，魔方是三维，我们怎么用计算机语言进行表示。

二阶魔方是由八个块组成的，我们先给这8个块进行编号，上面四个块编号为0_{3，下面四个块编号为4}7。

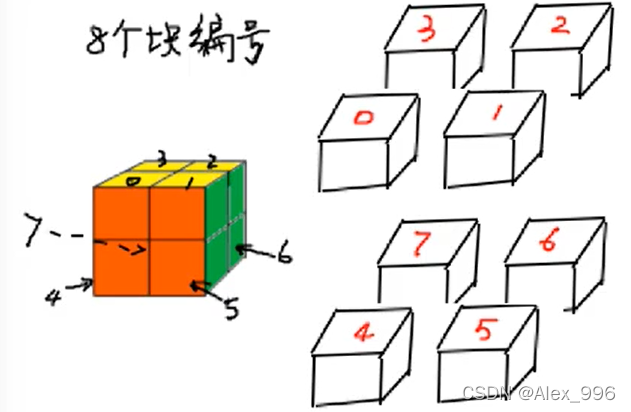
然后对于每一个块，都有六个面，其中有三个面是有颜色，另外三个面在魔方内部，是看不见的，所以我们还要对每一个面进行编号。

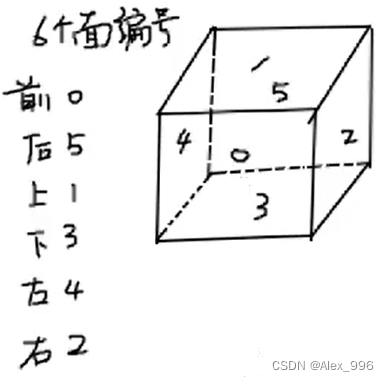
编号为0的块，它的6个面可以表示为['o', 'y', 'x', 'x', 'g', 'x']，其中o表示橙色，y表示黄色，g表示绿色，x表示看不见。

接下来我们就可以用一个二维字符数组表示一个二阶魔方：

cube = [['o', 'y', 'x', 'x', 'g', 'x'],
        ['o', 'y', 'g', 'x', 'x', 'x'],
        ['x', 'y', 'g', 'x', 'x', 'y'],
        ['x', 'y', 'x', 'x', 'g', 'y'],
        ['o', 'x', 'x', 'o', 'g', 'x'],
        ['o', 'x', 'g', 'o', 'x', 'x'],
        ['x', 'x', 'g', 'o', 'x', 'y'],
        ['x', 'x', 'x', 'o', 'g', 'y']]

魔方的状态表示完了之后，接下来就要转动，进行状态转移。

玩过魔方的应该都知道，它的状态转移其实只需要通过三种旋转就可以达到：上面旋转（U）、右面旋转（R）、前面旋转（F）。

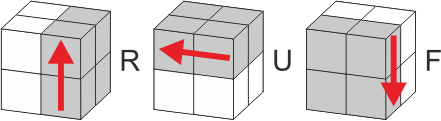
假如对于上面旋转（U）操作，首先0、1、2、3四个块的位置要交换。

0 -> 3
3 -> 2
2 -> 1
1 -> 0

然后每个块的6个面编码也要变换：

0 -> 4
4 -> 5
5 -> 2
2 -> 0

同理我们可以得出剩下两种旋转对应的块和面的变换，这样我们就得到了魔方状态转移的步骤。

接下来我们就要进行搜索了，得到魔方的所有状态。

对于某一种状态，它有R、U、F三种操作，通过每一种操作可以得到一个新的状态，而对于每一种状态，要判断一下之前有没有出现过，如果没有，添加到状态集合中，并且后面要基于这种状态继续搜索。

所以这类似于一个BFS的问题，我们需要通过队列来辅助实现。

另外题目中说“如果两个状态经过魔方的整体旋转后，各个面的颜色都一致，则认为是同一状态”，其实就是我们进行去重的依据，还需要定义一个辅助函数进行魔方的整体旋转。

定义函数try_add，传入一个魔方的状态，然后进行整体旋转操作，同样类似于面的旋转操作，不同的是三个面都要进行整体旋转。

Code

Python

from collections import deque
from copy import deepcopy


def process_cube(state) -> str:
	return ''.join([''.join(x) for x in state])


def u(state):
	# 上面顺时针旋转一次
	
	def u_cell(cell):
		# 上面顺时针旋转一次对应的每个块的面编码变化
		cell[4], cell[5], cell[2], cell[0] = cell[0], cell[4], cell[5], cell[2]
	
	for i in [0, 1, 2, 3]:
		u_cell(state[i])
	
	state[0], state[1], state[2], state[3] = state[1], state[2], state[3], state[0]
	return state


def r(state):
	# 右面顺时针旋转一次
	
	def r_cell(cell):
		# 右面顺时针旋转一次对应的每个块的面编码变化
		cell[0], cell[1], cell[5], cell[3] = cell[3], cell[0], cell[1], cell[5]
	
	for i in [1, 2, 5, 6]:
		r_cell(state[i])
	
	state[1], state[2], state[5], state[6] = state[5], state[1], state[6], state[2]
	return state


def f(state):
	# 前面顺时针旋转一次
	
	def f_cell(cell):
		# 前面顺时针旋转一次对应的每个块的面编码变化
		cell[1], cell[2], cell[3], cell[4] = cell[4], cell[1], cell[2], cell[3]
	
	for i in [0, 1, 4, 5]:
		f_cell(state[i])
	
	state[0], state[1], state[4], state[5] = state[4], state[0], state[5], state[1]
	return state


def u_whole(state):
	# 上+下面顺时针旋转一次
	
	def u_d_cell(cell):
		# 上+下面顺时针旋转一次对应的每个块的面编码变化
		cell[4], cell[5], cell[2], cell[0] = cell[0], cell[4], cell[5], cell[2]
	
	for i in range(8):
		u_d_cell(state[i])
	
	state[0], state[1], state[2], state[3] = state[1], state[2], state[3], state[0]
	state[4], state[5], state[6], state[7] = state[5], state[6], state[7], state[4]
	return state


def r_whole(state):
	# 右+左面顺时针旋转一次
	
	def r_l_cell(cell):
		# 右+左面顺时针旋转一次对应的每个块的面编码变化
		cell[0], cell[1], cell[5], cell[3] = cell[3], cell[0], cell[1], cell[5]
	
	for i in range(8):
		r_l_cell(state[i])
	
	state[1], state[2], state[5], state[6] = state[5], state[1], state[6], state[2]
	state[0], state[3], state[4], state[7] = state[4], state[0], state[7], state[3]
	return state


def f_whole(state):
	# 前+后面顺时针旋转一次
	
	def f_b_cell(cell):
		# 前+后面顺时针旋转一次对应的每个块的面编码变化
		cell[1], cell[2], cell[3], cell[4] = cell[4], cell[1], cell[2], cell[3]
	
	for i in range(8):
		f_b_cell(state[i])
	
	state[0], state[1], state[4], state[5] = state[4], state[0], state[5], state[1]
	state[3], state[2], state[7], state[6] = state[7], state[3], state[6], state[2]
	return state


def try_add(state):
	for _ in range(4):
		state = u_whole(deepcopy(state))
		for _ in range(4):
			state = r_whole(deepcopy(state))
			for _ in range(4):
				state = f_whole(deepcopy(state))
				if process_cube(state) in states:
					return
	states.add(process_cube(state))
	queue.append(state)


if __name__ == '__main__':
	cube = [['o', 'y', 'x', 'x', 'g', 'x'],
	        ['o', 'y', 'g', 'x', 'x', 'x'],
	        ['x', 'y', 'g', 'x', 'x', 'y'],
	        ['x', 'y', 'x', 'x', 'g', 'y'],
	        ['o', 'x', 'x', 'o', 'g', 'x'],
	        ['o', 'x', 'g', 'o', 'x', 'x'],
	        ['x', 'x', 'g', 'o', 'x', 'y'],
	        ['x', 'x', 'x', 'o', 'g', 'y']]
	queue, states = deque(), set()
	queue.append(cube)
	states.add(process_cube(cube))
	while queue:
		front = queue.popleft()
		u_state = u(deepcopy(front))
		try_add(u_state)
		r_state = r(deepcopy(front))
		try_add(r_state)
		f_state = f(deepcopy(front))
		try_add(f_state)
	print(len(states))

Answer: 229878