[C++知识库]【模拟赛】麻煩の雜貨店（单调栈，倍增）

题面

题解

只要转化完题面，我们就完成了大半。

我们将 F 等价为 -1 ，T 等价为 1 ，再求前缀和序列，那么会形成一个无平地的山峰结构：

我们若询问一段区间 $[l,r]$ ，那么便是把 $l$ 左边的山和 $r$ 右边的山都变成深渊，然后在中间下大雨，答案就是最长的平直水面：

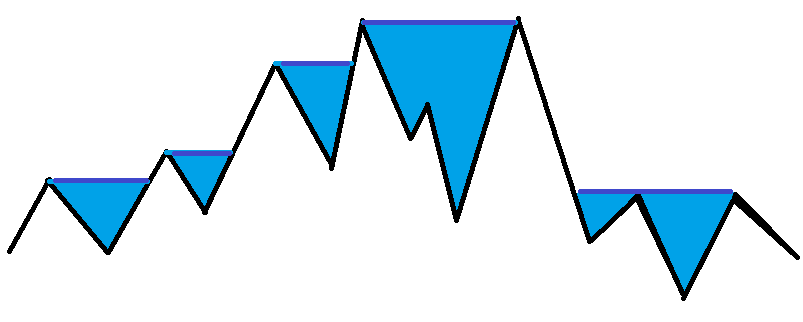
那么我们可以使用单调栈，求出每个点左边第一个严格高于自己的点和右边第一个严格高于自己的点，然后与这两点的距离就是中间水面的长度+1，我们可以依次统计每个水面的长度，求最大值

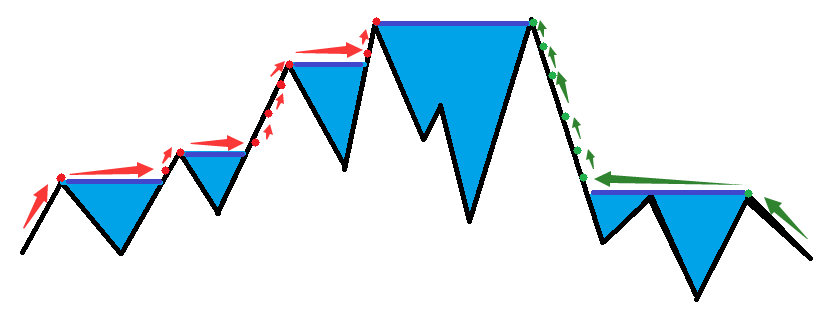
但是水面可能段数极多，因此我们可以倍增处理。我们称一个点走到一个最近的严格更高的点为跳一步，那么预处理出每个点跳 $2_i$ 步的位置以及中间的水面最大值就好。最后会跳到中间的 1~2 个最高点，如果是两个点，如上图，就应该统计这两个点中间的水面。

时间复杂度 $O((n+m)\log n)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 100005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB long double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
//#define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

int n,m,s,o,k;
char ss[MAXN];
int sm[MAXN];
int st[MAXN],tp;
int l[MAXN][20],r[MAXN][20];
int dpl[MAXN][20],dpr[MAXN][20]; // 17
int main() {
	freopen("grocery.in","r",stdin);
	freopen("grocery.out","w",stdout);
	n = read();m = read();
	scanf("%s",ss + 1);
	for(int i = 1;i <= n;i ++) {
		sm[i+1] = sm[i];
		if(ss[i] == 'F') sm[i+1] --;
		else sm[i+1] ++;
	}
	st[tp = 1] = 1;
	for(int i = 2;i <= n+1;i ++) {
		while(tp > 0 && sm[st[tp]] <= sm[i]) tp --;
		if(tp > 0) l[i][0] = st[tp];
		else l[i][0] = 0;
		dpl[i][0] = i - l[i][0] - 1;
		st[++ tp] = i;
	}
	st[tp = 1] = n+1;
	for(int i = n;i > 0;i --) {
		while(tp > 0 && sm[st[tp]] <= sm[i]) tp --;
		if(tp > 0) r[i][0] = st[tp];
		else r[i][0] = 0;
		dpr[i][0] = r[i][0] - i - 1;
		st[++ tp] = i;
	}
	for(int j = 1;j <= 17;j ++) {
		for(int i = 1;i <= n+1;i ++) {
			l[i][j] = l[l[i][j-1]][j-1];
			r[i][j] = r[r[i][j-1]][j-1];
			dpl[i][j] = max(dpl[i][j-1],dpl[l[i][j-1]][j-1]);
			dpr[i][j] = max(dpr[i][j-1],dpr[r[i][j-1]][j-1]);
		}
	}
	while(m --) {
		s = read();o = read()+1;
		int ans = 0;
		for(int i = 17;i >= 0;i --) {
			if(r[s][i] >= s && r[s][i] <= o) {
				ans = max(ans,dpr[s][i]);
				s = r[s][i];
			}
			if(l[o][i] >= s && l[o][i] <= o) {
				ans = max(ans,dpl[o][i]);
				o = l[o][i];
			}
		}
		ans = max(ans,o-s);
		AIput(ans,'\n');
	}
	return 0;
}