题目:输出“魔方阵”。所谓魔方阵是指这样的方阵,它的每一行、每一-列和对角线之和均相等。例如,三阶魔方阵为
8 1 6
3 5 7
4 9 2
要求输出1 ~ n的自然数构成的魔方阵。
魔方阵中各数的排列规律如下:
(1)将1放在第1行中间一列。
(2) 从2开始直到n×n止各数依次按下列规则存放:每一个数存放的行比前一个数的行数减1,列数加1(例如上面的三阶魔方阵,5 在4的上一行后一列)。
(3)如果上一数的行数为1,则下一个数的行数为n(指最下一行)。例如,1在第1行,则⒉应放在最下一行,列数同样加1。
(4) 当上一个数的列数为n时,下一个数的列数应为1,行数减1。例如,2在第3行最后一列,则3应放在第2行第1列。
(5) 如果按上面规则确定的位置上已有数,或上一个数是第1行第n列时,则把下一个数放在上一个数的下面。例如,按上面的规定,4应该放在第1行第2列,但该位置已被1占据,所以4就放在3的下面.由于6是第1行第3列(即最后一列),故7放在6下面。
按此方法可以得到任何阶的魔方阵。
C语言代码实现:
#include<stdio.h>
#define N 3 // 在这里通过改变N的值实现对阶数的控制,注意N只能是奇数
int main(void){
int array[N][N]; // 声明一个N阶二维数组
int i, j, k;
// 二维数组赋初值都为0
for(i = 0; i < N; i++){
for(j = 0; j < N; j++){
array[i][j] = 0;
}
}
// 找到1存放的位置
i = 0;
j = N/2;
array[i][j] = 1;
// 从2 ~ N*N一次添加到矩阵中
for(k = 2; k <= N*N; k++){
i = i - 1; // 行减1
j = j + 1; // 列加1
if((i < 0) && (j == N)){ // 如果上一个元素为第一行第N列,则放在下一个元素的下面
i = i + 2;
j = j - 1;
}else{
if(i < 0) i = N - 1; // 如果上一个元素是第一行,则下个元素在最后一行
if(j == N) j = 0; // 如果上一个元素是第一列,则下个元素在第一列
}
if(array[i][j] == 0){ // 如果二维数组array[i][j]的位置未被占用,则把k赋值到 array[i][j]
array[i][j] = k;
}else{ // 如果二维数组array[i][j]位置已经被占用,则把k放在上一个位置的下面
i = i + 2;
j = j -1;
array[i][j] = k;
}
}
// 打印魔方阵
for(i = 0; i < N; i++){
for(j = 0; j < N; j++){
printf("%5d", array[i][j]);
}
printf("\n");
}
return 0;
}
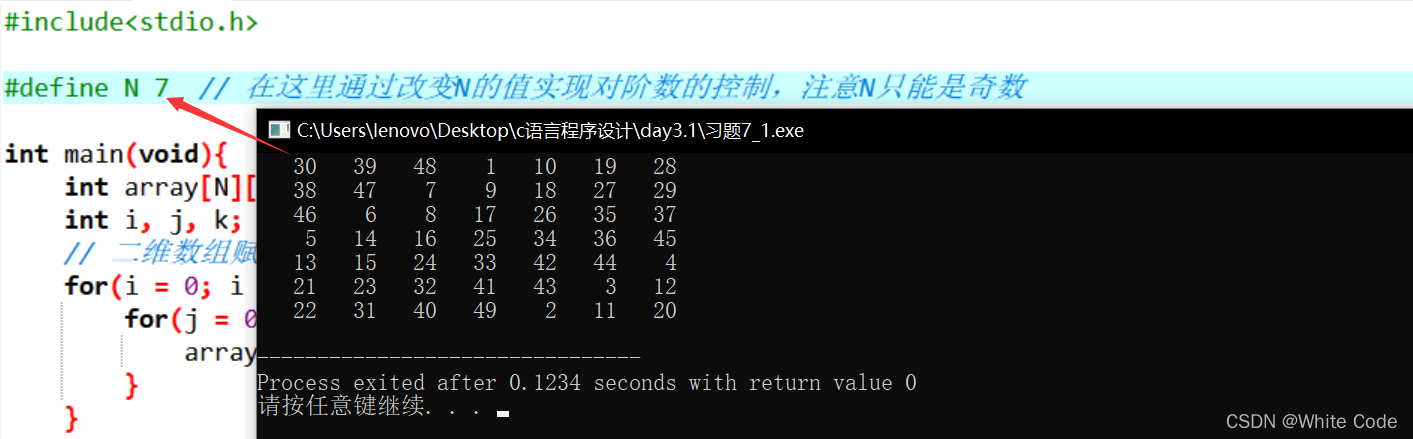
3阶魔方阵截图:
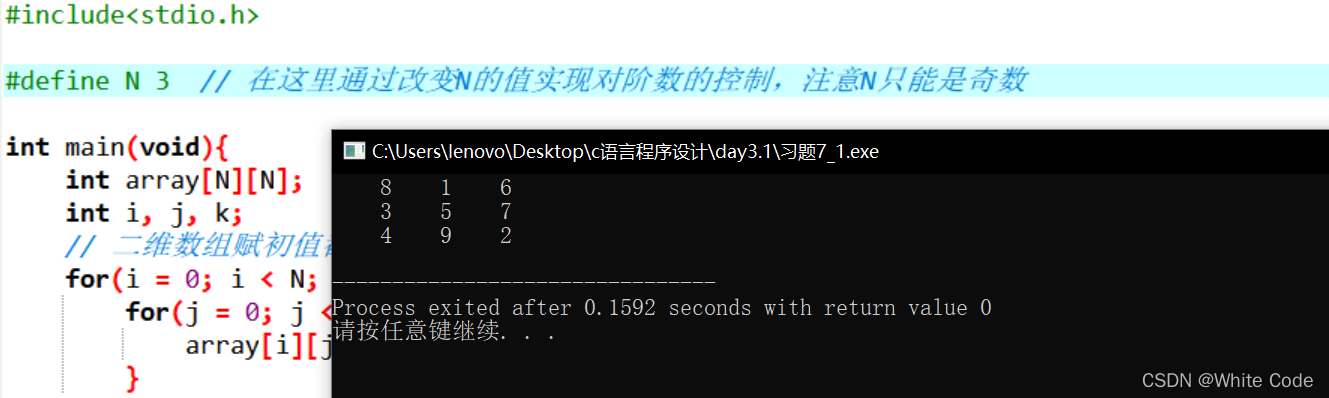
5阶魔方阵截图:
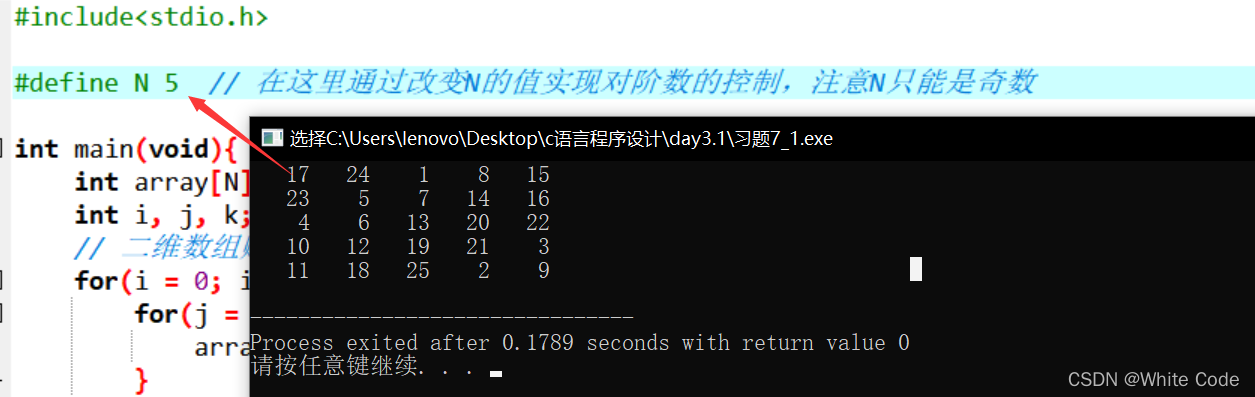
7阶魔方阵截图: