[C++知识库]【洛谷】P1057 [NOIP2008 普及组] 传球游戏

原题链接

P1057 [NOIP2008 普及组] 传球游戏

解题思路

题目数据范围不算小，暴力肯定会超时，这时候我们想到DP

从找规律开始。
我们可以发现，任何一个位置都只能从左边和右边传过来，那么他只能从他左边和他右边的同学手上接到球，所以球传到他手上的路径数等于球传到他左边同学的路径数与球传到他右边同学的路径数之和。
这样我们就可以列出我们的方程：
f[i][j]=f[i-1][j-1]+f[i-1][j+1]

推导过程：
假设有5个人，传6次球
在初始情况下，小蛮手中必然有且只有一个球，记为1；
第一轮传球后，小蛮必然将手中的球传给2号或5号同学，于是这两个同学各有1种方式接到球；
第二轮传球后，（如果上一轮小蛮将球传给2号）2号同学必然将球传给小蛮或3号，（如果上一轮小蛮将球传给5号），5号同学必然将球传给小蛮或4号，于是小蛮有2种情况接到球（分别从2号和5号手中）；
第三轮及其后以此类推。

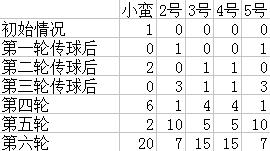
我们据图可以发现，假设初始情况为第0行，小蛮为第1列，则有（从第1行开始）：
f[i][j]=f[i-1][j-1]+f[i-1][j+1];
在加上1和n的特判。
结束。

AC代码

#include<iostream>
using namespace std;
int m, n;
int f[31][31];
int main() {
	cin >> n >> m;
	f[0][1] = 1;
	for(int i = 1; i <= m; i++) {
		for(int j = 1; j <= n; j++) {
			if(j == 1)
				f[i][j] = f[i - 1][n] + f[i - 1][2];
			else if(j == n)
				f[i][j] = f[i - 1][1] + f[i -1 ][n - 1];
			else
				f[i][j] = f[i - 1][j - 1] + f[i - 1][j + 1];
		}
	}
	cout << f[m][1] << endl;
	return 0;
}