开学第一次比赛!有很多原题,但是有一些寒假没处理完的东西,,,
B - Nuts
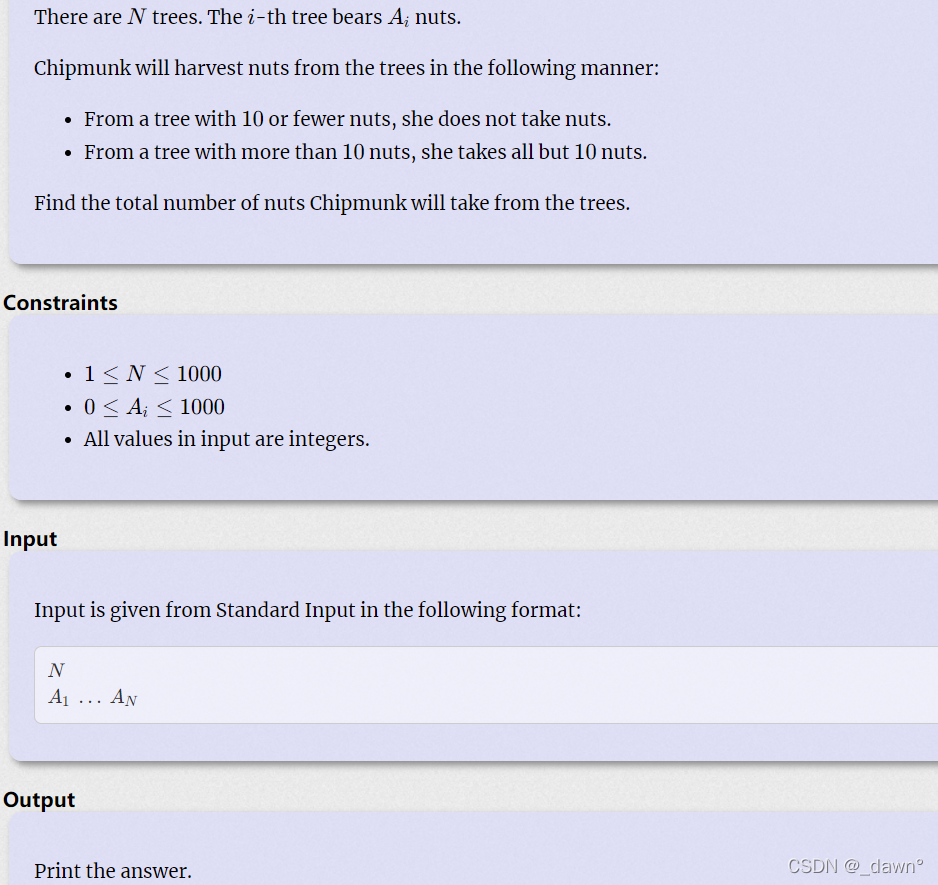
计算数组中每个数大于10的和。
思路:遍历数组相加,不会爆int。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
const int N=1e3+5;
int n;
int a[N];
int ans;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]>10)
ans+=(a[i]-10);
}
cout<<ans<<'\n';
return 0;
}
D - Tour
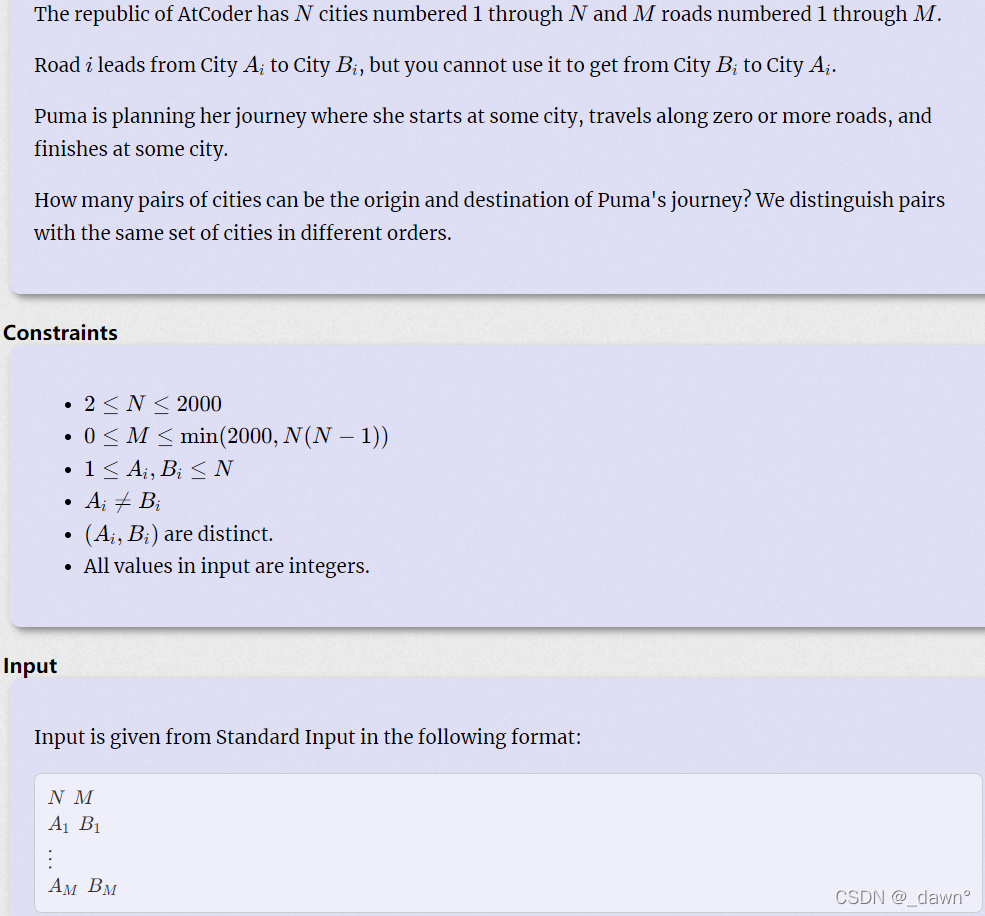
给出n个城市,m条单向道路,问可以作为起点和终点的城市组有几对。
思路:链式前向星存图,DFS对每一个点搜索。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
const int N=2e3+5;
int n,m;
int ver[N],nex[N],head[N],cnt;
bool vis[N];
void add_edge(int u,int v)
{
ver[++cnt]=v;
nex[cnt]=head[u];
head[u]=cnt;
}
void dfs(int x)
{
vis[x]=true;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
add_edge(u,v);
}
int ans=0;
for(int i=1;i<=n;i++)
{
for(int i=1;i<=n;i++)
vis[i]=false;
dfs(i);
for(int i=1;i<=n;i++)
ans+=vis[i];
}
cout<<ans<<'\n';
return 0;
}
os:dfs还是不行啊,简简单单一个题用了将近两个小时wwwwww,多练习多练习?
F?- Rock-paper-scissors
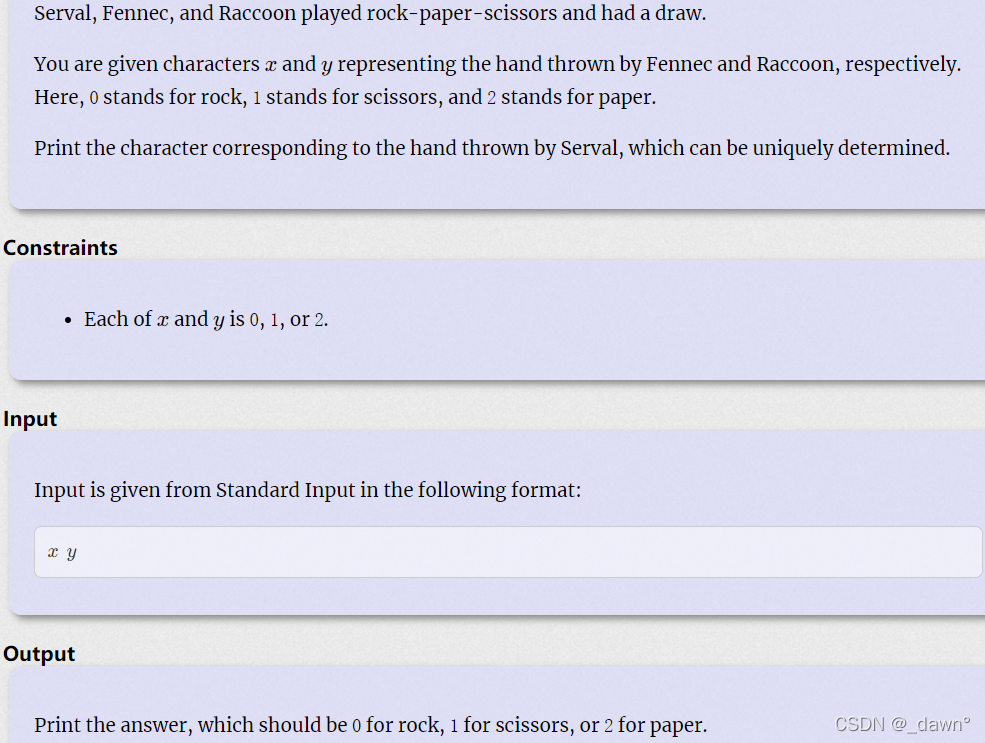
三人剪子包袱锤打成平局,给出其中两个人的选择,问第三个人的选择。
思路: 若两人选择相同,则第三个人也相同;若不同,则第三个人选择剩下的一个。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
int x,y;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>x>>y;
if(x==y) cout<<x<<'\n';
else cout<<3-x-y<<'\n';
return 0;
}
G -?Roping the Field

 ?给出多个点的坐标,是每一个栅栏的坐标,还有多个怪圈的圆心坐标及半径,用绳索连接栅栏,但是绳索不能穿过怪圈,且绳索之间不能相交,问可以连接多少条。
?给出多个点的坐标,是每一个栅栏的坐标,还有多个怪圈的圆心坐标及半径,用绳索连接栅栏,但是绳索不能穿过怪圈,且绳索之间不能相交,问可以连接多少条。
思路:看题意像是一个几何题。先考虑怎样不连接怪圈上的绳索。即怪圈圆心到每一条绳索的最短距离要大于半径,那么就是预处理点到线段距离,之前的题里有一个涉及到的。剩下的就要求怎样连接可以连接最多,即DP问题,则考虑区间DP。区间DP部分不算难写,但是主要是预处理部分要考虑,最后就是要满足不能交叉。
AC代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
#define ept 1e-6
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
const int N=200;
double R;
int n,m;
int f[N][N];
bool vis[N][N];
struct node
{
double x,y;
} a[N],b[N];
double len(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double distance(node u,node v,node w)
{
double cc=0;
double a,b,c;
a=len(u,v);
b=len(v,w);
c=len(u,w);
if(c<=ept||b<=ept)
{
cc=0;
return cc;
}
if(a<=ept)
{
cc=b;
return cc;
}
if(c*c>=a*a+b*b)
{
cc=b;
return cc;
}
if(b*b>=a*a+c*c)
{
cc=c;
return cc;
}
double p=(a+b+c)/2;
double s=sqrt(p*(p-a)*(p-b)*(p-c));
cc=2*s/a;
return cc;
}
bool judge(node a,node b,node c)
{
double dd=distance(a,b,c);
if(dd>R) return 0;
return 1;
}
bool check(node u,node v)
{
for(int i=1;i<=m;i++)
{
if(judge(u,v,b[i]))
return 0;
}
return 1;
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n>>m>>R;
for(int i=1;i<=n;i++)
cin>>a[i].x>>a[i].y;
for(int i=1;i<=m;i++)
cin>>b[i].x>>b[i].y;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j) continue;
vis[i][j]=check(a[i],a[j]);//预处理二维矩阵,即按照怪圈有几条可以连接
}
}
for(int l=3;l<=n;l++)//区间长度最小为3
{
for(int i=1;i<=n-l+1;i++)
{
for(int j=i;j<=i+l-1;j++)//j为区间间断点
{
f[i][i+l-1]=max(f[i][i+l-1],f[i][j]+f[j][i+l-1]);
}
if(vis[i][i+l-1]&&(i!=1||i+l-1!=n))
f[i][i+l-1]++;//更新每个区间的值
}
}
cout<<f[1][n]<<'\n';
return 0;
}
H - Cooking
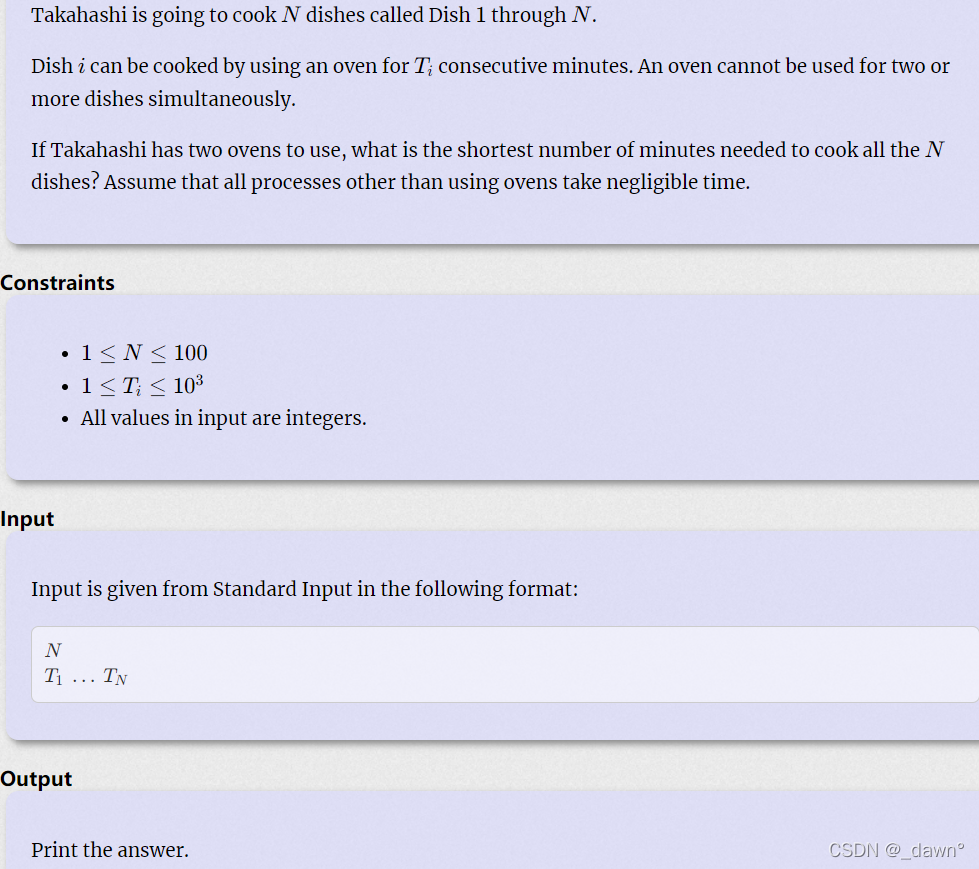
有多个菜品需要不同时间完成,现在有两个烤箱,问最少需要多长时间。
思路:01背包问题,背包上限是所有菜品时间相加除以二。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
const int N=105;
int n;
int t[N],ans;
int f[1000005];
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>t[i];
ans+=t[i];
}
for(int i=1;i<=n;i++)
{
for(int j=ans/2;j>=t[i];j--)
{
if(j>=t[i])
f[j]=max(f[j],f[j-t[i]]+t[i]);
}
}
cout<<ans-f[ans/2]<<'\n';
return 0;
}
os:寒假题里印象比较深的一道,,,
J?- Rush Hour 2
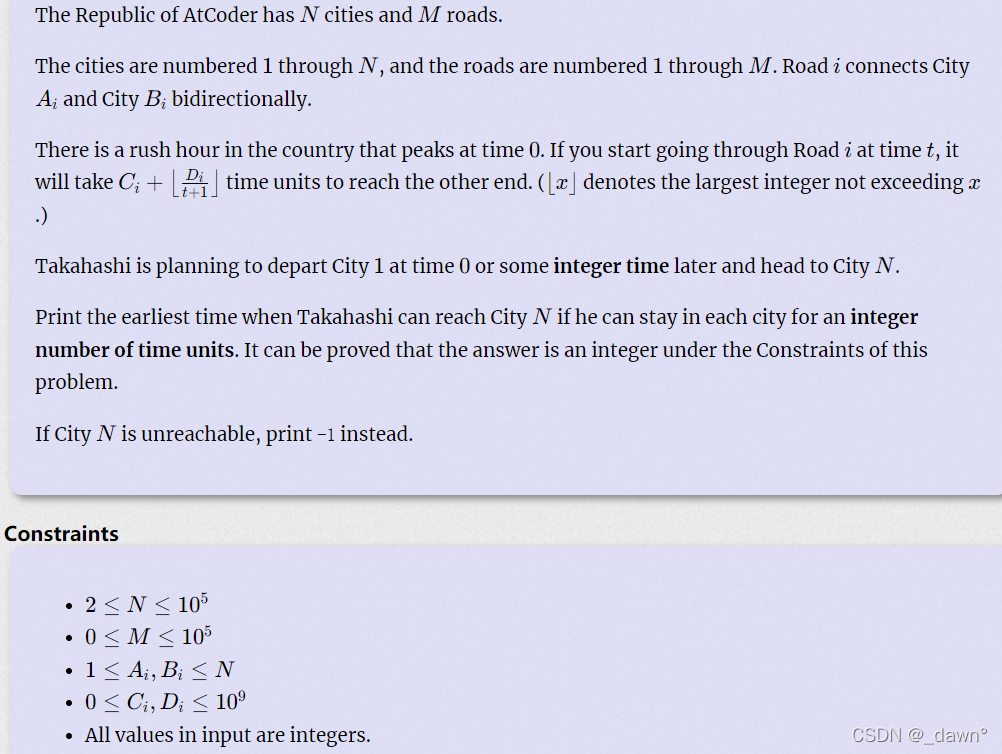
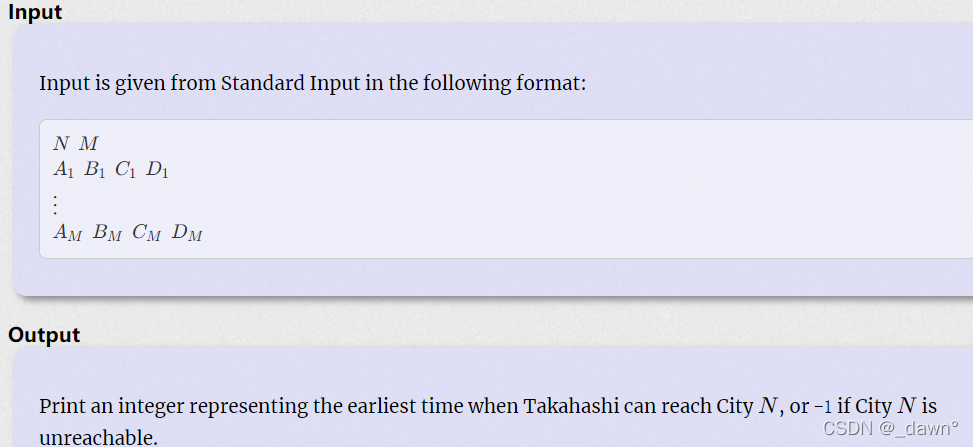
给定四个数,由A到B,所用时间为C,因为traffic jam,还需要一个时间是,t是离开时间,问1~N的最短时间。
思路:可以看出是最短路问题,但是时间需要注意,因为给了时间相关的方程,所以要选择时间最短的行走。我们可以根据均值不等式a+b>=2*sqrt(a*b),得出当t=sqrt(D)-1时出发用时最短,所以当到达时间小于这个时,可以等到该时间再走;若到达时间大于该点,则直接走因为数据范围较大,用链式前向星存图。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f3f3f3f3f
//判断是否需要开ll!!!
//判断是否需要初始化!!!
const int mod=1e9+7;
const ll N=1e5+5;
ll n,m,a,b,c2,d2;
ll to[N<<1],c[N<<1],d[N<<1],nex[N<<1],head[N],vis[N<<1];
ll dis[N<<1],cnt;
void add_edge(ll a,ll b,ll c1,ll d1)
{
to[++cnt]=b;
c[cnt]=c1;
d[cnt]=d1;
nex[cnt]=head[a];
head[a]=cnt;
}
void Dijkstra(){
fill(dis,dis+(N<<1),INF);
dis[1]=0;
priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>>q;
q.push({0,1});
while(q.size())
{
pair<ll,ll>p=q.top();
q.pop();
if(vis[p.second]) continue;
vis[p.second]=1;
for(ll i=head[p.second];i;i=nex[i])
{
ll best=INF;
ll j=to[i];
ll x=(ll)sqrt(1.0*d[i]);
ll L=max(dis[p.second],x),R=x;
R=max(R,L);
for(ll t=L;t<=R;t++){
ll s=t+c[i]+d[i]/(t+1);
best=min(best,s);
}
if(dis[j]>best){
dis[j]=best;
q.push({best,j});
}
}
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
//ios;
cin>>n>>m;
for(ll i=0;i<m;i++)
{
cin>>a>>b>>c2>>d2;
add_edge(a,b,c2,d2);
add_edge(b,a,c2,d2);
}
Dijkstra();
if(dis[n]==INF) cout<<-1<<'\n';
else cout<<dis[n]<<'\n';
return 0;
}