[C++知识库]蓝桥杯试题--九宫重排

题目概述

方法一 单向bfs

九宫重排问题就是典型的广度优先搜索问题，最初我的想法是利用单向的广度优先搜索实现，利用set来查重，通过广度优先搜索保证所需的步骤是最快的(关键点)。但是问题是单向的bfs速度上较慢，我在某些oj上运行不能通过，所以去查资料，发现还可以使用第二种方法。

方法二 双向bfs

单向虽然可以，但是速度比双向慢。因为随着递归的深度变深，每走一步要尝试更多种走法，双向bfs利用的就是两边同时走，在方向不同但是图案相同的点相遇。

借用别人的图来说明一下

?

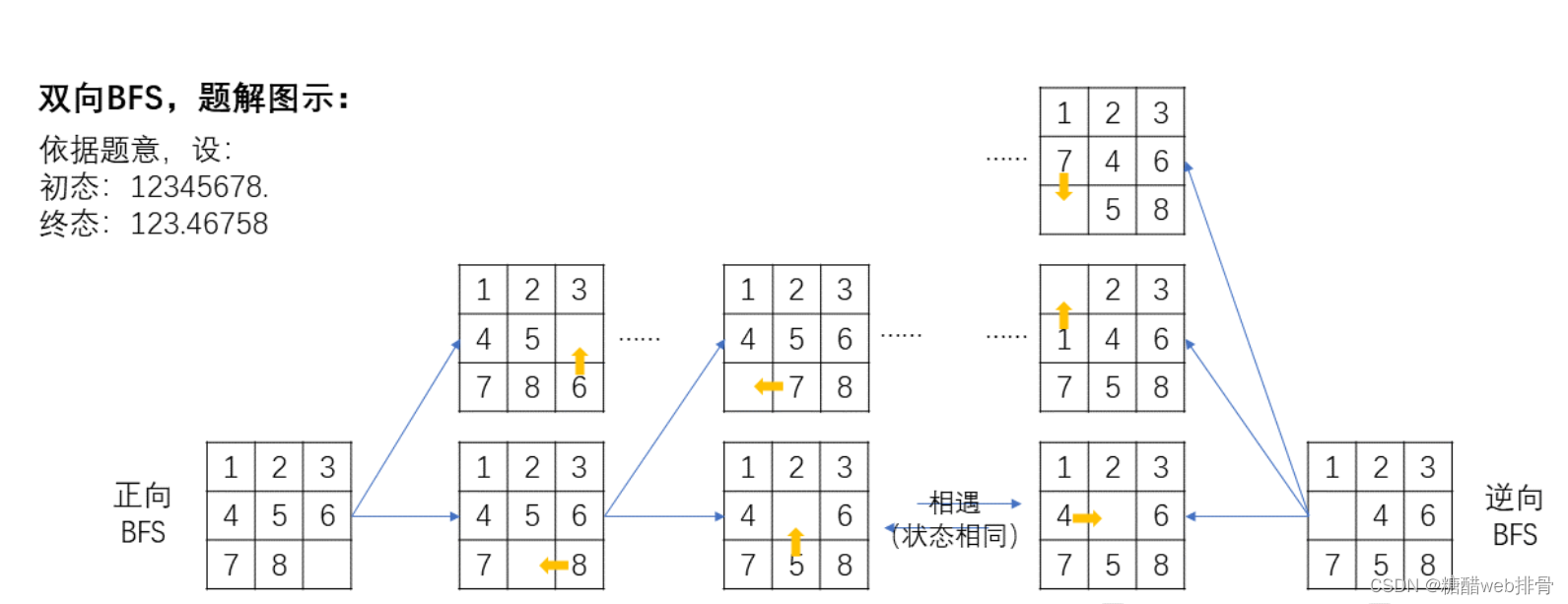
代码如下

#include<iostream>
using namespace std;
#include<map>
#include<queue>

int dx[4] = { 0, 1, 0, -1 }, dy[4] = { -1, 0, 1, 0 };
string nextMat(string mat, int dir) {
    int dotInd = mat.find('.');
    int sucX = dotInd / 3 + dx[dir], sucY = dotInd % 3 + dy[dir];
    if (sucX < 0 || sucY < 0 || sucX>2 || sucY>2) return "null";
    swap(mat[dotInd], mat[(sucX * 3) + sucY]);
    return mat;
}

int bfs(string first, string endd)
{
    queue<string> Q;
    Q.push(first);
    Q.push(endd);
    map<string, int> thestep;
    map<string, int> thedirect;
    thestep[first] = 0; thestep[endd] = 0;
    thedirect[first] = 1; thedirect[endd] = 2;
    while (!Q.empty())
    {
        string str = Q.front();
        Q.pop();
        for (int i = 0; i < 4; i++)
        {
            string tempstr = nextMat(str, i);
            if (tempstr != "null" && thedirect[tempstr] != thedirect[str])
            {
                if (thedirect[tempstr] + thedirect[str] == 3)
                {
                    return thestep[tempstr] + thestep[str] + 1;
                }
                Q.push(tempstr);
                thedirect[tempstr] = thedirect[str];
                thestep[tempstr] = thestep[str] + 1;
            }

        }
    }
    return -1;
}

int main()
{
    string first, endd;
    cin >> first;
    cin >> endd;
    cout << bfs(first, endd);
}