[C++知识库]数三角形 LibreOJ - 2240

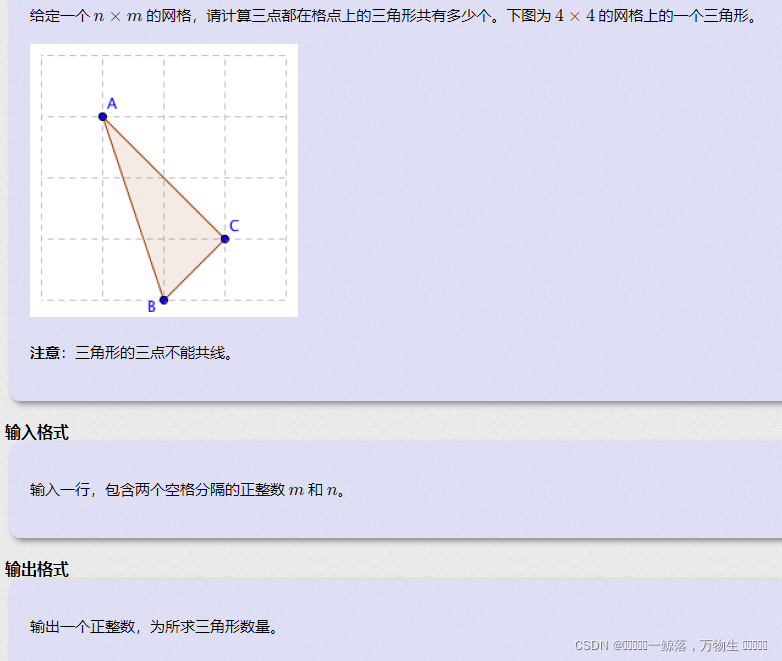
解题思路：首先算出取点的所有可能的情况，先让m++,n++,所有可能的情况是C(mn,3)，然后我们就可以采用容斥原理的思路，将所有不符合的情况去掉，那什么是不符合的情况来？由于构成的三角形的3个点各不相同，只有当3点共线时才不会构成三角形，这时我们可以将三点共线的情况分斜率来考虑：
1、斜率不存在，即竖直情况，mC(n,3)
2、斜率为0，即水平情况，nC(m,3)
3、斜率存在且不为0，共分正负2中情况，但正负是对称的，所以只需要考虑一种情况即可，这里拿斜率大于0的情况来讨论：
（1）、首先我们来枚举底为j，高为i的直角三角形，这样的的三角形共有(n-i)(m-j)种（我们这里只考虑的斜率大于0的情况）。
（2）、对于每个直角三角形，其斜边上的2个端点一定是共线的，现在的任务是找到在直角三角形斜边是上可以有多少个整数点（不包括两个端点），这里应该是gcd(i,j)-1，具体为啥是这个结果，可以看我的上一篇博客。
总结：对于第3种情况，每一个底为j，高为i的直角三角形可以构成的三点共线的种数是（gcd(i,j)-1)(n-i)(m-j)*2。
上代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int n,m;
int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
long long c(long long n)
{
    return (long long)n*(n-1)*(n-2)/6;
}
int main()
{
    cin>>n>>m;
    n++;
    m++;
    long long res=c(m*n)-n*c(m)-m*c(n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        res-=(long long)(gcd(i,j)-1)*(n-i)*(m-j)*2;
    cout<<res<<endl;
    return 0;
}