A. 合数个数(5 分)
答案:1713
试题 A: 合数个数(5 分)
【问题描述】
一个数如果除了 1 和自己还有其他约数,则称为一个合数。例如:1, 2, 3不是合数,4, 6 是合数。
请问从 1 到 2020 一共有多少个合数。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
1~2020共有2020个数,因此我们只要求出素数的个数,结果便是2020-素数个数。
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e4+10;
const int mod=998244353;
int ans=2020;
bool is_prime(int x){
for(int i=2;i*i<=x;i++){
if(x%i==0) return false;
}
return true;
}
int main(){
iostream::sync_with_stdio(false);
int n=2020;
for(int i=1;i<=n;i++){
if(is_prime(i)) ans--;
}
cout<<ans<<endl;
return 0;
}
B.含 2 天数(5 分)
答案:1994240
试题 B: 含 2 天数(5 分)
【问题描述】
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴,因为每天日历上都可以看到 2。
如果日历中只显示年月日,请问从公元 1900 年 1 月 1 日到公元 9999 年 12月 31 日,一共有多少天日历上包含 2。即有多少天中年月日的数位中包含数字2。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
简单模拟。
只需要枚举1900年1月1号到9999年12月31日的每一天,判断该天的时期是否包含2;若包含,则结果加1.
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e4+10;
const int mod=998244353;
int yue[15]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int ans=0;
bool is_run(int x){
if(x%400==0||(x%4==0&&x%100!=0)) return true;
return false;
}
bool f(int x){
while(x){
if(x%10==2) return true;
x/=10;
}
return false;
}
bool check(int x,int y,int z){
if(f(x)||f(y)||f(z)) return true;
return false;
}
int main(){
iostream::sync_with_stdio(false);
for(int i=1900;i<=9999;i++){
if(is_run(i)) yue[2]=29;
else yue[2]=28;
for(int j=1;j<=12;j++){
for(int k=1;k<=yue[j];k++){
if(check(i,j,k)) ans++;
}
}
}
cout<<ans<<endl;
return 0;
}
C.本质上升序列(10 分)
答案:3616159
试题 C: 本质上升序列(10 分)
【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
线性dp。 我们定义状态f[i]表示以字符s[i]结尾的本质不同的方案数。显然,这样定义状态是没有后效性的,因为f[i]不会涉及到第i个字符之后的字符。那么状态如何转移呢?首先可以发现,第i个字符的状态只会和前i-1个字符有关;因此我们需要枚举前i-1个字符;
- 当前i-1个字符中有某个字符j和s[i]相同时,那么这里会出现重复的方案;但是由于f[i]是一定已经包含了f[j]的,所以我们为了避免重复,可以令f[j]=0。
- 当前i-1个字符中有某个字符j小于s[i]时,那么f[i]+=f[j]。因为s[i]>s[j],所以可以继承f[j]的所有方案。
- 当前i-1个字符中有某个字符j大于s[i]时,那么跳过即可。
最后结果便是f[1]+f[2]+…+f[200]。
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e4+10;
const int mod=998244353;
char s[maxn];
LL f[maxn],ans=0; //f[i]表示以s[i]结尾的本质不同的方案数
int main(){
int n; cin>>n;
for(int i=1;i<=n;i++) cin>>s[i];
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++){
if(s[i]==s[j]) f[i]=0;
else if(s[j]<s[i]) f[i]+=f[j];
}
}
for(int i=1;i<=n;i++) ans+=f[i];
cout<<ans<<endl;
return 0;
}
D.咫尺天涯(10 分)
答案:
试题 D: 咫尺天涯(10 分)
【问题描述】
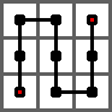
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形,它是从左下角出发,经过一个 3 × 3 的方格中的每一个格子,最终到达右上角的一条曲线。
设每个格子的边长为 1,在上图中,有的相邻的方格(四相邻)在皮亚诺曲线中也是相邻的,在皮亚诺曲线上的距离是 1,有的相邻的方格在皮亚诺曲线中不相邻,距离大于 1。
例如,正中间方格的上下两格都与它在皮亚诺曲线上相邻,距离为 1,左右两格都与它在皮亚诺曲线上不相邻,距离为 3。
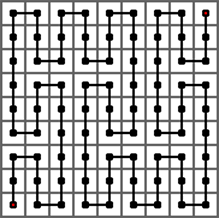
下图给出了皮亚诺曲线的 2 阶情形,它是经过一个3^2× 3 ^2 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
下图给出了皮亚诺曲线的 3 阶情形,它是经过一个 3^3 × 3 ^3 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。
皮亚诺曲线总是从左下角开始出发,最终到达右上角。
小蓝对于相邻的方格在皮亚诺曲线上的相邻关系很好奇,他想知道相邻的方格在曲线上的距离之和是多少。
例如,对于 1 阶皮亚诺曲线,距离和是 24,有 8 对相邻的方格距离为 1, 2 对相邻的方格距离为 3,2 对相邻的方格距离为 5。
再如,对于 2 阶皮亚诺曲线,距离和是 816。请求出对于 12 阶皮亚诺曲线,距离和是多少。
提示:答案不超过 10^18。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
E.玩具蛇(15 分)
答案:552
试题 E: 玩具蛇(15 分)
【问题描述】
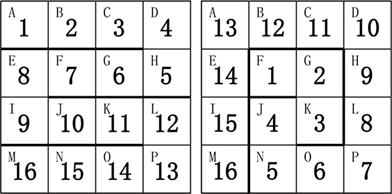
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
dfs。 要是能理解题意,就是模板题。由于数字1的位置有16种情况,所以我们需要枚举每一种情况进行dfs()。
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e4+10;
const int mod=998244353;
int ans=0,vis[5][5];
int dx[5]={0,-1,0,1,0};
int dy[5]={0,0,1,0,-1};
void dfs(int x,int y,int k){
if(k==16){
ans++; return ;
}
for(int i=1;i<=4;i++){
int tx=x+dx[i],ty=y+dy[i];
if(tx>=1&&tx<=4&&ty<=4&&ty>=1&&!vis[tx][ty]){
vis[tx][ty]=1;
dfs(tx,ty,k+1);
vis[tx][ty]=0;
}
}
}
int main(){
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
vis[i][j]=1;
dfs(i,j,1);
vis[i][j]=0;
}
}
cout<<ans<<endl;
return 0;
}
F.皮亚诺曲线距离(15 分)



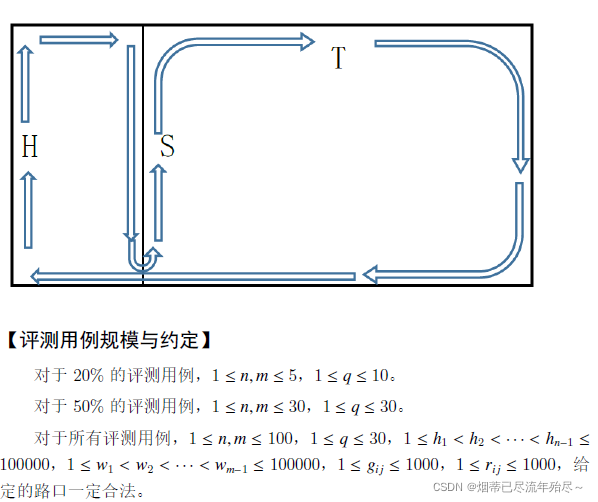
G.出租车(20分)



H.答疑(20分)


思路:
贪心。 我们要求让每个同学发信息的时刻和最小,我们可以发现一定的规律。首先,每个同学的s[i]+a[i]一定是在最后结果里的;因为每个同学都需要完成进入办公室和问完问题以后才能发信息;然后第2个同学的开始时间便是第一个同学的结束时刻,即s[1]+a[1]+e[1];第3个同学的开始时间便是第2个同学的结束时刻,即s[1]+s[2]+a[1]+a[2]+e[1]+e[2];…;第n个同学的开始时间便是第n-1个同学的结束时刻,即s[1]+s[2]+…+s[n-1]+a[1]+a[2]+…+a[n-1]+e[1]+e[2]+…+e[n-1];我们将每个同学用的所有时间s[i]+a[i]+e[i]记为num[i];那么很显然规律便是num[1]加了n-1次,num[2]加了n-2次,…,num[n-1]加了1次;所以我们只需要把num[1~n]排好序,便可以求出结果。
注意:结果要开long long
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e3+10;
int n;
LL sum=0;
int s[maxn],a[maxn],e[maxn],num[maxn];
int main(){
iostream::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i]>>a[i]>>e[i];
sum+=s[i]+a[i];
num[i]=a[i]+s[i]+e[i];
}
sort(num+1,num+1+n);
for(int i=1;i<n;i++) sum+=(n-i)*num[i];
cout<<sum<<endl;
return 0;
}
I.奇偶覆盖(25分)


思路:
暴力骗40分。 一个样例规模,有40%的样例n<=1000;l,r,b,t<=100;显然可以直接暴力;枚举每一个矩形;再遍历该矩形的每一个面积为1的小方格;将其标记值a[i][j]+1;标记值a[i][j]表明第i行第j列的小矩形被覆盖的次数。
时间复杂度:O(n*max(l,r)*max(b,t))
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e4+10;
int n,a[maxn][maxn];
LL ji=0,ou=0;
int main(){
iostream::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
int l,b,r,t;
cin>>l>>b>>r>>t;
for(int j=l+1;j<=r;j++){
for(int k=b+1;k<=t;k++)
a[j][k]+=1;
}
}
for(int i=1;i<=1000;i++){
for(int j=1;j<=1000;j++){
if(a[i][j]==0) continue;
if(a[i][j]&1) ji++;
else ou++;
}
}
cout<<ji<<endl<<ou<<endl;
return 0;
}
J.蓝跳跳(25分)


思路:
动态规划+暴力。 我们用数组f[i][j]表示状态:蓝跳跳跳到了位置 i 且已经 j 次连续跳跃距离超过p。 显然这样定义状态以后结果便是f[L][0]+f[L][1]。 既然状态已经有了,那是怎么转移呢?显然由于蓝跳跳一步可以跳距离1~k;所以位置i处的状态与i-k,i-k+1,…,i-1有关 ;显然;我们可以枚举可能跳跃的距离1~k;此时由于跳跃距离可能小于p,也可能大于p;我能需要分类讨论:
- 当跳跃距离小于p时;此时f[i][0]+=f[i-j][0]+f[i-j][1]。
- 当跳跃距离大于等于p时,此时f[i][1]+=f[i-j][0]。
注意:每次进行加运算都需要mod20201114以防结果溢出。 由于该dp时间复杂度是O(L*k),所以只能拿30分。。。。
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18
typedef long long LL;
const int maxn=1e3+10;
const int mod=20201114;
LL ans=0,k,p,L;
LL f[maxn][3]; //f[i][j]表示在位置i上并且已经连续出现了j次大于p的方案数
int main(){
iostream::sync_with_stdio(false);
cin>>k>>p>>L;
f[0][0]=1;
for(int i=1;i<=L;i++){
for(int j=1;j<=k&&j<=i;j++){
if(j<p) f[i][0]=(f[i][0]%mod+f[i-j][0]%mod+f[i-j][1]%mod)%mod;
else f[i][1]=(f[i][1]%mod+f[i-j][0]%mod)%mod;
}
}
cout<<(f[L][0]+f[L][1])%mod<<endl;
return 0;
}