
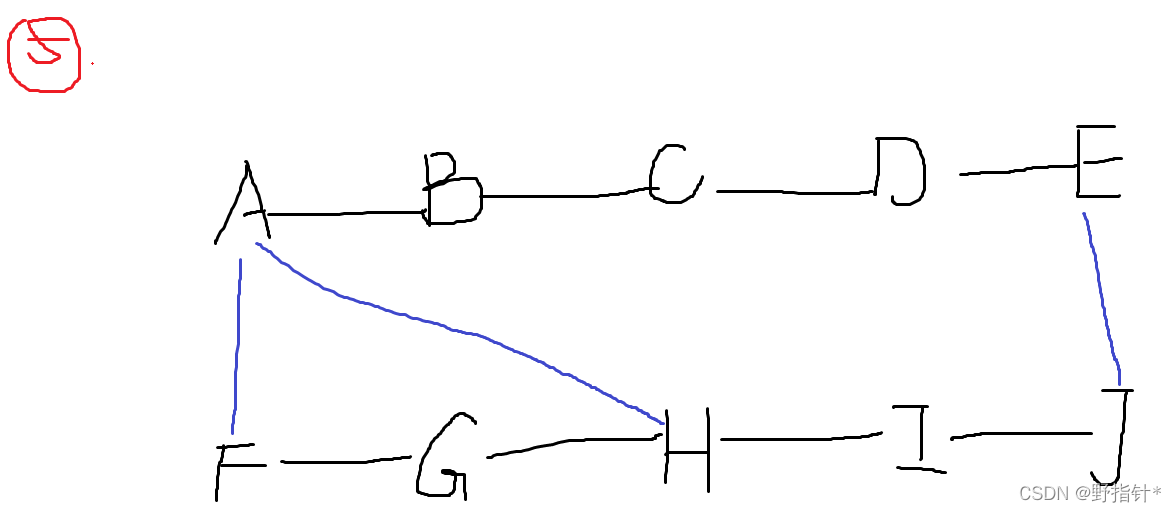
给定两行节点,相邻的节点连一条边,成为两条链,现要求在两条链之间连线,使得任意一个节点被破坏后都不会把整个连通块划分成两份或者更多份.
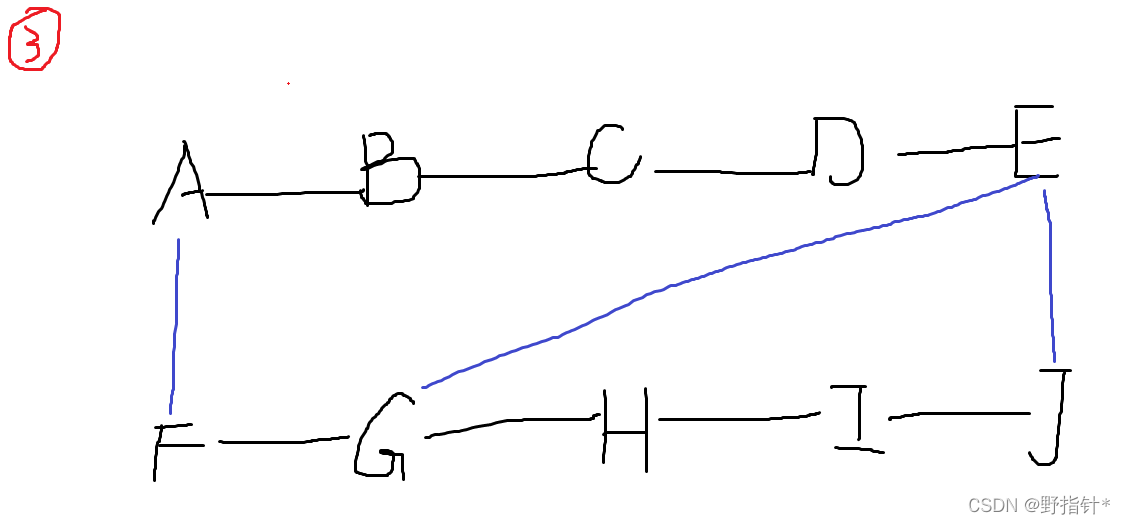
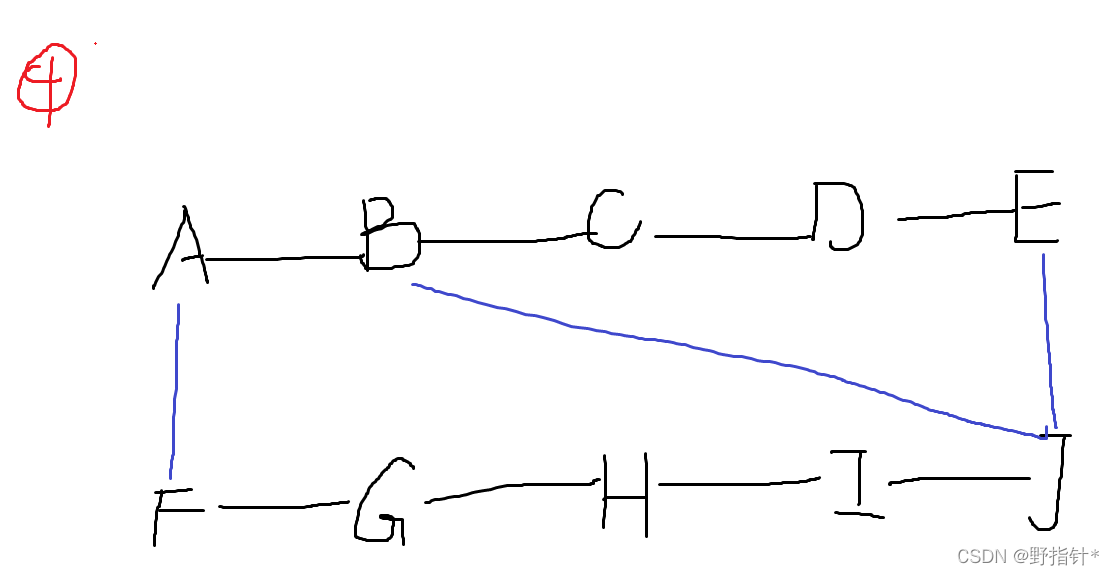
我们注意到:对于两条链,两端一定要连线.而且最多只能连4条线,最少连2条线.
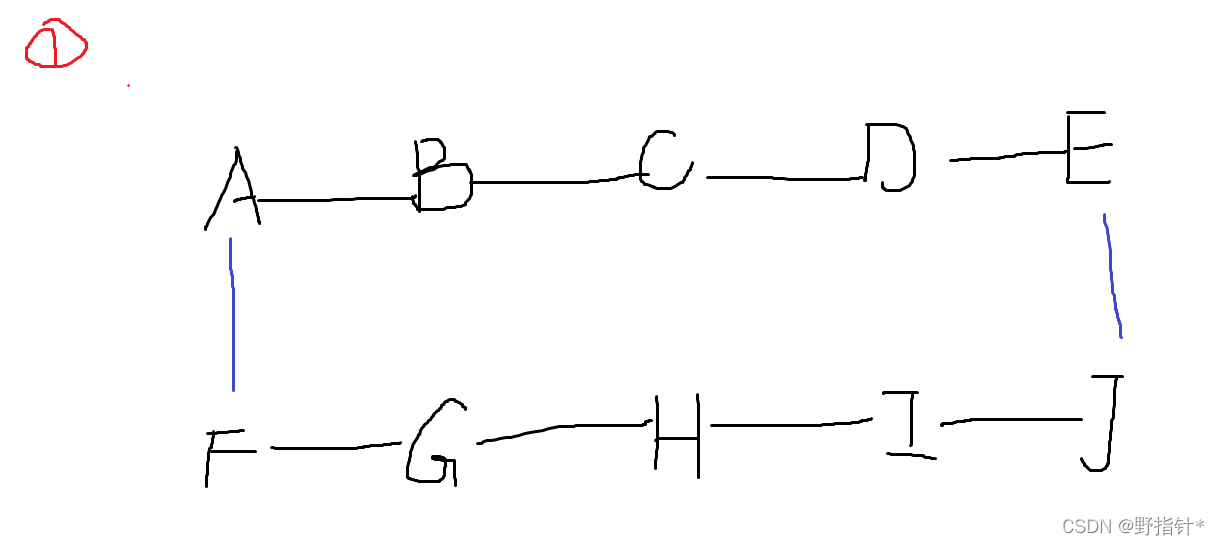
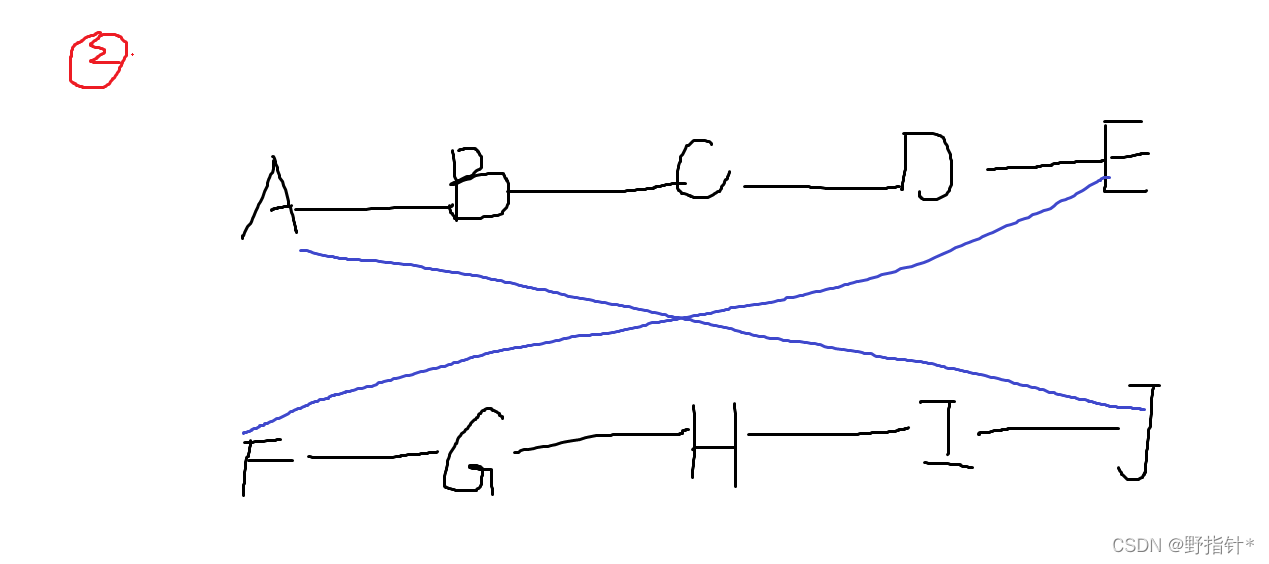
?
?
?
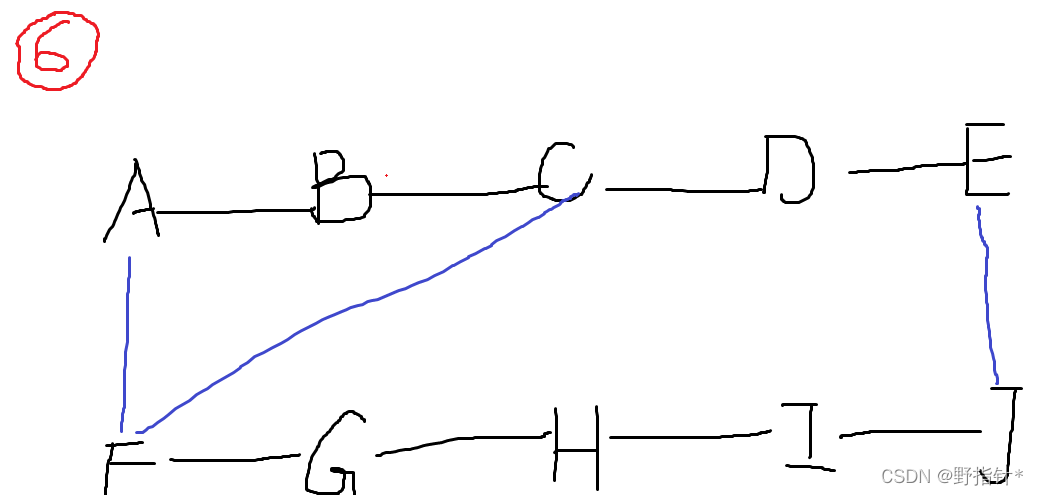
?
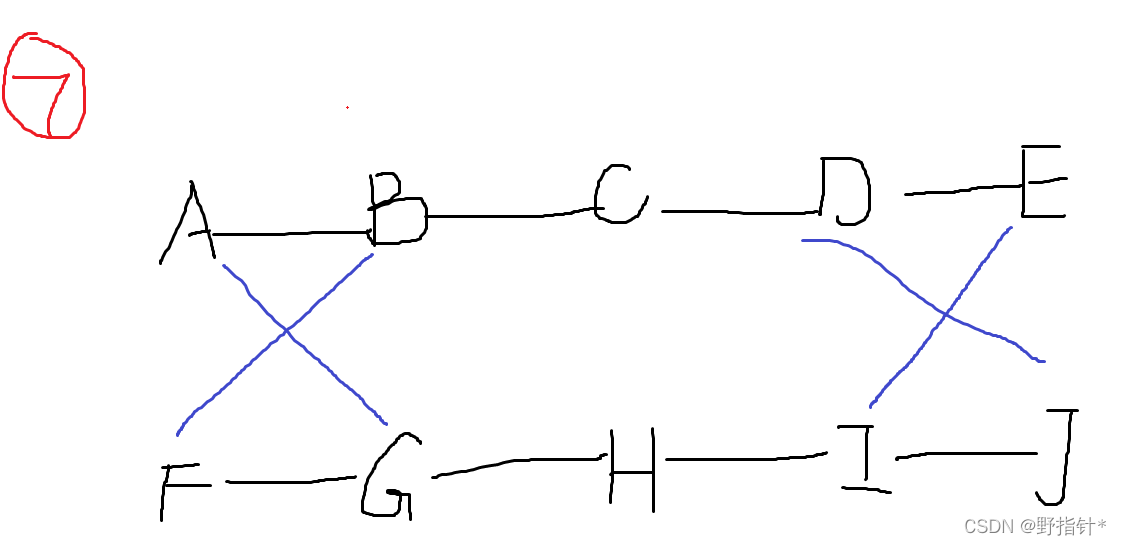
?
?代码如下:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int INF = 1e9;
signed main () {
ios::sync_with_stdio(0); cin.tie(0);
int tt;
cin >> tt;
while (tt--) {
int n;
cin >> n;
vector<int> a(n), b(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
for (int i = 0; i < n; i++) {
cin >> b[i];
}
int ans = min(abs(a[0] - b[0]) + abs(a[n - 1] - b[n - 1]), abs(a[0] - b[n - 1]) + abs(a[n - 1] - b[0]));
int d[4] = {INF, INF, INF, INF};
for (int x : b) {
d[0] = min(d[0], abs(x - a[0]));
d[1] = min(d[1], abs(x - a[n-1]));
}
for (int x : a) {
d[2] = min(d[2], abs(x - b[0]));
d[3] = min(d[3], abs(x - b[n - 1]));
}
ans = min(ans, abs(a[0] - b[0]) + d[1] + d[3]);
ans = min(ans, abs(a[n - 1] - b[n - 1]) + d[0] + d[2]);
ans = min(ans, abs(a[n - 1] - b[0]) + d[0] + d[3]);
ans = min(ans, abs(a[0] - b[n - 1]) + d[1] + d[2]);
ans = min(ans, d[0] + d[1] + d[2] + d[3]);
cout << ans << '\n';
}
}
给定n个互异的点,求出每个点最近的不是已给定的点的坐标.最近指的是曼哈顿距离
我们先暴力解决这个问题,对每个点bfs即可.但是这样会超时,我们可以利用其他已知点的最近点得到该点的距离最近的坐标.
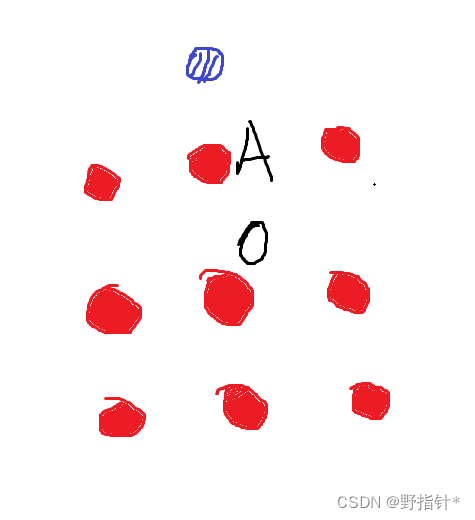
?在上面的例子中,我们可以用A的答案来更新O的答案
我们首先建立一个队列,遍历所有的点,如果该点周围没有被占满,那么就更新答案,放入队列中.
然后对这个队列进行拓展,更新其他点的答案.
代码如下:
#include <bits/stdc++.h>
// #define LOCAL
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(false), cin.tie(0)
#define int long long
#define debug(a) cerr << #a << "=" << a << endl;
using namespace std;
const int N = 2e5 + 5;
const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
map<pair<int, int>, int> mp;
pair<int, int> cor[N];
queue<int> q;
int d[N], ansx[N], ansy[N];
void solve(){
int n;
cin >> n;
for (int i = 0, x, y; i < n; ++i){
cin >> x >> y;
cor[i] = {x, y};
mp[{x, y}] = i;
}
for (int i = 0; i < n; ++i)
for (int j = 0; j < 4; ++j){
int x = cor[i].first + dx[j], y = cor[i].second + dy[j];
if(!mp.count({x, y})){
d[i] = 1;
ansx[i] = x, ansy[i] = y;
q.emplace(i);
}
}
while(q.size()){
int now = q.front();
q.pop();
for (int i = 0; i < 4; ++i){
int x = cor[now].first + dx[i], y = cor[now].second + dy[i];
if(mp.count({x, y})){
if(d[mp[{x, y}]])
continue;
d[mp[{x, y}]] = d[now] + 1;
ansx[mp[{x, y}]] = ansx[now];
ansy[mp[{x, y}]] = ansy[now];
q.emplace(mp[{x, y}]);
}
}
}
for (int i = 0; i < n; ++i)
cout << ansx[i] << ' ' << ansy[i] << '\n';
}
signed main(){
#ifdef LOCAL
freopen("input.in", "r", stdin);
freopen("output.out", "w", stdout);
#endif
IOS;
int tt = 1;
while (tt--)
solve();
}