D. Madoka and the Best School in Russia
一道思维题,基本思路是把x的因子全部提取出来,比如有n个,就看成n个盒子,然后剩余数字设为y,考虑把y拆分放到n个盒子中。(注意:相同集合,不同顺序算作同一种情况)
但是还有一种特殊操作,如果因子d是合数,还能考虑再把d拆分,和y一起放到剩下n-1个盒子中。
情况比较多,要分类讨论。
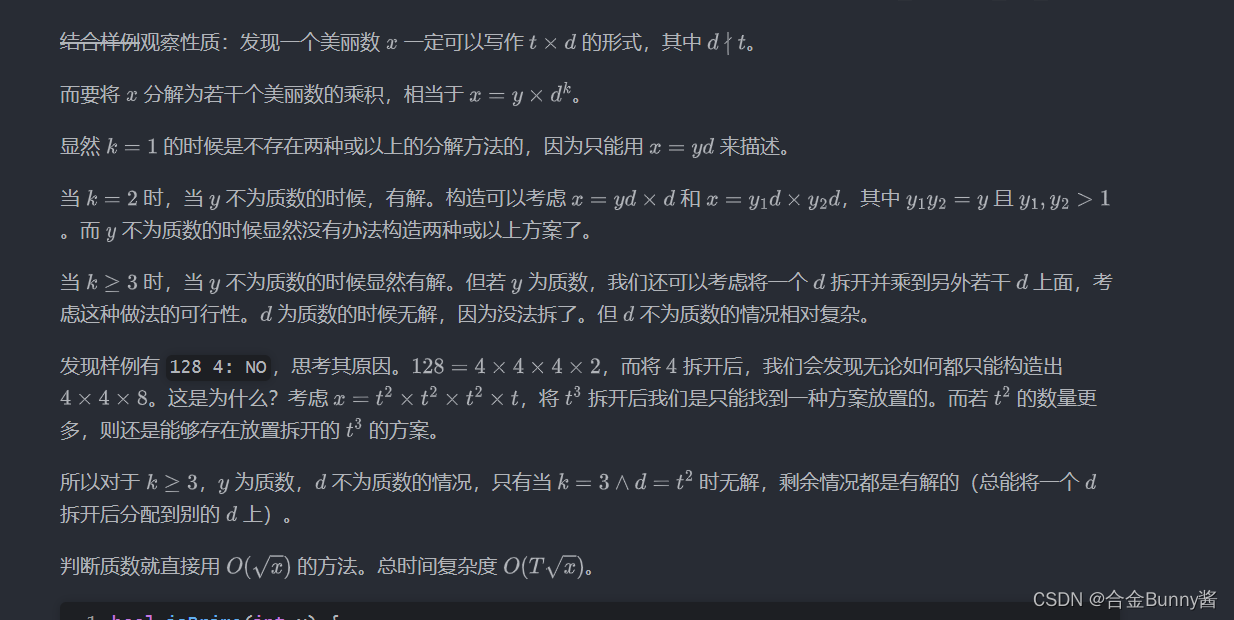
(图片来自别人写的题解,侵删。)
#include <bits/stdc++.h>
using namespace std;
// #define int long long
#define FOR(i, a, b) for (int i = (a); i <= (b); i++)
int T,x,d;
bool isprime(int x){
for(int i=2; i<=sqrt(x); i++)
if(x%i==0) return 0;
return 1;
}
inline void solve(){
int k=0;
while(x%d==0) x/=d, k++;
if(k==1) {cout<<"NO\n"; return;}
else if(k==2) {if(isprime(x)) cout<<"NO\n"; else cout<<"YES\n"; return;}
else if(k>=3 && isprime(x) && isprime(d)) {cout<<"NO\n"; return;}
else if(k==3 && isprime(x) && x*x==d) {cout<<"NO\n"; return;}
else cout<<"YES\n";
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin>>T; while(T--){
cin>>x>>d; solve();
}
}E. Madoka and the Sixth-graders?
思路参考了dls大佬的讲解,以及cf别人的代码。
【dls】【算法比赛】Codeforces Round #777 Div2 冲拳出击 轻松第一_哔哩哔哩_bilibili
?
//cf某位大佬写的,我只是写了注释给自己看
#include<bits/stdc++.h>
#define N 200100
using namespace std;
int n,p[30][N],us[N],out[N],d[N],g[N],TO[N];
set<int> a;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
int P;scanf("%d",&P);
p[0][i]=P; //记录所指位置
++d[P]; //记录每个位置的入度
}int A=0,mx=n;
for(int i=1;i<=n;++i)if(!d[i])++A; //入度为0的点的个数,也就是每次最大编号的增量
for(int i=1;i<=n;++i){
scanf("%d",g+i); //记录最终位置
mx=max(mx,g[i]); //取最大值,用于计算轮数
}
for(int j=1;j<30;++j)for(int i=1;i<=n;++i)p[j][i]=p[j-1][p[j-1][i]]; //连续记录30次倍增转移(一开始记了1次,这里再记29次)实际上是可以每次转移1,2,4,8.....1<<n次
int s=(mx-n)/A; //转移轮数
for(int i=1;i<=n;++i){ //遍历每个位置,模拟转移过程
int x=i,S=s; //x是当前位置,S是当前剩余要转移的次数
for(int j=29;j+1;--j) //[29~0]
if((1<<j)<=S)S-=1<<j,x=p[j][x]; //模拟转移
int v=g[x]; //i最终会转移到x位置,g[x]是这个位置最终的数字,说明:原本i上的数字>=g[x],并且有可能就是g[x](也就是v)
TO[i]=v; //out[i]>=v
if(!us[v])us[v]=1,out[i]=v; //由于i从1~n遍历,若!us[v]说明i就是最小到达v的编号,贪心地让i点原来的值就是v
}
for(int i=1;i<=n;++i)if(!us[i])a.insert(i); //空缺的位置,考虑放到set里面,等待分配
for(int i=1;i<=n;++i)if(!out[i]){ //遍历每个终点位置,如果是空的,就可以考虑放一个最小的数字
int v=*a.lower_bound(TO[i]); //贪心地把最小的数值分配给当前位置(当前位置就是目前可取的最小位置)
out[i]=v;a.erase(v); //记录结果,删除掉这个填过的位置
}
for(int i=1;i<=n;++i)printf("%d ",out[i]); //输出结果
}
?//本蒟蒻自己写的代码
#include <bits/stdc++.h>
using namespace std;
// #define int long long
#define FOR(i, a, b) for (int i = (a); i <= (b); i++)
const int N = 2e5+5;
int n, to[31][N], in[N], num[N], mx=0, cnt=0;
int mnVal[N], ans[N], vis[N];
set<int> st;
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin>>n; FOR(i,1,n) cin>>to[0][i], in[to[0][i]]++;
FOR(i,1,n) cin>>num[i], mx=max(mx,num[i]);
FOR(i,1,n) if(!in[i]) cnt++;
int sum=(mx-n)/cnt; //总的转移次数
FOR(i,1,30) FOR(j,1,n)
to[i][j] = to[i-1][to[i-1][j]]; //倍增转移
FOR(i,1,n){
int x=i, s=sum;
FOR(j,0,30)
if((1<<j)&s) s-=(1<<j), x=to[j][x];
mnVal[i] = num[x]; //记录i能取到的最小数字
if(!vis[num[x]]) ans[i] = num[x], vis[num[x]]=1; //如果该数字没用过,就分给i
}
FOR(i,1,n) if(!vis[i]) st.insert(i); //记录没用过的数字
FOR(i,1,n){
if(ans[i]) continue;
ans[i] = *st.lower_bound(mnVal[i]); //找到符合条件的最小的数字,填到i位置
st.erase(ans[i]); //st中删掉用过的数字
}
FOR(i,1,n) cout<<ans[i]<<' ';
}?