CSP 202112-3 登机牌条码
大模拟
做这类题首先一定要读懂题目,这种题往往不会有什么很高深的算法,就是对整个过程的一个模拟,一定要完全理解了题目的整个内容之后再开始写代码
题目整体可以分为两部分,第一部分是求数据码字,第二部分是求校验码,其中数据码字比较好求,看懂题目跟着题目走就可以了,求出数据码字就可以水40分了,后面的难点在于求校验码,这里我的代码只拿到了60分,但没有找到出错的地方,下面给大家详细写一下我的思路,希望能帮助到大家,如果大家找出了我代码中的错误,还请不吝赐教。
数据码字的求解
求数据码字就是给你一个字符串然后对其进行一个编码,其中各个字符所对应的值题目中都已经给出了,唯一需要注意的点就是三种模式的切换。
首先可以先写一个transmode函数用来进行三种模式的切换
void transmode(vector<int> &vec, int &oldm, int newm)
{
if (oldm == 1)
{
if (newm == 2)
vec.push_back(27);
if (newm == 3)
vec.push_back(28);
}
if (oldm == 2)
{
if (newm == 1)
{
vec.push_back(28);
vec.push_back(28);
}
if (newm == 3)
vec.push_back(28);
}
if (oldm == 3)
{
if (newm == 1)
vec.push_back(28);
if (newm == 2)
vec.push_back(27);
}
oldm = newm;
}
有了模式切换之后就可以对字符串进行一个初步的编码,定义一个mode变量用来保存当前的模式,遍历字符串,首先切换到当前字符的模式,然后加入字符的编码即可,最后注意是否需要填充字符,全部字符转换完成后,按照题目要求两两一组计算码字即可
vector<int> bianma(string s)
{
vector<int> ret;
int mode = 1; //当前模式:1:大写;2:小写;3:数字
for (char c : s)
{
if (isupper(c)) //大写字母
{
//将模式换为大写
if (mode != 1)
transmode(ret, mode, 1);
ret.push_back(c - 'A');
}
if (islower(c)) //小写字母
{
//将模式换为小写
if (mode != 2)
transmode(ret, mode, 2);
ret.push_back(c - 'a');
}
if (isdigit(c)) //数字
{
if (mode != 3)
transmode(ret, mode, 3);
ret.push_back(c - '0');
}
}
if (ret.size() % 2 != 0)
ret.push_back(29);
vector<int> mazi;
for (int i = 0; i < ret.size(); i += 2)
{
int temp = 30 * ret[i] + ret[i + 1];
mazi.push_back(temp);
}
return mazi;
}
得到码字之后,我们还需要计算数据码字,这里首先求出校验码字的个数(不需要求出),然后求出总数据所占的行数,并进一步求出填充字符的个数,以及数据码字的长度,与原码字组合得到最终的数据码字
vector<int> getsjmz(vector<int> mazi, int w, int s)
{
int jycnt = 0;
if (s != -1)
jycnt = pow(2, s + 1);
int cnt = 1 + mazi.size() + jycnt;
int line = ceil(double(cnt) / w);
int tccnt = w * line - cnt;
int len = w * line - jycnt;
vector<int> ret;
ret.push_back(len);
for (int i : mazi)
ret.push_back(i);
for (int i = 0; i < tccnt; i++)
ret.push_back(900);
return ret;
}
校验和的求解
求出数据码字后,我们就要开始校验和的求解了,这是本题的难点所在
首先我们先明确一个概念:通过向量来表示多项式,向量的下标是x的幂,对应的值为x的系数,例如向量{1,-2,3}所表达的多项式是:1-2x+3x2
明确了这个概念后我们就可以开始求解校验和了,我们将校验和的求解分成两部分,一是求解g(x)和d(x)多项式,二是进行多项式的取模运算求出r(x)
求解多项式
题目中给出:g(x)=(x-3)(x-32)…(x-3k)
我们先计算第一个(x-3)*(x-32)
这里我们首先通过乘法的分配律将其改写为(x-3)*x+(x-3)*(-32),
首先计算(x-3)*x,x-3对应的向量是{-3,1},(x-3)*x的结果为x2-3x,即{0,-3,1}。到这里大家应该看出规律了吧,一个多项式乘上xn,对应的结果就是向量向右移动n个位置,低位补0。
然后我们计算(x-3)*(-32),多项式运算的结果为-9x+27,对应的向量由{-3,1}变为{27,-9}即在原来的基础上乘上-9,由此我们又可以得出规律,一个多项式乘上一个系数,对应的结果就是向量的各位同时乘上这个系数
然后我们将这两个结果得到的向量相加最终得到{27,-12,1},对应的多项式为x2-12x+27,正是多项式运算的结果
下面通过一个手写版的可能更好看一些

//计算g(x)
vector<int> calcgx(int k)
{
vector<int> gx(k + 1, 0); // gx[i]表示x的i次方的系数
//初始值为x-3
gx[1] = 1;
gx[0] = -3;
//初始值依次乘(x-3^i)
for (int i = 2; i <= k; i++)
{
// temp保存原数组的值,将修改加到gx上
vector<int> temp;
temp.assign(gx.begin(), gx.end());
//整个数组向前推进一位
gx[0] = 0;
for (int j = 1; j <= k; j++)
gx[j] = temp[j - 1];
//整个数组都乘上-3^i,并将结果相加
for (int j = 0; j <= k; j++)
{
temp[j] *= -pow(3, i);
gx[j] += temp[j];
}
}
return gx;
}
//计算d(x)
vector<int> calcdx(vector<int> sjmz)
{
vector<int> ret;
for (int i = sjmz.size() - 1; i >= 0; i--)
ret.push_back(sjmz[i]);
return ret;
}
多项式取模
通过上面的方法,我们依次求出xkd(x)记为kd(x)以及g(x)后,就要计算kdx模gx的余数
这里我们以模拟竖式的方法来计算,通过下图我们可以将计算分为几个步骤
- 将除数乘上一个系数,使得被除数减除数之后能消掉最高位
- 被除数减除数
- 得到的结果继续按照第一步的方法计算,直到最终结果的最高位小于除数
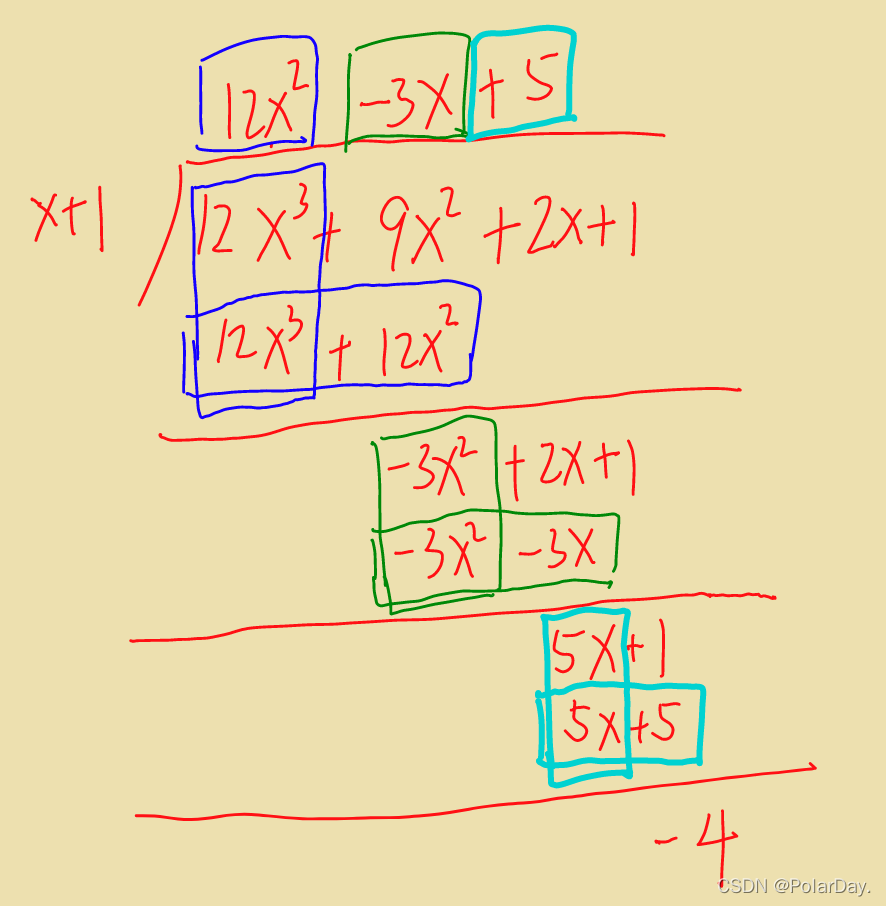
知道如何计算之后,我们将对多项式的运算换成对向量的运算就可以了,具体过程如下:

//计算校验码
vector<int> calcjx(int k, vector<int> sjmz)
{
// g(x)
vector<int> gx = calcgx(k);
// d(x)
vector<int> dx = calcdx(sjmz);
// x^k*d(x);整个数组向前推进x位
vector<int> kdx(dx.size() + k, 0);
for (int i = 0; i < dx.size(); i++)
kdx[i + k] = dx[i] % 929;
//计算kdx模gx的余数
int lenkdx = kdx.size();
int lengx = gx.size();
while (lenkdx >= lengx)
{
int xs = (kdx[lenkdx - 1] / gx[lengx - 1]) % 929;
int idx = 0;
for (int i = lenkdx - lengx; i < lenkdx; i++)
kdx[i] -= (gx[idx++] % 929 * xs % 929) % 929;
lenkdx--;
}
vector<int> ret;
ret.assign(sjmz.begin(), sjmz.end());
int i = lengx - 2;
//去掉头部的0
while (kdx[i] == 0)
i--;
for (; i >= 0; i--)
{
kdx[i] = (-kdx[i]) % 929;
if (kdx[i] < 0)
kdx[i] += 929;
ret.push_back(kdx[i]);
}
return ret;
}
至此这道题目的各种方法都已经实现完成了,下面放上题目的全部代码,再强调一下,这个代码只有60分,如果大家看完我的方法,发现有什么错误或是不妥的地方,还请不吝赐教。
#include <bits/stdc++.h>
using namespace std;
void transmode(vector<int> &vec, int &oldm, int newm)
{
if (oldm == 1)
{
if (newm == 2)
vec.push_back(27);
if (newm == 3)
vec.push_back(28);
}
if (oldm == 2)
{
if (newm == 1)
{
vec.push_back(28);
vec.push_back(28);
}
if (newm == 3)
vec.push_back(28);
}
if (oldm == 3)
{
if (newm == 1)
vec.push_back(28);
if (newm == 2)
vec.push_back(27);
}
oldm = newm;
}
vector<int> bianma(string s)
{
vector<int> ret;
int mode = 1; //当前模式:1:大写;2:小写;3:数字
for (char c : s)
{
if (isupper(c)) //大写字母
{
//将模式换为大写
if (mode != 1)
transmode(ret, mode, 1);
ret.push_back(c - 'A');
}
if (islower(c)) //小写字母
{
//将模式换为小写
if (mode != 2)
transmode(ret, mode, 2);
ret.push_back(c - 'a');
}
if (isdigit(c)) //数字
{
if (mode != 3)
transmode(ret, mode, 3);
ret.push_back(c - '0');
}
}
if (ret.size() % 2 != 0)
ret.push_back(29);
vector<int> mazi;
for (int i = 0; i < ret.size(); i += 2)
{
int temp = 30 * ret[i] + ret[i + 1];
mazi.push_back(temp);
}
return mazi;
}
vector<int> getsjmz(vector<int> mazi, int w, int s)
{
int jycnt = 0;
if (s != -1)
jycnt = pow(2, s + 1);
int cnt = 1 + mazi.size() + jycnt;
int line = ceil(double(cnt) / w);
int tccnt = w * line - cnt;
int len = w * line - jycnt;
vector<int> ret;
ret.push_back(len);
for (int i : mazi)
ret.push_back(i);
for (int i = 0; i < tccnt; i++)
ret.push_back(900);
return ret;
}
//计算g(x)
vector<int> calcgx(int k)
{
vector<int> gx(k + 1, 0); // gx[i]表示x的i次方的系数
//初始值为x-3
gx[1] = 1;
gx[0] = -3;
//初始值依次乘(x-3^i)
for (int i = 2; i <= k; i++)
{
// temp保存原数组的值,将修改加到gx上
vector<int> temp;
temp.assign(gx.begin(), gx.end());
//整个数组向前推进一位
gx[0] = 0;
for (int j = 1; j <= k; j++)
gx[j] = temp[j - 1];
//整个数组都乘上-3^i,并将结果相加
for (int j = 0; j <= k; j++)
{
temp[j] *= -pow(3, i);
gx[j] += temp[j];
}
}
return gx;
}
//计算d(x)
vector<int> calcdx(vector<int> sjmz)
{
vector<int> ret;
for (int i = sjmz.size() - 1; i >= 0; i--)
ret.push_back(sjmz[i]);
return ret;
}
//计算校验码
vector<int> calcjx(int k, vector<int> sjmz)
{
// g(x)
vector<int> gx = calcgx(k);
// d(x)
vector<int> dx = calcdx(sjmz);
// x^k*d(x);整个数组向前推进x位
vector<int> kdx(dx.size() + k, 0);
for (int i = 0; i < dx.size(); i++)
kdx[i + k] = dx[i] % 929;
//计算kdx模gx的余数
int lenkdx = kdx.size();
int lengx = gx.size();
while (lenkdx >= lengx)
{
int xs = (kdx[lenkdx - 1] / gx[lengx - 1]) % 929;
int idx = 0;
for (int i = lenkdx - lengx; i < lenkdx; i++)
kdx[i] -= (gx[idx++] % 929 * xs % 929) % 929;
lenkdx--;
}
vector<int> ret;
ret.assign(sjmz.begin(), sjmz.end());
int i = lengx - 2;
while (kdx[i] == 0)
i--;
for (; i >= 0; i--)
{
kdx[i] = (-kdx[i]) % 929;
if (kdx[i] < 0)
kdx[i] += 929;
ret.push_back(kdx[i]);
}
return ret;
}
int main()
{
int w, s;
string str;
cin >> w >> s >> str;
int k = pow(2, s + 1);
vector<int> mazi = bianma(str);
vector<int> sjmz = getsjmz(mazi, w, s);
//计算校验码
if (s != -1)
sjmz = calcjx(k, sjmz);
for (int i : sjmz)
cout << i << endl;
system("pause");
return 0;
}