[C++知识库]快速幂求A的B次方对C取余

题目如下：

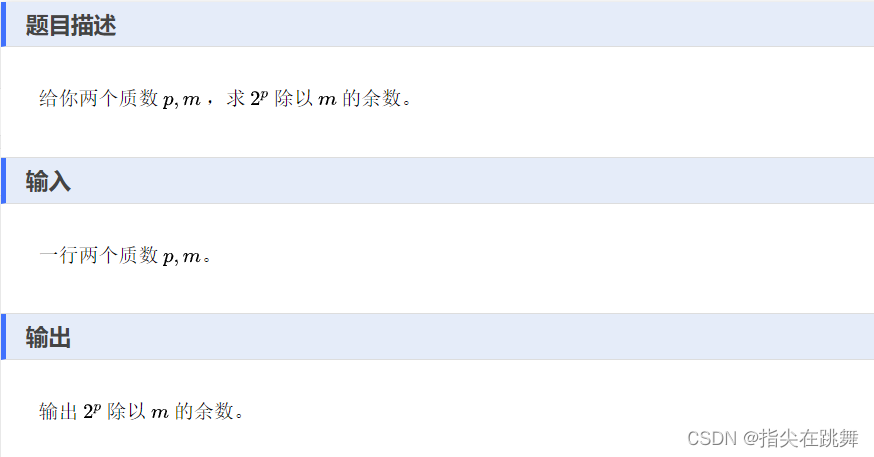
解法一：

最朴素的方法，直接循环b次，求出结果后对c取模

#include using namespace std;
int main() {
    int a,b,c,ans = 1;
    cin >> a >> b >> c;
    for(int i = 1;i <= b;i++) {
        ans *= a;
    }
    cout << (ans % c) << endl;
    return 0;
}

但是这么写有问题，如果b的值太大，会导致溢出和超时（指数爆炸），这里的复杂度是O(n)

解法二：快速幂

ab mod m 这个式子中，最容易导致超时的部分是ab，我们可以先思考一下这部分怎么算才快

假设，在草稿计算310，我们可以分解成310 = (32)5 = 95 = 9 * 94 = 9 * (81)2 = 9 * (811)2

可以发现一些规律：当指数为偶数的时候，将指数除以2，底数平方；当指数为奇数的时候，提取出一次方的底数，再将指数除以2，底数平方

这时候就可以设三个变量，设base为底数，设index为指数，设mod取模数，有了变量和规律，代码就不难了

另外，这里也要考虑数据范围问题，根据题目给出的范围，可能会造成指数爆炸，所以使用C++中long long来存储数据

这个的复杂度是O(log2n)

typedef long long ll;
#include using namespace std;
ll fast_pwoer(ll base,ll index,ll mod) {
    ll ans = 1;
    base %= mod;
    //指数为循环次数
    while (index) { 
    //判断奇偶性
        if (index % 2 == 1) {
            ans = (ans * base) % mod;
        }
        base = (base * base) % mod;
        index /= 2;
    }
    return ans;
}
int main() {
    int a,b,c;
    cin >> a >> b >> c;
    cout << (fast_pwoer(a,b,c)) << endl;
    return 0;
}

上边是别的大佬的思路，很厉害，放上原链接：

传送门

我的思路：
经过演草纸的推演，我发现先乘出结果再取模跟中间肆意取模的结果是一致的，那么我们就可以在中间每次乘法都进行一次取模运算，如此我们可以避免最后的数据过大超出数据类型所能表示的最大数值。
代码如下：

#include<iostream>
using namespace std;
typedef long long ll;

ll fun(ll base ,ll index, ll mod)
{
	ll ans =1;
	for(ll i=0;i<index;i++)
	{
		ans*=base;
		ans%=mod;
	}
	return ans;
}

int main()
{
	ll b,c;
	cin>>b>>c;
	cout<<fun(2,b,c)<<endl;
	return 0;	
}

感谢观看。