算法基础系列
前言
纯练习题,理论基础在上一篇博客,点击传送
算法基础–质数和约数
质数
模板题–试除法判定质数
传送门

一个个找
#include <iostream>
using namespace std;
const int N = 110;
int n, a[N];
bool is_prime(int x)
{
if (x < 2)
return false;
for (int i = 2; i <= x / i; i++)
if (x % i == 0)
return false;
return true;
}
int main()
{
cin >> n;
while (n--)
{
int x = 0;
scanf("%d", &x);
if (is_prime(x))
puts("Yes");
else
puts("No");
}
return 0;
}
模板题–分解质因数
#include <iostream>
using namespace std;
const int N = 110;
int n;
void divide(int x)
{
for (int i = 2; i <= x / i; i++)
{
if (x % i == 0)
{
int s = 0;
while (x % i == 0)
x /= i, s++;
cout << i << ' ' << s << endl;
}
}
if (x > 1)
cout << x << ' ' << 1 << endl;
puts("");
}
int main()
{
cin >> n;
while (n--)
{
int a;
cin >> a;
divide(a);
}
return 0;
}
模板题–筛质数
线性筛
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int prime[N], cnt;
bool st[N];
void get_prime(int x)//线性筛
{
for (int i = 2; i <= x; i++)
{
if (!st[i])
prime[cnt++] = i;
for (int j = 0; prime[j] <= x / i; j ++)
{
st[prime[j] * i] = true;
if(i % prime[j] == 0 )
break;//prime[j] 一定是i的最小质因子
}
}
}
int main()
{
int n;
scanf("%d", &n);
get_prime(n);
cout << cnt << endl;
return 0;
}
埃氏筛法
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int prime[N], cnt;
bool st[N];
void get_prime(int x)
{
for (int i = 2; i <= x; i++)
{
if (!st[i])
{
prime[cnt++] = x;
for (int j = i + i; j <= x; j += i)
st[j] = true;
}
}
}
int main()
{
int n;
scanf("%d", &n);
get_prime(n);
cout << cnt << endl;
return 0;
}
朴素筛法
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int prime[N],cnt;
bool st[N];
int n;
void get_prime(int x)
{
for (int i = 2; i <= x; i++)
{
if(!st[i])
prime[cnt++] = x;
for (int j = i + i; j <= x; j += i)
st[j] = true;
}
}
int main()
{
scanf("%d", &n);
get_prime(n);
cout << cnt << endl;
return 0;
}
X的因子链
传送门

多重集合的排列数问题
线性筛法
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = (1 << 20) + 10; // 1的20 次方+10
int prime[N], min_p[N], cnt;
bool st[N];
void get_prime(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i])
{
min_p[i] = i;
prime[cnt++] = i;
}
for (int j = 0; prime[j] * i <= n; j++)
{
int t = prime[j] * i;
st[t] = true;
min_p[t] = prime[j];
if (i % prime[j] == 0)
break;
}
}
}
int main()
{
get_prime(N - 1);
int fact[30], sum[N];
int x;
while(~scanf("%d",&x))
{
int k = 0, tot = 0;
while(x > 1)
{
int p = min_p[x];
fact[k] = p, sum[k] = 0;
while(x %p == 0)
{
x /= p;
sum[k]++;
tot++;
}
k++;
}
LL res = 1;
for (int i = 1; i <= tot; i ++)
res *= i;//求阶乘
for (int i = 0; i < k; i++)
for (int j = 1; j <= sum[i]; j ++)
res /= j;
printf("%d %lld\n", tot, res);
}
return 0;
}
约数
模板题–试除法求约数
传送门
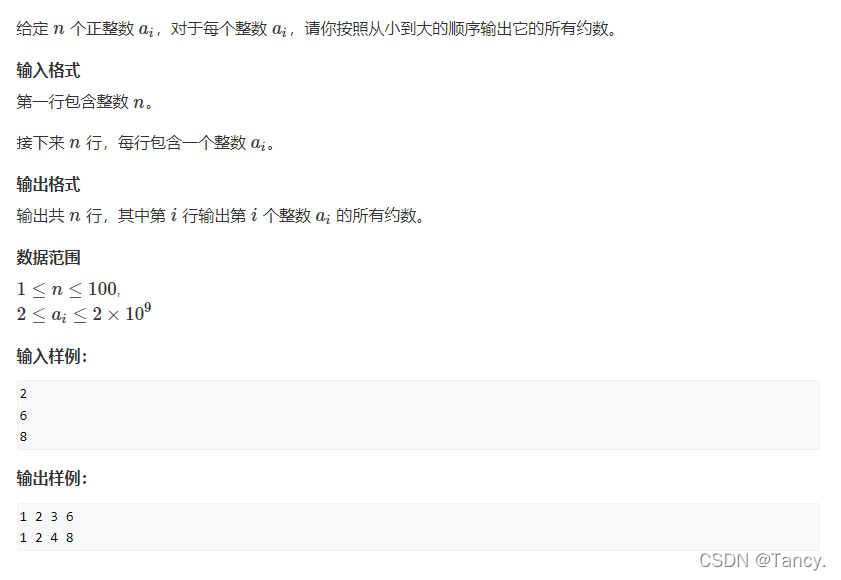
模板题
精髓在于,用了vector动态数组和auto
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
vector<int> get_divesors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i++)
if (x % i == 0) //合数有两个
{
res.push_back(i);
if (i != x / i) //避免放重复
res.push_back(x / i);
}
sort(res.begin(), res.end()); //因为是一大一小放入,乱序的
return res;
}
int main()
{
int n;
cin >> n;
while (n--)
{
int x;
cin >> x;
auto res = get_divesors(x);
for (auto x : res)
cout << x << ' ';
cout << endl;
}
return 0;
}
模板题–约数个数
传送门
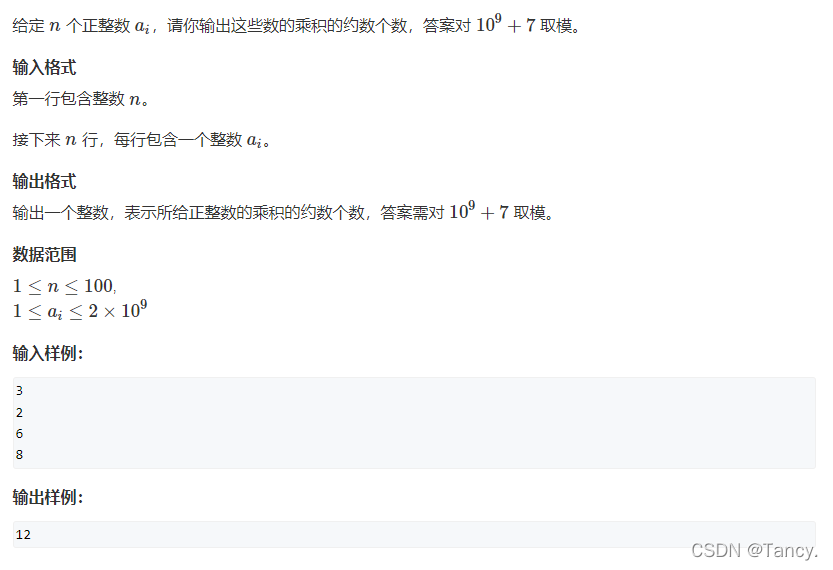
这题就是一个公式,记住即可
精髓:map + auto 太妙了
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n--)
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i++)
while (x % i == 0)
{
x /= i;
primes[i]++;
}
if (x > 1)
primes[x]++;
}
LL res = 1;
for (auto prime : primes)
res = res * (prime.second + 1) % mod;
cout << res << endl;
return 0;
}
模板题–约数之和
传送门

同上一个题,是一个公式,具体可在前言部分跳转查看
精髓:map + auto 太妙了
这两个题的主题部分都一样,要求出底数和指数,区别在于结果的处理方法
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n--)
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i++)
while (x % i == 0)
{
x /= i;
primes[i]++;
}
if (x > 1)
primes[x]++;
}
LL res = 1;
for (auto prime : primes)
{
LL p = prime.first, d = prime.second;
LL t = 1;
while(d--)
t = (t * p + 1) % mod;
res = res * t % mod;
}
cout << res << endl;
return 0;
}
模板题–最大公约数
纯纯模板题,标准的gcd模板
有内置函数
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int gcd(int a, int b)
{
return b ? gcd(b,a % b) : a;
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", gcd(a, b));
}
return 0;
}
等差数列
传送门

思路:
每一项与第一项的差一定是d的倍数
当d != 0 时, (a末 - a初) / d + 1 ---- 让公差d最大即可
当d == 0 时,答案为 n
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
int a[N];
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
sort(a, a + n);
int d = 0;
for (int i = 1; i < n; i++)
d = gcd(d, a[i] - a[0]);
if (d == 0)
printf("%d", n);
else
printf("%d", (a[n - 1] - a[0]) / d + 1);
return 0;
}


