前言
这几天在学习计算机网络,里面稍微讲到了加密,受到之前加密货币浪潮的影响,一直想看看非对称加密是怎么来的,就挑了一个背包加密问题来看看,确实不错,这里分享一下要点、例子和自己编的c++程序。
非对称加密入门
为对称加密是加密和解密不相同,理解为加密用锁,解密用钥匙,那个锁就是公钥,一般可以公开,而那个钥匙是私钥,只有被授权的解密者才可以拥有。除了私钥外,还有两个量:m和n也是背包问题的解密者需要知道的。
加密前的加明文,加密后的叫密文。
超递增序列
所谓的“超递增序列”是我们马上要使用的一个概念,普通的递增序列是后一个数比第一个大的序列,如:1 2 3 4 ,但超递增序列是后一个数要比前面所有的数还要大的序列,如1 2 5 15 100.下面的例子我们不妨就用这个序列来。
背包密码的概念
这是一个背包问题衍生而来的加密/解密算法,所以起了一个草率的名字——背包密码问题。所谓的背包问题就是包里面装了多少东西和包的总重量是知道的,而每样东西多重是不知道的。
私钥和公钥的构建
私钥的要求就是一个超递增序列,上面说好了,就用1 2 5 15 100,公钥在构造时,先创建两个数:m和n,其中m是一个大于私钥序列中所有数字之和的数,私钥序列之和是1+2+5+15+100=123,不妨设m=200。再设一个n,n和m要求互质,即两者不能有公共的质数,那选一个质数3,3又不是200的质数,所以3符合,令n=3。至此,私钥和m,n都已经草率地定下来了。
公钥怎么计算呢?需要把私钥的每一个数字都乘上n,再除以m,余数就是公钥的数字了。比如(13)mod200=3,(23)mod200=6,依次往下,得到公钥序列为:3 6 15 45 100,我们把现在已经构建好的数罗列一下:
| 私钥 | 1 | 2 | 5 | 15 | 100 |
|---|---|---|---|---|---|
| 公钥 | 3 | 6 | 15 | 45 | 100 |
| m | 200 | ||||
| n | 3 |
加密
这里使用公钥进行加密,明文选21吧,换算成二进制,10101B,用10101和3 6 15 45 100进行类似“与”的操作,把明文里面1对应的序列加起来,也就是3+15+100=118.这个118就是密文了。
解密
解密者拥有的东西就在上面的表里面,其实严格来说公钥在解密时是可以不需要的,但既然都是公开的了,也可以算是知道的,都无所谓了,反正用不到。。。。
通过n和m先构建一个数,叫“n的逆模”,我们令其为n’,n、n‘、m三者的关系是:
- (nn’) mod m = 1
所以取一个n’,为67,满足上式条件。再把密文乘n’,其积与m做mod,在这里即为:(11867) mod 200 = 106,即获得了106,这个106是什么呢?可以理解为上面密文的118是明文与公钥“与”的结果,而这个106是明文与私钥“与”的结果。
把106带入到私钥序列里面,反解明文,因为私钥是超递增的,所以解唯一,是10101,答案正确。
以上就是背包密码的加密与解密过程。
c++实现
给一个自己写的一个非常简单的c++程序,计算逻辑完全按照上面的文字来的,输入明文可以输出密文,并反解明文。
Ver_1版本的界面如图,没有弄进制转换,输入私钥和明文需要使用二进制,红色框子那里可以随便更改。
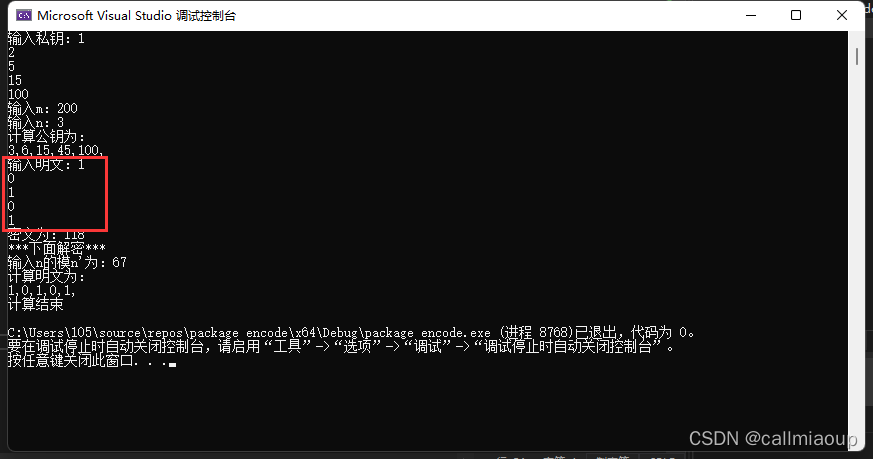
Ver_2版的可以直接输入明文的十进制,私钥的输入也不是逐个输入,而是所有序列一起输入,最后回车导入内存。
两个版本的代码都在github,链接如下:https://github.com/evandworld/Knapsack
如果有建议欢迎交流