[C++知识库]2017蓝桥杯C/C++B组国赛-瓷砖样式

题目

题目链接

题解

DFS。

方案需要满足的要求：

1. 只能有黄和橙两种颜色；
2. 必须填满；
3. 任何一种颜色都不允许同时出现在 $2\times 2$ 的方格中；
4. 任意一种颜色图案都必须能由 $2\times 1$ 或 $1\times 2$ 的长方形瓷砖拼成；
5. 瓷砖不能切割，不能重叠，也不能只铺一部分；
6. 只考虑组合图案，忽略瓷砖的拼缝.

举几个反例：

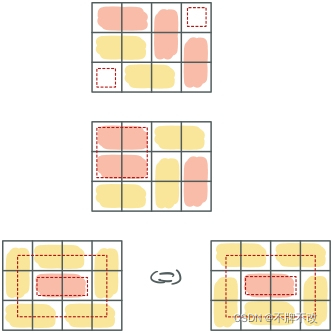
最后一种容易忽略。

想过二进制枚举，但是二进制枚举的话，对于枚举到的每种状态不好判断是否满足要求。所以还是得用DFS。

由于要求两种颜色的图案都要能用 $2\times 1$ 或 $1\times 2$ 的瓷砖拼成，所以遍历到某个格子时要分别尝试着贴黄色瓷砖和橙色瓷砖。

（如果要是只dfs一种颜色的瓷砖，另一种颜色的瓷砖贴在剩下的地方，那么这无法保证剩下的位置一定能由 $2\times 1$ 或 $1\times 2$ 的瓷砖拼成。你说你想在找到方案时判断一下另一种颜色的图案是否可行，这不又回归到为什么二进制枚举不好实现了嘛）

如果遍历到的这个格子已经贴上了瓷砖，那么就不能再贴瓷砖了，继续判断下一个位置；如果遍历到的格子没贴上瓷砖，则必须在这个位置贴上瓷砖（“必须填满”），可以选择黄色或橙色。对于要贴瓷砖的情况，可以选择向上下贴，也可以选择左右贴。

我们按照从上往下，从左到右的顺序DFS，即先看第一行的每一列，再看第二行的每一列。当到达每一列的倒数第二块瓷砖时，我们就要将DFS的参数调整为下一行的第一个瓷砖了。

对于上图中的第三种不合法情况，我们没有什么好的技巧，只能通过 $map$ 存起来，每次判断完 $2\times 2$ 的方格中是否并非全色，之后再去判断该方案是否已经保存过，没保存过说明这是新方案，统计一下。

对于方案的保存，我们可以使用二进制的方式，因为总共两种颜色。

代码

#include<bits/stdc++.h>
using namespace std;

const int N = 3, M = 10;

int vis[N+1][M+1], ans;
unordered_map<int, int> hash_;

bool check () {
	for (int i = 1;i < N;i ++)
	for (int j = 1;j < M;j ++)
	if ((vis[i][j] && vis[i+1][j] && vis[i][j+1] && vis[i+1][j+1]) || 
		(!vis[i][j] && !vis[i+1][j] && !vis[i][j+1] && !vis[i+1][j+1]))
		return false;
	return true;
}

void dfs (int x, int y) {
	if (x > N) {
		if (check ()) {
			int res = 0;
			for (int i = 1;i <= N;i ++)
			for (int j = 1;j <= M;j ++)
			res = (res << 1) + vis[i][j];
			
			if (!hash_[res])
				hash_[res] = 1,
				ans ++;
		}
		return ;
	}
	
	int tx, ty;
	if (y + 1 > M) ty = 1, tx = x + 1;
	else ty = y + 1, tx = x;
	
	if (vis[x][y]==-1) {
		if (x < N && vis[x+1][y]==-1) {
			vis[x][y] = vis[x+1][y] = 0;
			dfs (tx, ty);
			vis[x][y] = vis[x+1][y] = 1;
			dfs (tx, ty);
			vis[x][y] = vis[x+1][y] = -1;
		} 
		
		if (y < M && vis[x][y+1]==-1) {
			vis[x][y] = vis[x][y+1] = 0;
			dfs (tx, ty);
			vis[x][y] = vis[x][y+1] = 1;
			dfs (tx, ty);
			vis[x][y] = vis[x][y+1] = -1;
		}
	} else {
		dfs (tx, ty);
	}
}

int main()
{
	memset (vis, -1, sizeof vis);
	dfs (1, 1);
	cout << ans << endl;
	return 0;
}