题干
Egor has a table of size n×m, with lines numbered from 1 to n and columns numbered from 1 to m. Each cell has a color that can be presented as an integer from 1 to 105.
Let us denote the cell that lies in the intersection of the r-th row and the c-th column as (r,c). We define the manhattan distance between two cells (r1,c1) and (r2,c2) as the length of a shortest path between them where each consecutive cells in the path must have a common side. The path can go through cells of any color. For example, in the table 3×4 the manhattan distance between (1,2) and (3,3) is 3, one of the shortest paths is the following: (1,2)→(2,2)→(2,3)→(3,3).
Egor decided to calculate the sum of manhattan distances between each pair of cells of the same color. Help him to calculate this sum.
Input
The first line contains two integers n and m (1≤n≤m, n?m≤100000) — number of rows and columns in the table.
Each of next n lines describes a row of the table. The i-th line contains m integers ci1,ci2,…,cim (1≤cij≤100000) — colors of cells in the i-th row.
Output
Print one integer — the the sum of manhattan distances between each pair of cells of the same color.
Examples
inputCopy
2 3
1 2 3
3 2 1
outputCopy
7
inputCopy
3 4
1 1 2 2
2 1 1 2
2 2 1 1
outputCopy
76
inputCopy
4 4
1 1 2 3
2 1 1 2
3 1 2 1
1 1 2 1
outputCopy
129
Note
In the first sample there are three pairs of cells of same color: in cells (1,1) and (2,3), in cells (1,2) and (2,2), in cells (1,3) and (2,1). The manhattan distances between them are 3, 1 and 3, the sum is 7.
题意
给矩阵中每个单元格涂上颜色,求出所有相同颜色的单元格距离之和。
距离 == abs(x1-x2) + abs(y1-y2)
思路
用vector存储颜色相同的坐标,方便遍历。
我尝试找到答案与整体坐标的关系,太菜了,最后还是看的别人推出的公式。
两个相同颜色单元格的距离 即 横坐标之差 加 纵坐标之差,那么在颜色相同的单元格中:
任意两个单元格的距离之和 = 任意两个单元格的横坐标差之和 + 这两个单元格的纵坐标差之和。
我们可以分开计算横、纵坐标差之和。
横坐标差之和:
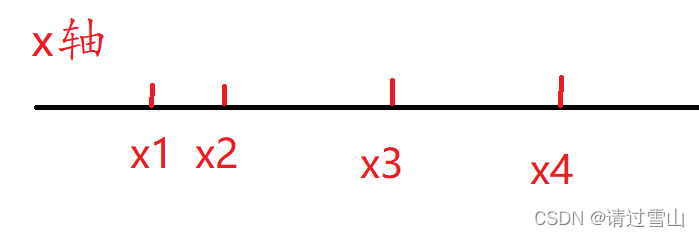
将横坐标升序排列,遍历所有坐标,第 i 个坐标与前面所有坐标差之和为
xi * (i-1) - (x1+x2+x3+… …+xi-1);
例如 i == 1时,第1个坐标与前面所有坐标差之和为:x1 * 0 - 0
i == 2时为:x2 * 1 - (x1)
i == 3时为:x3 * 2 - (x1 + x2)
i == 4时为:x4 * 3 - (x1 + x2 + x3)
…
上述各式之和即为 任意两个相同颜色单元格横坐标之和。
纵坐标同理。
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <vector>
#include <cstring>
#include <string>
#include <string.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10, M = 1e6+10;
typedef struct node{
int x,y;
};
bool cmp1(node a, node b){
return a.x < b.x;
}
bool cmp2(node a, node b){
return a.y<b.y;
}
vector<node> v[N];
int a[1010][1010];
int main(){
int n,m,r=0;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++){
int a;
scanf("%d",&a);
if(a>r)//r 为颜色种类数
r=a;
v[a].push_back({i, j});
}
ll ans=0;
for(int i=1;i<=r;i++){
ll s=0;
sort(v[i].begin(), v[i].end(), cmp1);//横坐标
for(ll j=0;j<v[i].size();j++){
ans+= j * v[i][j].x - s;
s+=v[i][j].x;
}
s=0;
sort(v[i].begin(), v[i].end(), cmp2);//纵坐标
for(ll j=0;j<v[i].size();j++){
ans+= j * v[i][j].y - s;
s+=v[i][j].y;
}
}
printf("%lld",ans);
return 0;
}