[C++知识库]中缀表达式求值

根据输入的中缀表达式构造一棵等价的中缀表达式树，并通过此树计算中缀表达式的值。

通过中缀表达式树计算中缀表达式：

一、构造中缀表达式树：

①初始化操作数栈和运算符栈；

②扫描中缀表达式：

• 若扫描到操作数，压入操作数栈；
• 若扫描到界限符，遇到(直接压入运算符栈，遇到)依次弹出运算符栈内运算符，直到弹出(；
• 若扫描到运算符，依次弹出运算符栈中优先级高于或等于当前运算符的所有运算符，直到遇到(或运算符栈空，之后再将当前运算符压入运算符栈；
• 若扫描到等于号，依次弹出运算符栈中的所有运算符。
• 同时：a.每次压栈时，将操作数或运算符转化为二叉树结点形式再压栈。b.每当运算符栈中弹出运算符时，依次弹出操作数栈中的两个元素作为右操作数和左操作数，分别挂在当前运算符结点的左右孩子处，之后将当前子树作为一个操作数压入操作数栈。

二、通过后序遍历递归计算中缀表达式树。

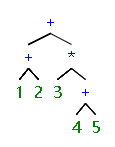
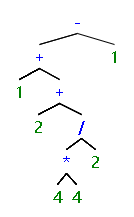
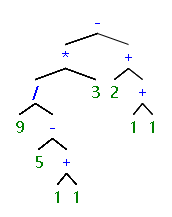
输入样例：
1+2+3*(4+5)=
1+(2+4*4/2)-1=
((9/(5-(1+1)))*3)-(2+(1+1))=
=

输出样例：
30
10
5

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MaxSize 10
#define ElemType BiTree

typedef struct BiTNode {
    char data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

typedef struct SqStack {
    ElemType data[MaxSize];
    int top;
} SqStack;

BiTree BiTreeCreate(char *nodeData);
void BiTreeDestroy(BiTree *root);
BiTNode *nodeCreate(char c);

int calculate(BiTree root);
bool isLessOrEqual(char c1, char c2);

/*为简化代码，所有的栈操作都不作出错检查*/
void StackInit(SqStack *stack);
bool StackEmpty(SqStack stack);
void StackPush(SqStack *stack, ElemType e);
ElemType StackPop(SqStack *stack);
ElemType StackGetTop(SqStack stack);

int main() {
    char str[MaxSize] = "";

    while (scanf("%[^\n]%*c", str) && str[0] != '=') {
        BiTree T = NULL;

        T = BiTreeCreate(str);
        printf("%d\n", calculate(T));

        BiTreeDestroy(&T);
    }
    return 0;
}

/**
 * 根据中序表达式构造二叉表达式树
 */
BiTree BiTreeCreate(char *nodeData) {
    SqStack numStack;//操作数栈
    SqStack opStack;//运算符栈
    BiTNode *op;//用于暂存出栈的运算符

    StackInit(&numStack);
    StackInit(&opStack);

    for (int i = 0; nodeData[i] != 0; i++) {
        if (nodeData[i] >= 48 && nodeData[i] <= 57) {
            /*当前结点是操作数，直接压操作数栈*/
            StackPush(&numStack, nodeCreate(nodeData[i]));
        } else if (nodeData[i] == '+' || nodeData[i] == '-' || nodeData[i] == '*' || nodeData[i] == '/') {
            if (!StackEmpty(opStack)) {
                op = StackGetTop(opStack);
                if (isLessOrEqual(nodeData[i], op->data)) {
                    /*当前运算符优先级低于或等于栈顶运算符，将栈顶运算符出栈并运算*/
                    op = StackPop(&opStack);
                    /*将左、右操作数挂在左、右孩子位置上的过程就相当于运算*/
                    op->rchild = StackPop(&numStack);
                    op->lchild = StackPop(&numStack);
                    /*运算结果相当于一个操作数*/
                    StackPush(&numStack, op);
                }
            }
            StackPush(&opStack, nodeCreate(nodeData[i]));
        } else if (nodeData[i] == '(') {
            /*左括号直接压栈*/
            StackPush(&opStack, nodeCreate(nodeData[i]));
        } else if (nodeData[i] == ')') {
            /*如果遇到右括号，运算符栈一直出栈并运算，直到左括号出栈*/
            while (1) {
                op = StackPop(&opStack);
                if (op->data != '(') {
                    op->rchild = StackPop(&numStack);
                    op->lchild = StackPop(&numStack);
                    StackPush(&numStack, op);
                } else {
                    break;
                }
            }
        } else {
            /*遇到等号将栈中剩余运算符出栈运算，并将结果返回*/
            while (!StackEmpty(opStack)) {
                op = StackPop(&opStack);
                op->rchild = StackPop(&numStack);
                op->lchild = StackPop(&numStack);
                StackPush(&numStack, op);
            }
            return op;
        }
    }
}

/**
 * 释放二叉树内存空间
 */
void BiTreeDestroy(BiTree *root) {
    if (*root) {
        BiTreeDestroy(&(*root)->lchild);
        BiTreeDestroy(&(*root)->rchild);
        free(*root);
        *root = NULL;
    }
}

/**
 * 将输入数据转化为二叉树结点
 */
BiTNode *nodeCreate(char c) {
    BiTNode *newNode = (BiTNode *) malloc(sizeof(BiTNode));

    newNode->data = c;
    newNode->lchild = newNode->rchild = NULL;
    return newNode;
}

/**
 * 通过表达式树进行计算
 */
int calculate(BiTree root) {
    if (root) {
        switch (root->data) {
            case '+':
                return calculate(root->lchild) + calculate(root->rchild);
            case '-':
                return calculate(root->lchild) - calculate(root->rchild);
            case '*':
                return calculate(root->lchild) * calculate(root->rchild);
            case '/':
                return calculate(root->lchild) / calculate(root->rchild);
            default:
                return root->data - 48;
        }
    }
}

/**
 * 判断c1的优先级是否小于c2
 */
bool isLessOrEqual(char c1, char c2) {
    int priority1 = 1, priority2 = 1;

    if (c1 == '(') {
        priority1 = 0;
    } else if (c1 == '*' || c1 == '/') {
        priority1 = 2;
    }

    if (c2 == '(') {
        priority2 = 0;
    } else if (c2 == '*' || c2 == '/') {
        priority2 = 2;
    }

    return priority1 <= priority2;
}

/**
 * 初始化栈
 */
void StackInit(SqStack *stack) {
    stack->top = -1;
}

/**
 * 判栈空
 */
bool StackEmpty(SqStack stack) {
    return (stack.top == -1) ? true : false;
}

/**
 * 入栈
 */
void StackPush(SqStack *stack, ElemType e) {
    stack->data[++stack->top] = e;
}

/**
 * 出栈
 */
ElemType StackPop(SqStack *stack) {
    return stack->data[stack->top--];
}

/**
 * 取栈顶元素但不出栈
 */
ElemType StackGetTop(SqStack stack) {
    return stack.data[stack.top];
}