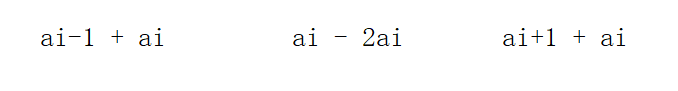灵能传输
题目思路:
这道题是一道贪心题,需要一定的数学证明, 同时我们还需要结合前缀和,寻找规律,从而找出最优解。
分析:
题目要求:
- 对于灵能ai > 0的武士,会分别给ai - 1和ai + 1传输ai的灵能值
- 对于灵能ai < 0的武士,需要ai - 1和ai + 1各传输ai的灵能值给它
我们分别对这两种情况进行分析:
- ai > 0:
- ai < 0:
我们可以发现,其实两种操作的结果都是一样的。
这时我们在导入前缀和进行分析:
这是我们可以发现:对ai进行操作等价于对si-1和si进行交换。
好!现在问题又来了,这对解题有什么用呢,其实这还只是一个过度,后面还要继续分析证明!!!
题目要我们求MAX(i:1-n)| ai |的最小值,而ai = si - si-1,所以我们可以发现,如果要使的最小的最大|ai|,那么我们要尽可能的让曲线s变得单调。
例如:
这是我们可能会想到,对其进行排序,因为对于ai的操作就相当于对si和si-1进行交换,这就和冒泡排序一样了,且任何乱序都能排成有序,有序也可以排成任何乱序。
但现在问题又出现了!!!
题目规定了不能对a1和an进行操作,也就是说s0和s1是不能交换的,sn-1和sn是不能交换的,这时我们又要进行分析了。
既然s0和sn这两个数时不能交换的,所以我们在保证符合条件的情况下尽可能的对其排序,十七更具有单调性。
首先我们假设一种情况:s0 < sn
我们从y轴看这个图,把这些线段想象成点,毕竟实际上就是点,从y轴看我们会发现,②比①的点更加稠密,并且因为s0<sn,所以s0到max的波动比sn到max更大,同理min也是如此。
而当s0 > sn时,这种情况其实我们不需要考虑,当s0 > sn时,我们就将曲线反过来看,从sn开始,s0结束,此时又是一个左端点小于右端点的情况了,然后我们用s0表示之前的sn,此时就与上面的情况一样了。
那么现在我们就知道要做什么了,其实就是尽可能的让最小值靠近s0,最大值靠近sn,但我们又该如何进行操作呢?
如图分析:
如何走才能使得max(si - si-1)最小呢?这时候我们就该考虑s0该如何走了。
对于sn这边也是一样的。
代码如下:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 300010;
int n, T;
LL a[N], s[N]; //分别记录值和前缀和
bool st[N]; //用于标记
int main(){
scanf("%d", &T);
while(T--){
s[0] = 0;//由于会有多次测试,所以我们要对s[0]进行初始化
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]), s[i] = s[i - 1] + a[i];
//记录s0和sn的值
LL s0 = s[0], sn = s[n];
//如果大于我们就交换一下
if(s0 > sn)swap(s0, sn);
//排序
sort(s, s + 1 + n);
//找到排序后,也就是y轴上看的情况,s0和sn的下标
for(int i = 0; i <= n; i++)
if(s0 == s[i]){
s0 = i;
break;
}
for(int i = n; i >= 0; i--)
if(sn == s[i]){
sn = i;
break;
}
memset(st, false, sizeof st);
//从s0到min,开始,从左隔个往a里赋值
int l = 0, r = n;
for(int i = s0; i >= 0; i -= 2){
a[l++] = s[i];
st[i] = true;
}
//与s0操作一样,但是是往右走
for(int i = sn; i <= n; i += 2){
a[r--] = s[i];
st[i] = true;
}
//最后将剩余点补满
for(int i = 0; i <= n; i++)
if(!st[i]){
a[l++] = s[i];
st[i] = true;
}
LL res = 0;
//找到最大的s[i]-s[i-1];
for(int i = 1; i <= n; i++)res = max(res, abs(a[i] - a[i - 1]));
printf("%lld\n", res);
}
return 0;
}