数据类型
整型:char short int long longlong
浮点型:float double …
构造类型:数组 结构体 枚举 联合体…
指针类型:char* int* …
整型在内存中的存储
我们都知道,数据在内存中以二进制的形式存储。
对于整数而言,二进制的表示方式有三种:原码,反码,补码(以补码形式存于内存)
正整数:原反补相同
负整数:直接写出是原码,原码符号位不变其他取反为反码,反码加1为补码
举个例子:
十进制:-15
二进制原码:1000000000000000000000000001111
反码: 11111111111111111111111111110000
补码: 1111 1111 1111 1111 1111 1111 1111 0001
补码十六进制:ff ff ff f1
验证: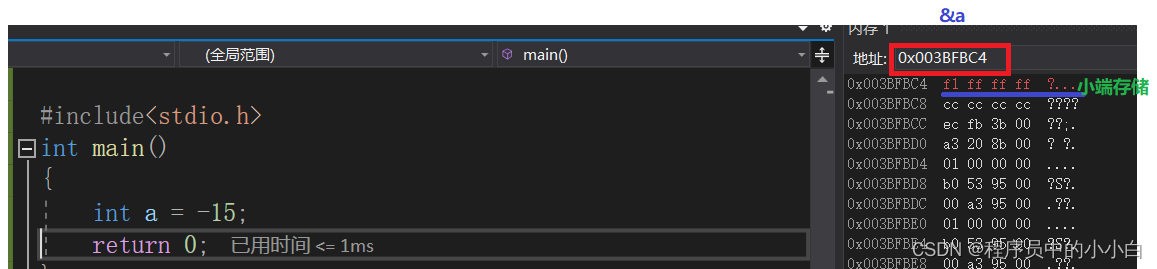
整数在内存中既然真的以补码形式存储,那为什么这样做呢?
我们通常用整数进行计算,而我们知道计算机的CPU负责这个任务,但是CPU上只有加法器,倘若我们想计算
-1+1
原码:10000000000000000000000000000001
+00000000000000000000000000000001
结果:10000000000000000000000000000010
结果本应该是0,可是这么看来加起来会变成-2,显然是算错了,可是计算机会出现这种错误吗?
我们在用补码进行一次运算
11111111111111111111111111111111
+ 00000000000000000000000000000001
=100000000000000000000000000000000(最前面的1溢出丢弃,结果为零)
这样看来就可以将符号位与数值位进行统一计算
除此以外原码到补码的转换是可逆的,可以逆回去运算也可以用相同的方法算回去。
大小端问题
通过上面的验证,我们不难发现整数在内存中存储数据是倒序的。也就是小端存储。
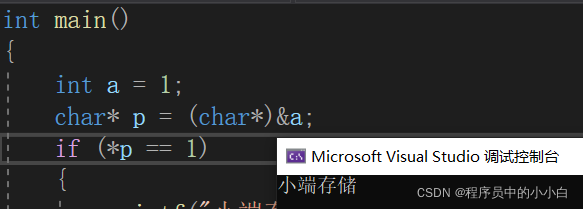
大端字节序:把数据的低位字节序的内容存放在高地址处,高位字节序的内容存放在低地址处
小端字节序:把数据的高位字节序的内容存放在高地址处,低位字节序的内容存放在低地址处
char类型变量在内存中的存储
char:00000000~11111111
signed char:-128~127(最高位为符号位)
unsigned char:0~255
浮点型在内存中的存储
存储
IEEE 754标准规定
浮点数的表示形式:(-1)sM2E
s:0 / 1
1<=M<2
E:指数
例如:5.5
十进制:5.5
二进制:101.1
科学表示:(-1)01.01122(s=0,M=1.011,E=2)
那内存中是如何存储这些数据呢?

s:存放0(正数)或者1(负数),表示符号位
M(1<=M<2):1.xxxxxxxx,因此不需要存储1,只需要存储小数点后的数字,提高精度
E:为无符号数,存放正数,但是E可以存放负数,只需要加上一个中间值
内存存放的E=原本的E+127(8bit)/+1023(11bit)
读取
s与M直接按照存储方式读出来
指数E从内存中取出分为三种情况:
1、E不为全0或者不为全1
E=内存中的E-127(8bit)/ -1023(11bit)
2、E为全0
E=1-127/1-1023,说明原来的E非常小,整个数接近于0,符号取决于s
3、E为全1
原来的E非常大,整个数趋近于无穷大,符号取决于s