题目描述
棋盘上 AA 点有一个超级过河卒,需要走到目标 BB 点。卒行走的规则:可以向上下左右走。同时在棋盘上 CC 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,AA 点 (0, 0)(0,0)、BB 点 (n, m)(n,m),同样马的位置坐标是需要给出的。
现在要求你计算出卒从 AA 点能够到达 BB 点的任意一条最短路径,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 BB 点坐标和马的坐标。
输入输出样例
输入
6 6 3 3
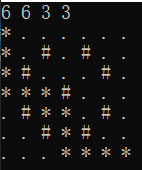
输出
(#代表马的可控范围,*代表路线)
题解
这道题用到了bfs和递归的思想,bfs部分不再赘述。
这道题我用了nxt数组来存该点的上一个坐标,也就是从哪一个点可以到这里,最后更新的值一定是最优的,然后从print(next[x1][y1][0],next[x1][y1][1])向前递归即可
#include <iostream>
#include <queue>
using namespace std;
int x1, yy1;//终点坐标
int x2, y2;//马的坐标
char map[25][25];
int hf[8][2] = { {-2, -1}, {-1, -2}, {1, -2}, {2, -1}, {2, 1}, {1, 2}, {-1, 2}, {-2, 1} };//马可以走的8个方向
int f[4][2] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
int nxt[25][25][2];//我的下一个坐标
struct node {
int x, y;//当前点坐标
};
void print(int x, int y)
{
if (x == -1 && y == -1)
{
return;
}
else
{
print(nxt[x][y][0], nxt[x][y][1]);
//cout << nxt[x][y][0] << "," << nxt[x][y][1] << endl;
map[nxt[x][y][0]][nxt[x][y][1]] = '*';
}
}
void map_print()
{
for (int i = 0; i <= x1; i++)
{
for (int j = 0; j <= yy1; j++)
{
cout << map[i][j] << " ";
}
cout << endl;
}
return;
}
void bfs()
{
queue<node>q;//建立一个队列
q.push({0, 0});//起点先入队
while (!q.empty())
{
for (int i = 0; i < 2; i++)
{
int dx = q.front().x + f[i][0];//下一个要搜的x坐标
int dy = q.front().y + f[i][1];//下一个要搜的y坐标
if (map[dx][dy] != '#' && dx >= 0 && dx <= x1 && dy >= 0 && dy <= yy1)
{
q.push({ dx, dy });//满足条件就入队
/*nxt[q.front().x][q.front().y][0] = dx;
nxt[q.front().x][q.front().y][1] = dy;*/
nxt[dx][dy][0] = q.front().x;
nxt[dx][dy][1] = q.front().y;
}
if (dx == x1 && dy == yy1)
{
return;
}
}
q.pop();
}
cout << "No path!" << endl;
return;
}
int main()
{
cin >> x1 >> yy1 >> x2 >> y2;
//初始化地图
for (int i = 0; i <= x1; i++)
{
for (int j = 0; j <= yy1; j++)
{
map[i][j] = '.';
}
}
//把马及马能走到的地方的点标记
map[x2][y2] = '#';
map[x1][x1] = '*';
for (int i = 0; i < 8; i++)
{
int tmpx = x2 + hf[i][0], tmpy = y2 + hf[i][1];
if (tmpx >= 0 && tmpx <= x1 && tmpy >= 0 && tmpy <= yy1)
{
map[tmpx][tmpy] = '#';//障碍
}
}
//map_print();
nxt[0][0][0] = -1, nxt[0][0][1] = -1;
bfs();
print(x1, yy1);
map_print();
return 0;
}