前缀和&差分
一维前缀和
问题描述:
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
前缀和是一种重要的预处理,能大大降低查询的时间复杂度。可以简单理解为“数列的前n项的和”
用法: O(1)求得一维连续子数组的和
状态定义:
1.
A
[
i
]
A[i]
A[i]:原数组下标为i的值
2.
B
[
i
]
B[i]
B[i]表示A数组(1-i)子数组的和
预处理:利用递推关系
B
[
i
]
=
B
[
i
?
1
]
+
A
[
i
]
B[i]=B[i-1]+A[i]
B[i]=B[i?1]+A[i]求得B数组
void presum(int N,int A[])
B[0] = A[0];
for (int i = 1; i < N; i++)
B[i] = B[i - 1] + A[i];
获得连续子数组和
获取从下标从l到下标为r的和
int getSubsum(int l,int r)
{
return B[r]-B[l-1];
}
//完整代码
#include<iostream>
using namespace std;
int num[100005];
int sum[100005];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
scanf("%d",&num[i]);
sum[i]=num[i]+sum[i-1];
}
while(m--)
{
int l,r;
cin>>l>>r;
printf("%d\n",sum[r]-sum[l-1]);
}
return 0;
}
二维前缀和
问题描述
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
用法: O(1)求得二维子矩阵的和
状态定义
1.A[i][j]原数组下标为i,j的初始值
2.B[i][j]表示左上角为(1,1)右下角为(i,j)的子矩阵和
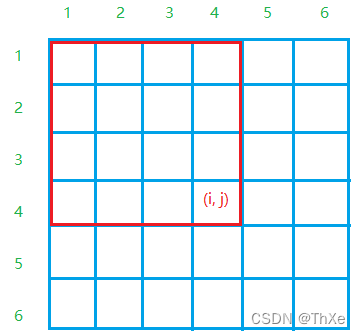
递推关系:
B
[
i
]
[
j
]
=
A
[
i
]
[
j
]
+
B
[
i
?
1
]
[
j
]
+
B
[
i
]
[
j
?
1
]
?
B
[
i
?
1
]
[
j
?
1
]
;
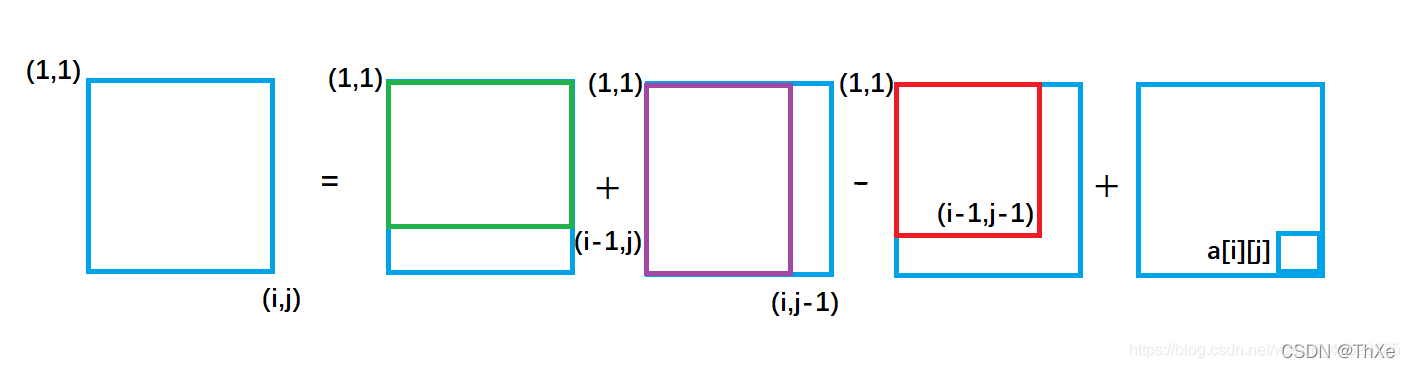
B[i][j]=A[i][j]+B[i-1][j]+B[i][j-1]-B[i-1][j-1];
B[i][j]=A[i][j]+B[i?1][j]+B[i][j?1]?B[i?1][j?1];
整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j]
预处理
void presum(int n,int m)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
B[i][j]=A[i][j]+B[i-1][j]+B[i][j-1]-B[i-1][j-1];
}
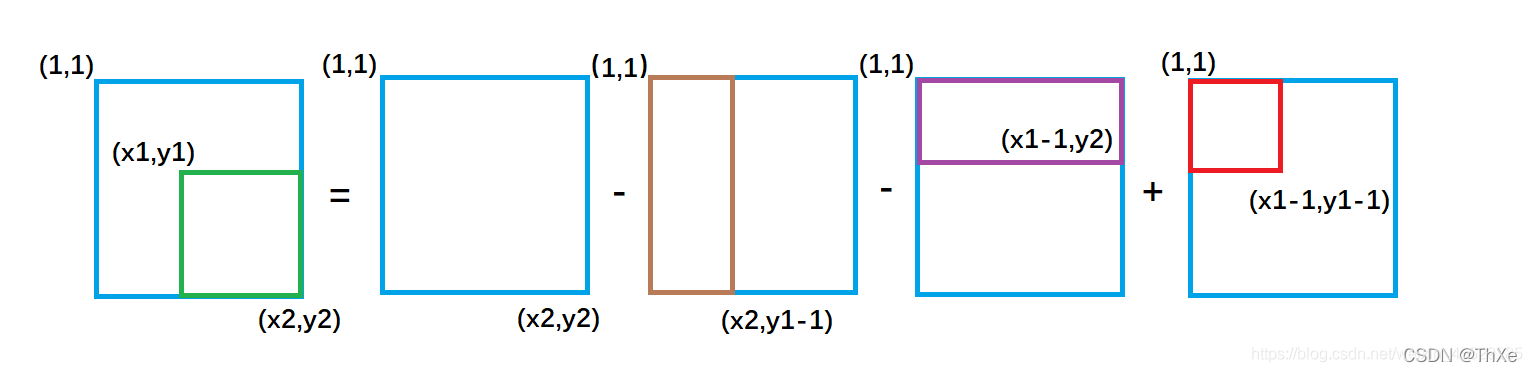
获得左上角为(x1,y1)右下角为(x2,y2)的子矩阵和
int getSubMar(int x1,int y1,int x2,int y2)
{
return B[x2][y2]-B[x2][y1-1]-B[x1-1][y2]+B[x1-1][y1-1]
}
//完整代码
#include<iostream>
using namespace std;
int num[1005][1005],sum[1005][1005];
int main()
{
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&num[i][j]);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
sum[i][j]=num[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}
while(q--)
{
int x1,x2,y1,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]);
}
}

差分
问题描述:
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。

用法:维护多次对序列的一个区间加上一个数,并在最后O(1)求出某一位的数或是多次询问某一位的数,一般配合前缀和使用
状态定义
1.
A
[
i
]
:
原
数
组
下
标
为
i
的
值
A[i]:原数组下标为i的值
A[i]:原数组下标为i的值
2.
B
[
i
]
表
示
A
数
组
经
过
修
改
后
的
数
组
B[i]表示A数组经过修改后的数组
B[i]表示A数组经过修改后的数组
构造差分数组
void(int n)
{
for(int i=1;i<=n;i++)
{ B[i]+=A[i];
B[i+1]-=A[i];
}
}
对原数组进行区间[l,r]+c
void add(int l,int r,int c)
{
B[l]+=k;
B[r+1]-=k;
}
通过前缀和得到修改后的数组,返回数组位置为id的值
int get(int id)
{
for(int i=1;i<=n;i++)
B[i]+=B[i-1];
return B[id];
}
完整代码
#include<iostream>
using namespace std;
int num[100005],a[100005];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
{
num[i]+=a[i];
num[i+1]-=a[i];
}
int l,r,k;
while(m--)
{
cin>>l>>r>>k;
num[l]+=k;
num[r+1]-=k;
}
for(int i=1;i<=n;i++)
num[i]+=num[i-1];
for(int i=1;i<=n;i++)
cout<<num[i]<<" ";
return 0;
}
二维差分
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
状态定义:
1.
A
[
i
]
[
j
]
:
原
数
组
下
标
为
(
i
,
j
)
的
值
A[i][j]:原数组下标为(i,j)的值
A[i][j]:原数组下标为(i,j)的值
2.
B
[
i
]
[
j
]
表
示
A
数
组
经
过
修
改
后
的
二
维
数
组
(
i
,
j
)
的
值
B[i][j]表示A数组经过修改后的二维数组(i,j)的值
B[i][j]表示A数组经过修改后的二维数组(i,j)的值
单次修改
void add(int x1, int y1, int x2, int y2, int c) {
ans[x1][y1] += c;
ans[x2 + 1][y1] -= c;
ans[x1][y2 + 1] -= c;
ans[x2 + 1][y2 + 1] += c;
}
得到答案
void Ans(int n,int m)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{ ans[i][j]+=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
cout<<ans[i][j]<<" ";
}
cout<<endl;
}
}
完整代码
#include<iostream>
using namespace std;
int num[1005][1005],ans[1005][1005];
void add(int x1, int y1, int x2, int y2, int c) {
ans[x1][y1] += c;
ans[x2 + 1][y1] -= c;
ans[x1][y2 + 1] -= c;
ans[x2 + 1][y2 + 1] += c;
}
int main()
{ int n,m,q;
cin>>n>>m>>q;
int i,j;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
cin>>num[i][j];
add(i, j, i, j, num[i][j]);
}
while(q--)
{
int x1,x2,y1,y2,k;
cin>>x1>>y1>>x2>>y2>>k;
add(x1,y1,x2,y2,k);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{ ans[i][j]+=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
cout<<ans[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
