目录
1. 奖券数目(结果填空)
有些人很迷信数字,比如带“4”的数字,认为和“死”谐音,就觉得不吉利。
虽然这些说法纯属无稽之谈,但有时还要迎合大众的需求。某抽奖活动的奖券号码是5位数(10000-99999),要求其中不要出现带“4”的号码,主办单位请你计算一下,如果任何两张奖券不重号,最多可发出奖券多少张。
请提交该数字(一个整数),不要写任何多余的内容或说明性文字。
思路:这道题很简单,我这里提供两种做法,方法一直接对范围内的数进行取余,如果等于有一位数等于4则跳过,不等于4则++,方法二将其范围内的数字转化成字符串,用find查找每个数字中是否存在4;
方法一:
#include<iostream>
using namespace std;
int cnt = 0;
bool f(int x)
{
while (x > 0)
{
int m = x % 10;
if (m == 4)
{
return false;
}
x /= 10;
}
return true;
}
int main()
{
for (int i = 10000; i <= 99999; i++)
{
if (f(i))
{
cnt++;
}
}
cout << cnt << endl;
return 0;
}方法二:
#include<iostream>
#include<string>
#include<sstream>
using namespace std;
int ants;
void i2s(int i, string& s)
{
stringstream ss;
ss << i;
ss >> s;
}
int main()
{
for (int i = 10000; i <= 99999; i++)
{
string s;
i2s(i,s);
if (s.find('4') == string::npos)
{
ants++;
}
}
cout << ants << endl;
return 0;
}答案:52488?
2. 星系炸弹(结果填空)
在X星系的广袤空间中漂浮着许多X星人造“炸弹”,用来作为宇宙中的路标。
每个炸弹都可以设定多少天之后爆炸。
比如:阿尔法炸弹2015年1月1日放置,定时为15天,则它在2015年1月16日爆炸。
有一个贝塔炸弹,2014年11月9日放置,定时为1000天,请你计算它爆炸的准确日期。请填写该日期,格式为 yyyy-mm-dd ?即4位年份2位月份2位日期。比如:2015-02-19
请严格按照格式书写。不能出现其它文字或符号。
?思路:因为这是道填空题,我们可以用电脑自带的excel做,还有菜单栏附件那里有个计算器,也可以做这道题,不过最后还是想用代码实现一下
方法一:
方法二:代码实现
#include<iostream>
using namespace std;
class Date {
public:
Date(int year, int month, int day)
{
_year = year;
_month = month;
_day = day;
}
int GetMonthDay(int year, int month)
{
static int monthDayArray[13] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
int day = monthDayArray[month];
// 365天 5小时+
if (month == 2 && ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)))
{
day += 1;
}
return day;
}
Date& operator+=(int day)
{
_day += day;
while (_day > GetMonthDay(_year, _month))
{
_day -= GetMonthDay(_year, _month);
++_month;
if (_month == 13)
{
_month = 1;
_year++;
}
}
return *this;
}
void print()
{
cout << _year << "-" << _month << "-" << _day << endl;
}
private:
int _year;
int _month;
int _day;
};
int main()
{
Date d1(2014, 11, 9);
d1 += 1000;
d1.print();
return 0;
}答案:2017-8-5?
3.??三羊献瑞(结果填空)
观察下面的加法算式:
? ? 祥 瑞 生 辉
?+ 三 羊 献 瑞
?-------------------
三 羊 生 瑞 气(如果有对齐问题,可以参看【图1.jpg】)
其中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字(答案唯一),不要填写任何多余内容。

思路:此题可以用8个for循环进行暴力枚举,反正是填空题,不用考虑效率问题.也可以用STL库中的next_permutation进行全排列,然后再判断是否符合题意;最后一种方法是结合数学思想,减少for循环,提高算法效率
三 -> a -> a[0]
羊 -> b -> a[1]
献 -> c -> a[2]
瑞 -> d -> a[3]
祥 -> e -> a[4]
生 -> f -> a[5]
辉 -> g -> a[6]
气 -> h -> a[7]
方法一:暴力枚举,将八个不同的字母a-h来代替八个汉字
#include<iostream>
#include<bits/stdc++.h>
int main(){
int sum, sum1, sum2;
for(int a=1;a<=9;a++){ //a 不能等于 0
for(int b=0;b<=9;b++){
if(b!=a){
for(int c=0;c<=9;c++){
if(c!=a&&c!=b){
for(int d=0;d<=9;d++){
if(d!=a&&d!=b&&d!=c){
for(int e=1;e<=9;e++){ //e 不能等于 0
if(e!=a&&e!=b&&e!=c&&e!=d){
for(int f=0;f<=9;f++){
if(f!=a&&f!=b&&f!=c&&f!=d&&f!=e){
for(int g=0;g<=9;g++){
if(g!=a&&g!=b&&g!=c&&g!=d&&g!=e&&g!=f){
for(int h=0;h<=9;h++){
if(h!=a&&h!=b&&h!=c&&h!=d&&h!=e&&h!=f&&h!=g){
sum1=e*1000+d*100+f*10+g;
sum2=a*1000+b*100+c*10+d;
sum=a*10000+b*1000+f*100+d*10+h;
if(sum==(sum1+sum2)){
printf("%d\n",sum2);
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
return 0;
}
方法二:使用STL库中的next_permutation全排列;使用数组a来代替字母
// a[4] a[3] a[5] a[6]
//+ a[0] a[1] a[2] a[3]
//------------------------------ -
//a[0] a[1] a[5] a[3] a[7]
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int a[10] = { 0,1,2,3,4,5,6,7,8,9 };
int sum1 = 0;
int sum2 = 0;
int sum = 0;
while (next_permutation(a, a + 10))
{
if (a[0] != 0 && a[4] != 0)
{
sum1 = a[4] * 1000 + a[3] * 100 + a[5] * 10 + a[6];
sum2 = a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3];
sum = a[0] * 10000 + a[1] * 1000 + a[5] * 100 + a[3] * 10 + a[7];
if ((sum1 + sum2) == sum)
{
break;
}
}
}
cout << sum2 << endl;
return 0;
}答案:1085?
4. 格子中的输出(代码填空)
StringInGrid函数会在一个指定大小的格子中打印指定的字符串。
要求字符串在水平、垂直两个方向上都居中。
如果字符串太长,就截断。
如果不能恰好居中,可以稍稍偏左或者偏上一点。
下面的程序实现这个逻辑,请填写划线部分缺少的代码。
#include <stdio.h>
#include <string.h>
void StringInGrid(int width, int height, const char* s)
{
int i,k;
char buf[1000];
strcpy(buf, s);
if(strlen(s)>width-2) buf[width-2]=0;
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
for(k=1; k<(height-1)/2;k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("|");
printf("%*s%s%*s",_____________________________________________); //填空
printf("|\n");
for(k=(height-1)/2+1; k<height-1; k++){
printf("|");
for(i=0;i<width-2;i++) printf(" ");
printf("|\n");
}
printf("+");
for(i=0;i<width-2;i++) printf("-");
printf("+\n");
}
int main()
{
StringInGrid(20,6,"abcd1234");
return 0;
}?对于题目中数据,应该输出:
+------------------+
| ? ? ? ? ? ? ? ? ? ? ? ? ? ? |
| ? ? abcd1234 ? ? ? ?|
| ? ? ? ? ? ? ? ? ? ? ? ? ? ? |
| ? ? ? ? ? ? ? ? ? ? ? ? ? ? |
+------------------+
思路:做这种代码填空题首先,我们把要填的地方注释掉,然后运行看看效果,
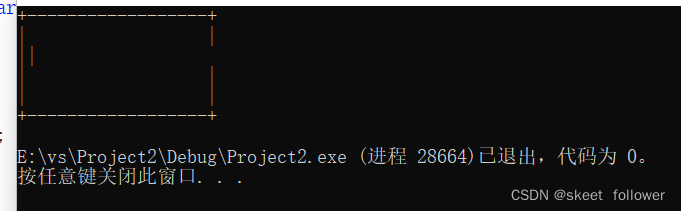
也就是需要我们定位字符的位置,其次看下需要填的代码段
printf("%*s%s%*s",_____________________________________________); ?*s这个考的比较偏,不过没事我们可以查看cplusplus
![]()
?其实就相当于占位符
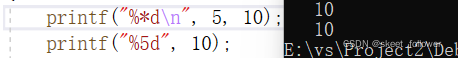
到这里我们知道,也就是宽度width减去字符串的长度再减去2整体除以2就可以得到答案.
答案:(width-2-strlen(buf))/2,"",buf,(width-2-strlen(buf))/2,"")?
5. 九分组分数(代码填空)
1,2,3...9 这九个数字组成一个分数,其值恰好为1/3,如何组法?
下面的程序实现了该功能,请填写划线部分缺失的代码。
#include <stdio.h>
void test(int x[])
{
int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3];
int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8];
if(a*3==b) printf("%d / %d\n", a, b);
}
void f(int x[], int k)
{
int i,t;
if(k>=9){
test(x);
return;
}
for(i=k; i<9; i++){
{t=x[k]; x[k]=x[i]; x[i]=t;}
f(x,k+1);
_____________________________________________ // 填空处
}
}
int main()
{
int x[] = {1,2,3,4,5,6,7,8,9};
f(x,0);
return 0;
}
?思路:其实看过我前面博客的人都知道这是个全排列模板,递归的回溯,直接可以填充答案,
答案:t=x[k];x[k]=x[i];x[i]=t;
6. 加法变乘法(结果填空)
我们都知道:1+2+3+ … + 49 = 1225
现在要求你把其中两个不相邻的加号变成乘号,使得结果为2015比如:
1+2+3+…+10*11+12+…+27*28+29+…+49 = 2015
就是符合要求的答案。请你寻找另外一个可能的答案,并把位置靠前的那个乘号左边的数字提交(对于示例,就是提交10)。
?思路:这道题实际上是枚举,我们需要枚举两个乘号的位置,第一个乘号的位置,从1开始最多到46位置,这样才能保证不相邻并且有第二个乘号.第二个乘号的位置,要与第一个位置间隔开来,所以开始位置应该是第一个乘号位置+2,最多到48那里,也就是最后一个运算符.我们会发现两个表达式除了乘号位置其他位置都一样,可以用等于2015的表达式减去等于1225的表达式。
代码:
#include<iostream>
using namespace std;
int main()
{
for(int i=1;i<=46;i++)
for (int j = i + 2; j <= 48; j++)
{
if (i * (i + 1) - (i + i + 1) + j * (j + 1) - (j + j + 1) == 2015 - 1225)
{
cout << i << " " << j << endl;
}
}
return 0;
}答案:16
7. 牌型种数(结果填空)
小明被劫持到X赌城,被迫与其他3人玩牌。一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。这时,小明脑子里突然冒出一个问题:如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
请填写该整数,不要填写任何多余的内容或说明文字。
?思路:分析题目可以知道这道题目其实一个排列组合问题,需要尝试所有排列组合方案的可能性,根据这个特点我们可以使用递归解决(递归可以搜索的可能性),但是这道题目有一个限制条件是只考虑点数,不考虑牌的顺序,所以在求解的时候不能够像求解全排列那样对于不同的排序方式计算为不同的方案,其实这道题目可以转换为求解每一个数字出现的次数就可以避免牌的出现顺序不同被计数的问题,有的时候换一种思考问题的方式可能会使问题的处理变得简单一点。
代码:
#include <iostream>
#define ll long long
using namespace std;
ll ans = 0;
void dfs(int cnt, int num) {
//拿到十三张牌
if (cnt == 13) ans++;
//牌的数量超过十三张
if (cnt >= 13) return;
//拿到第十四种牌 (当然是不允许的)
if (num > 13) return;
//遍历第num种牌的拿取方式
for (int i = 0; i <= 4; i++) {
dfs(cnt + i, num + 1);
}
}
int main() {
dfs(0, 1);
cout << ans << endl;
return 0;
}
答案:3598180
8. 移动距离(编程题)
X星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为1,2,3…
当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为6时,开始情形如下:1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 …我们的问题是:已知了两个楼号m和n,需要求出它们之间的最短移动距离(不能斜线方向移动)
输入为3个整数w m n,空格分开,都在1到10000范围内
w为排号宽度,m,n为待计算的楼号。
要求输出一个整数,表示m n 两楼间最短移动距离。例如:
用户输入:
6 8 2
则,程序应该输出:
4再例如:
用户输入:
4 7 20
则,程序应该输出:
5资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。提交时,注意选择所期望的编译器类型。
思路:这道题就是考一些数学公式,首先算出来两个数m,n所在的行,这个怎么计算囊?就是m%w,n%w,判断是否等于0,如果等于0,则行数等于rm=m/w,rn=n/w,如果不等于0则rm=m/w+1,rn=n/w+1;其次就是要判断在的列数,因为他们是反方向排号,首先判断是在偶数列还是在奇数列rm%2如果在偶数列,就是rm*w-m+1这个自己带入几个数就直到原因了,如果不在奇数列w-(rm*w-m);同理rn也是如此.
#include<iostream>
using namespace std;
int main()
{
int w, m, n;
cin >> w >> m >> n;
int rm = m % w == 0 ? m / w : m / w + 1;
int rn = n % w == 0 ? n / w : n / w + 1;
int cn = 0, cm = 0;
if (rm % 2 == 0)cm = rm * w - m + 1;
else
cm = w - (rm * w - m);
if (rn % 2 == 0) cn = rn * w - n + 1;
else
cn = w - (rn * w - n);
cout << abs(rm - rn) + abs(cm - cn) << endl;
return 0;
}
9. 垒骰子(编程题)
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。「样例输入」
2 1
1 2「样例输出」
544「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include?, 不能通过工程设置而省略常用头文件。提交时,注意选择所期望的编译器类型。?
思路:这道题我们可以用递归和动态规划做,不过只能得到部分分,重要的是理解这两个思想,后面我们用矩阵解这个题.
方法一:递归
//递归
#include<iostream>
using namespace std;
#define mod 1000000007
int op[7];//记录对立面
bool conflict[7][7];//判断是否冲突
int n, m;
void Init()
{
op[1] = 4;
op[2] = 5;
op[3] = 6;
op[4] = 1;
op[5] = 2;
op[6] = 3;
}
long long int f(int up, int cnt)
{
if (cnt == 0)
{
return 4;
}
long long ants = 0;
for (int upp = 1; upp <= 6; upp++)
{
if (conflict[op[up]][upp])continue;
ants = (ants + f(upp, cnt - 1)) % mod;
}
return ants;
}
int main()
{
Init();
cin >> n >> m;
int x, y;
long long ants = 0;
for (int i = 0; i < m; i++)
{
cin >> x >> y;
conflict[x][y] = true;
conflict[y][x] = true;
}
for (int up = 1; up <= 6; up++)
{
ants = (ants + 4*f(up, n - 1))%mod;
}
cout << ants << endl;
return 0;
}
方法二:动态规划
#include<iostream>
#include<map>
using namespace std;
long long dp[2][7];//dp[i][j]表示有i层,限定朝上的数字为j的稳定方案数
#define mod 1000000007
//int op[7];//记录对立面
bool conflict[7][7];//判断是否冲突
map<int, int>op;
int n, m;
void Init()
{
op[1] = 4;
op[2] = 5;
op[3] = 6;
op[4] = 1;
op[5] = 2;
op[6] = 3;
}
int main()
{
Init();
cin >> n >> m;
int x, y;
long long ants = 0;
for (int i = 0; i < m; i++)
{
cin >> x >> y;
conflict[x][y] = true;
conflict[y][x] = true;
}
//输入完成
for (int j = 1; j <= 6; j++)
{
dp[0][j] = 1;
}
int cur = 0;
//迭代层数
for (int level = 2; level <= n; level++)
{
cur = 1 - cur;
//尝试把6个面放在当前一层朝上的方向
for (int j = 1; j <= 6; j++)
{
dp[cur][j] = 0;
//将与op[j]不冲突的上一层格子里面的数累加起来
for (int i = 1; i <= 6; i++)
{
if (conflict[op[j]][i])continue;//冲突的面朝上是不可取的
dp[cur][j] = (dp[cur][j] + dp[1 - cur][i]) % mod;
}
}
}
long long sum = 0;
for (int k = 1; k <= 6; k++)
{
sum = (sum + dp[cur][k] )% mod;
}
//快速冥求4的次方
long long ans = 1;
long long tmp = 4;
long long p = n;
while (p != 0)
{
if (p & 1 == 1) ans = (ans * tmp) % mod;
tmp = (tmp * tmp) % mod;
p >>= 1;
}
cout << (sum * ans) % mod << endl;
return 0;
}?方法三:矩阵
#include<bits/stdc++.h>
#define ag(x) ((x)>3?(x)-3:(x)+3)
using namespace std;
typedef long long ll;
ll mod=1e9+7;
struct matrix{
int n,m;
ll s[10][10];
};
//对A的初始化修改成 初始化为4,因为骰子四个面可以互相转动,需要最终乘以4或者初始化为4
matrix Aunit(matrix A){
for(int i=0;i<6;i++){
for(int j=0;j<6;j++){
A.s[i][j]=4;
}
}
return A;
}
//返回一个单位矩阵
matrix unit(matrix A){
matrix re;
re.n=A.n;re.m=A.m;
for(int i=0;i<re.n;i++){
for(int j=0;j<re.m;j++){
if(i==j)re.s[i][j]=1;
else re.s[i][j]=0;
}
}
return re;
}
//两个矩阵相乘
matrix mix(matrix A,matrix B){
matrix re;re.n=A.n;re.m=B.m;
for(int i=0;i<re.n;i++){
for(int j=0;j<re.m;j++){
re.s[i][j]=0;
for(int k=0;k<A.m;k++){
re.s[i][j]+=A.s[i][k]*B.s[k][j]%mod;
re.s[i][j]%=mod;
}
}
}
return re;
}
//快速求 矩阵A的b次方
matrix dpow(matrix A,ll b){
matrix re;
re=unit(A);
while(b){
if(b&1)re=mix(re,A);
A=mix(A,A);
b>>=1;
}
return re;
}
int main(){
ll n,m;
scanf("%lld%lld",&n,&m);
matrix A;A.n=6;A.m=6;
A=Aunit(A); //初始化矩阵A,表示冲突矩阵
int ip1,ip2;
//设置冲突矩阵的冲突面(两两对应)
while(m--){
scanf("%d%d",&ip1,&ip2);
A.s[ip2-1][ag(ip1)-1]=0;
A.s[ip1-1][ag(ip2)-1]=0;
}
matrix p;p.n=1;p.m=6;
for(int j=0;j<6;j++)p.s[0][j]=4;
A=dpow(A,n-1); //求A矩阵的n-1次方
p=mix(p,A); //最后算A^n-1矩阵 * p矩阵,(p就是高度为1的第一个矩阵对应dp[1])
ll ans=0;
for(int j=0;j<6;j++)ans=(ans+p.s[0][j])%mod;
printf("%lld\n",ans);
return 0;
}10. 生命之树(编程题)
在X森林里,上帝创建了生命之树。 他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。 上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b} 使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。?
在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。 这个最大的和就是上帝给生命之树的评分。 ?
经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算,他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。 ??
「输入格式」?
第一行一个整数 n 表示这棵树有 n 个节点。 第二行 n 个整数,依次表示每个节点的评分。?
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。由于这是一棵树,所以是不存在环的。 ??
「输出格式」?
输出一行一个数,表示上帝给这棵树的分数。 ??
「样例输入」?5?
1 -2 -3 4 54 2
3 1
1 2
2 5 ??
「样例输出」?8 ??
「数据范围」?
对于 30% 的数据,n <= 10?
对于 100% 的数据,0 < n <= 10^5, 每个节点的评分的绝对值不超过 10^6 。 ??
资源约定:?
峰值内存消耗 < 256M CPU消耗 ?< 3000ms
思路:对于每个结点的决策有2种,分别是选择和不选择,那么我们定义dp[ i ][ 0 ] 和 dp[ i ][ 1 ]分别表示不选择(选择) i 结点能得到的最大权值和。状态转移方程是:dp [ i ] [ 1 ] = sum(max(dp[ j ][ 1 ] , dp[ j ][ 0 ])); ?j 是 i 的孩子结点 ;? ?dp[ i ][ 0 ] = 0;? 由于题目中给出的是无根树,所以在进行DFS的时候要进行标记,当要搜索的结点的孩子结点都曾经被访问过,那么他就是叶节点。也是就递归的边界(停止该分支的搜索)。
#include<cstdio>
#include<cstring>
#include<vector>
#define N 100005
using namespace std;
vector<int> node[N];
// dp[i][0],dp[i][1];
// 分别表示选i结点和不选能得到的最大分数
int dp[N][2];
int v[N],vis[N];
int n,a,b;
void dfs(int u){
dp[u][1] = v[u];
dp[u][0] = 0;
vis[u]=1;
for(int i=0 ;i<node[u].size();i++){
if(!vis[node[u][i]]){
dfs(node[u][i]);
dp[u][1] += max(dp[node[u][i]][1],dp[node[u][i]][0]);
}else{
dp[u][1] = max(dp[u][1],v[u]);
dp[u][0] = max(dp[u][0],0);
}
}
}
void init(){
memset(v,0,sizeof(v));
memset(dp,0,sizeof(dp));
scanf("%d",&n);
for(int i=1 ;i<=n ;i++){
scanf("%d",&v[i]);
}
for(int i=1 ;i<n ;i++){
scanf("%d%d",&a,&b);
node[a].push_back(b);
node[b].push_back(a);
}
}
int main(){
init();
dfs(1);
int ans = -1;
for(int i=1 ;i<=n ;i++){
// printf("dp[%d][1]:%d\n",i,dp[i][1]);
// printf("dp[%d][0]:%d\n",i,dp[i][0]);
ans = max(ans,dp[i][1]);
ans = max(ans,dp[i][0]);
}
printf("%d\n",ans);
return 0;
} 11. 总结
1.奖券的数目? ? ? ? ? ?枚举+字符串查找
2.星系炸弹? ? ? ? ? ? ? ?简单计算
3.三羊献瑞? ? ? ? ? ? ? ?枚举+判断, 数学推理减少未知数
4.格子中输出? ? ? ? ? ?%*s需要两个参:宽度和输出内容
5.九分组分数? ? ? ? ? ?递归求全排列
6.加法变乘法? ? ? ? ? ?枚举 ,巧算
7.牌型种数? ? ? ? ? ? ? ?递归
8.移动距离? ? ? ? ? ? ? 通过举例来找到符号化公式
9.垒骰子? ? ? ? ? ? ? ? ?矩阵运算
10.生命之树? ? ? ? ? ?无限树转有根数,DFS,维护每个节点作为根时能得到的最大权和