[C++知识库]C. Jury Meeting (Educational Codeforces Round 113)

C. Jury Meeting

题意

n个人，个人都有ai个事件要说，当轮到某个人的时候，如果他现在有需要说的事，那就给他的ai减1，如果没有需要说的了，就往下轮，直到所有人都说完了，这过程中不能同一个人说两次

思路

三种情况

1、当最大值的数存在两个的时候，结果为n！，任意排列
2、当最大值-1这个数不存在的时候 结果为0
3、当最大值与最大值-1都存在，符合答案的情况是最大值在至少一个次大值前面

怎么计算第三种情况？

让全部情况数即n! 减 最大值在最后的情况。
最大值和次大值以外的数的顺序无所谓，不需要考虑位置。
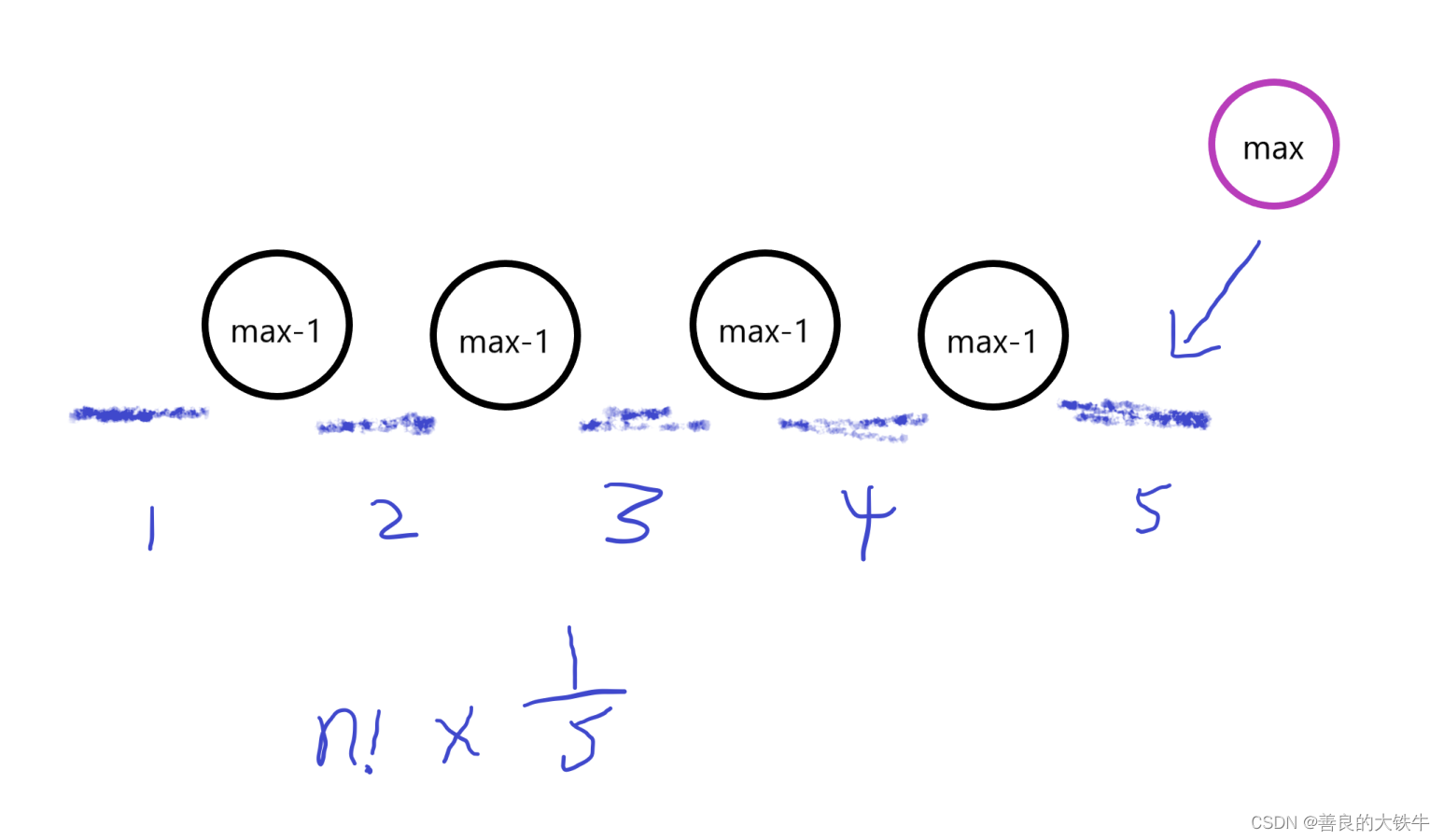
假设现在有次大值k个，根据插空原理可以产生k+1个空位，那么最大值排在最后一个空位的概率就是 1/(k+1)，所以不合法的情况数量就是 n!/(k+1) 。最后总方案数就是 n! - n!/(k+1)。

图示：

代码

#include <iostream>
#include <cstring>
#include <set>
#include <algorithm>
#include <cmath>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <sstream>
using namespace std;
#define endl "\n"
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
#define int long long

const int mod = 998244353;
const int N = 1e5 + 10;
int a[N];               

void solve()
{
    int n;
    cin >> n;
    vector<int> a(n);
    for(int &x : a) cin >> x;
    int mx = *max_element(a.begin(), a.end());
    int cmx = count(a.begin(), a.end(), mx);
    int k = count(a.begin(), a.end(), mx - 1);
    int ans = 1, sum = 1;
    for(int i = 1; i <= n; i ++)
    {
        // n!
        ans = ans * i % mod;
        // 少一个(k+1)  mx-1的数量+1
        if(i != k + 1) sum = sum * i % mod;
    }
    if(cmx == 1) ans = (ans - sum + mod) % mod;
    cout << ans << endl;
}

signed main()
{
    int ________________________________________________________________________;
    cin >> ________________________________________________________________________;
    while (________________________________________________________________________--)
    {
        solve();
    }
}