BF算法
字符串:“abcd”
真子串:’ ‘,‘a’,‘b’,‘c’,‘d’,‘ab’,‘bc’,‘cd’,‘abc’,‘bcd’ ?(1+n)*n/2
子串:’ ',‘a’,‘b’,‘c’,‘d’,‘ab’,‘bc’,‘cd’,‘abc’,‘bcd’,‘abcd’ ? (1+n)*n/2+1
主串:“ababcabcdabcde” ? pos 0 return 5(pos代表主串所指向字母的下标,return代表遇到和子串一致的主串中的元素下标)
子串:"abcd’? pos 7 return 9
BF算法:暴力求解
主串:“ababcabcdabcde”?i指向主串的第一个位置
子串:"abcd’?j指向子串的第一个位置
1.第一种BF算法(这种是错误的)
如果i和j指向的字符相同,则i++,j++;
如果i和j指向的字符不相同,则j=0,重新开始比较;
退出条件:当i或者j向后走,越界了
看子串在主串中找到没找到只用看j即可,j如果走出自身范围,则找到了,否则没找到,如果找到,返回i-j
但是有一个例子:
主串:“aaaaaaaaaaaaab”
子串:“aaaaaaaaaaaab”
此时第一种b=BF算法是不适用的,所以是错误的。
1.第二种BF算法
如果i和j指向的字符相同,则i++,j++;
如果i和j指向的字符不相同,则i=i-j+1,j=0;
退出条件:当i或者j走出自身范围(越界)
退出之后,需要判断到底子串在主串中是否出现,只需要判断j即可
j如果走出自身范围,则找到了,return i-j;
j如果没有走出自身范围,则没有找到,return -1;
2.BF算法代码实现
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <string.h>
//BF算法 时间复杂度O(n*m)
int BF_Search(const char *str, const char *sub, int pos)//pos代表主串向后搜索的开始位置
{
assert(str!=NULL && sub!=NULL && pos>=0 && pos<strlen(str));
int i = pos;
int j = 0;
int len_str = strlen(str);//len_str保存主串有效长度
int len_sub = strlen(sub);//len_sub保存子串有效长度
while(i<len_str && j<len_sub)
{
if(str[i] == sub[j])
{
i++;
j++;
}
else
{ //注意:i和j修改顺序不能颠倒
i = i-j+1; //i回退到这一趟开始位置,的下一个位置继续去比较
j = 0; //j回退到0
}
}
//此时,当while退出,肯定要么找到,要么没找到,只需要通过j判断即可
if(j < len_sub)//j没有走出自身边界,则没找到
{
return -1;
}
else
{
return i-j;
}
}
int main()
{
const char* str = "ababcabcdabcde";
const char* sub = "abcd";
int tmp = BF_Search(str, sub, 3);
if (tmp >= 0)
{
printf("找到了,开始下标为%d\n", tmp);
}
else
{
printf("没有找到\n");
}
return 0;
}
3.运行结果
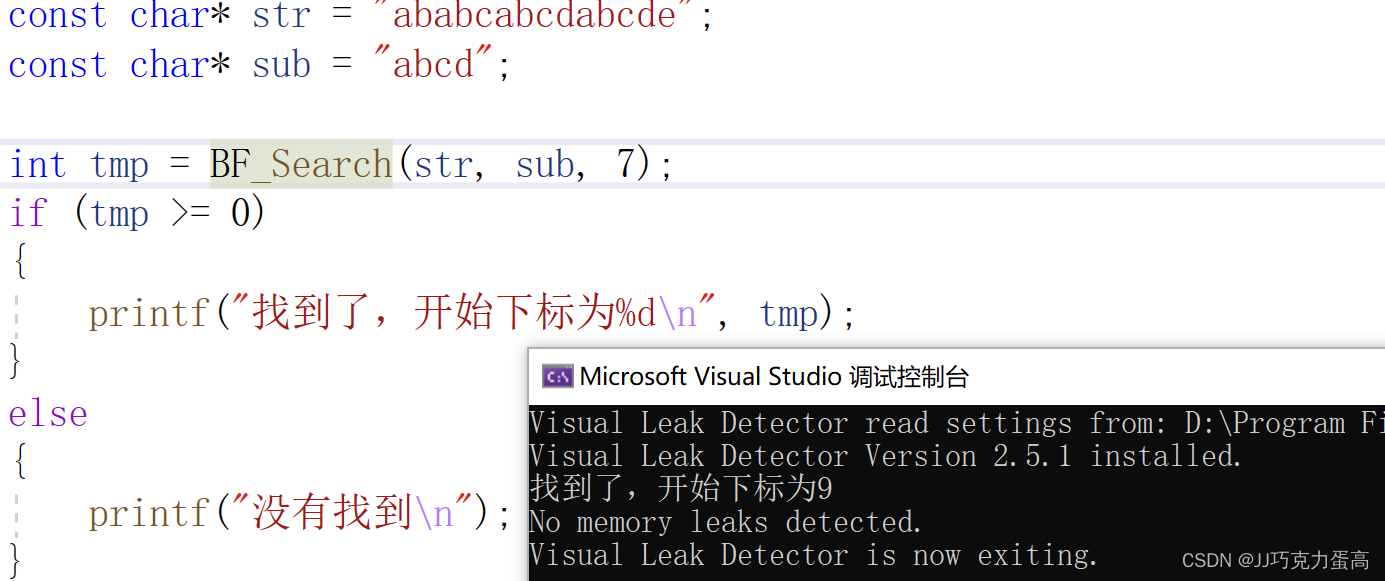

4.BF算法复杂度
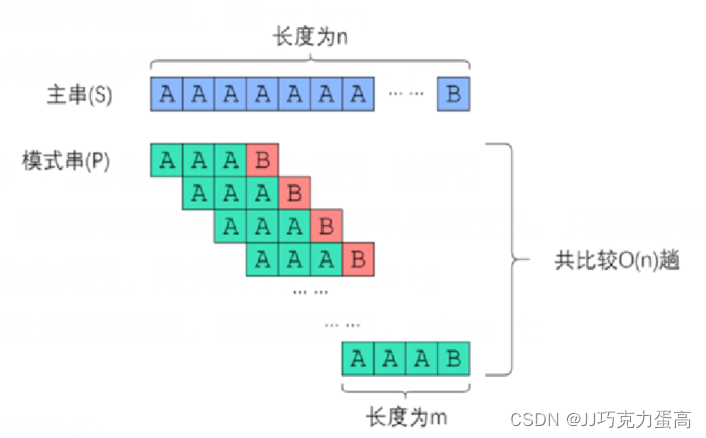
所以,BF算法的时间复杂度为O(n*m)
BF算法的优缺点:
优点: 逻辑简单,实现也简单
缺点: 效率很低,时间复杂度O(n*m)
KMP算法
1.核心思想: i绝不后退
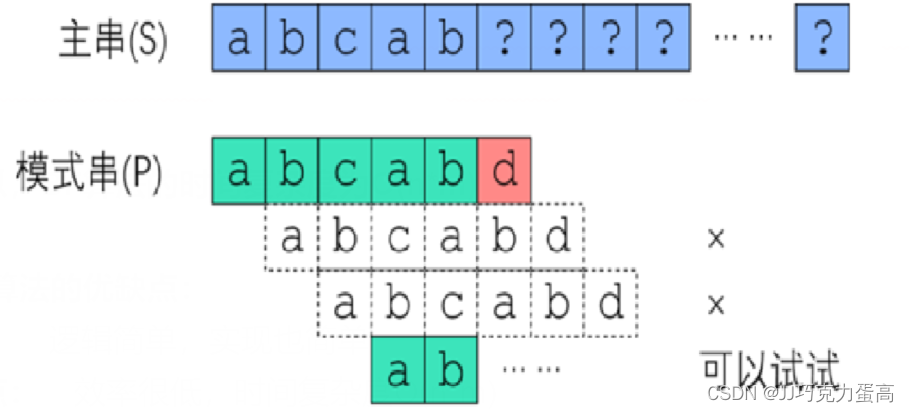
此时,发生了失配,然后通过观察可以得知,失配前已经匹配成功的那些字符,存在两种情况:
1.互相不相等的情况下,i就可以不用回退(i就算回退了,也肯定会失败)
过程如下:
例1:

例2:

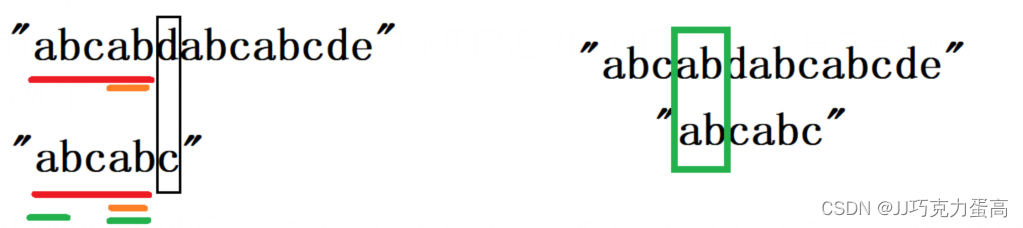
上述说道,如果发生失配时,失配前的字符串互不相等,i可以不用回退;
如果发生失配时,失配前的字符串互有相等情况,i可能需要向前回退,只不过,我们只要证明 左绿那条线 和 上橙那条线 相等,那么i也就可以不用回退,而是让j不再回退到0,而是回退到一个合适的位置,去代替掉
现在重点就在:需要去证明左绿和.上橙相等(因为橙色上下两条线铁定相等,那么我们只需要关注子串即可,证明左绿和右绿存在即可)(证明左绿和上橙相等可以用证明左绿和右绿相等代替掉)
2.代码实现
//求子串的模式匹配串next
int* Get_Next(const char* sub)
{
assert(sub != NULL);
int len = strlen(sub);
int* next = (int*)malloc(len * sizeof(int));
assert(next != NULL);
next[0] = -1;
next[1] = 0;
int j = 1;//通过已知推位置 j代表已知位置 j+1代表要推的未知位置
int k = next[1];
while (j + 1 < len)
{
if (k == -1 || sub[j] == sub[k])//如果当前字符和回退的字符相等 将k+1赋值给下一个位置
{ //或者k==-1,触底了,也是将k+1赋值给下一个位置
k++;
j++;
next[j] = k;
}
else
{
k = next[k];
}
}
return next;
}
//KMP算法的主串,由于i打死不回退,只会遍历一遍 整体时间复杂度O(n+m)
int KMP_Search(const char* str, const char* sub, int pos)
{
assert(str != NULL && sub != NULL && pos >= 0 && pos < strlen(str));
int i = pos;
int j = 0;
int len_str = strlen(str);//len_str保存主串有效长度
int len_sub = strlen(sub);//len_sub保存子串有效长度
int* next = Get_Next(sub);//此时,子串的模式匹配串获取到
while (i < len_str && j < len_sub)
{
if (j == -1 || str[i] == sub[j])//j如果在第一个字符就失配,这时,只能让i向后走一步i++,j应该指向开始位置(0),但是j现在值是-1,要变成0需要j++
{ //或者i和j指向的字符相等也是i++,j++
i++;
j++;
}
else
{
//kmp要求i打死不同回退,j回退到一个合适的位置
j = next[j];
//i = i-j+1; //i回退到这一趟开始位置,的下一个位置继续去比较
//j = 0; //j回退到0
}
}
//此时,当while退出,肯定要么找到,要么没找到,只需要通过j判断即可
if (j < len_sub)//j没有走出自身边界,则没找到
{
return -1;
}
else
{
return i - j;
}
}
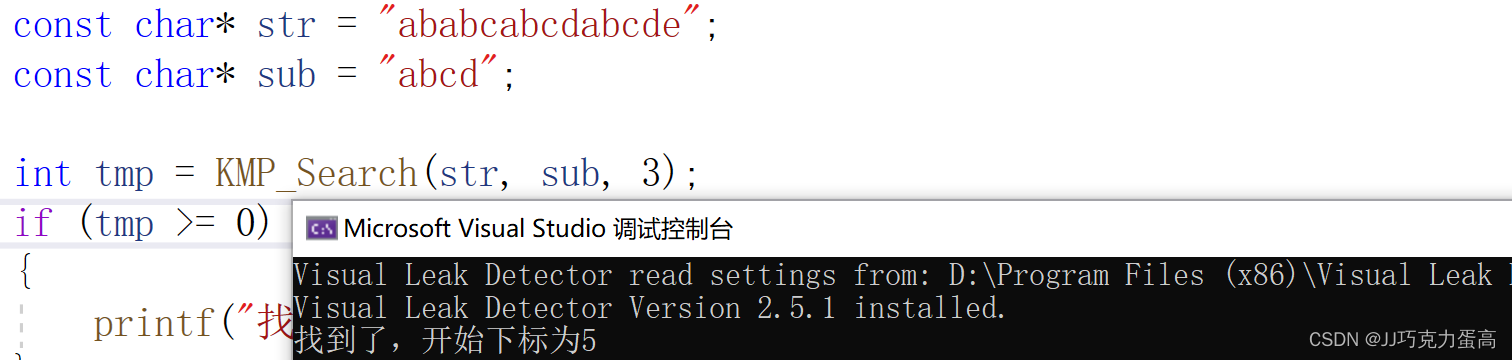
int main()
{
const char* str = "ababcabcdabcde";
const char* sub = "abcd";
int tmp = KMP_Search(str, sub, 3);
if (tmp >= 0)
{
printf("找到了,开始下标为%d\n", tmp);
}
else
{
printf("没有找到\n");
}
return 0;
}
3.运行结果
4.复杂度分析
KMP算法的时间复杂度为:O(n+m)