在求解计数类DP问题时,通常要找到一个"基准点",围绕这一基准点构造一个不可划分的"整体",以避免子问题的重叠.用一个字概括就是, "不重不漏".
例题一:
由于直接计算合法路径过于困难(数据大),我们从反面考虑,我们求出经过黑色格子的路径总数,再从总方案数减去非法的方案数即可.
我们假设左上角和右下角的方格也是黑色格子,再对所有的黑色格子的坐标按照从小到大排序(横坐标和纵坐标).
假设F[i]为从左上角走到排序后的第i个黑色格子,并且途中不经过其他格子的路线数.
有:
为什么这么设计状态呢 ?首先,我们这样设计状态不会重叠,因为第一个经过的黑色格子不同,路径也一定不同.其次,我们枚举了所有的点(之前阶段的点)作为第一个经过的点,一定不会漏掉情况.
初值F[0] = 1, 最终的解F[n + 1].
#include <bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
const int N = 2010, M = 200010, MOD = 1e9 + 7;
int h, w, n;
pair<int, int> cor[N];
int f[N];
int fac[M], inv[M];
int qmi(int a, int k, int p){
int ans = 1;
while (k){
if (k & 1)
ans = ans * a % p;
k >>= 1;
a = a * a % p;
}
return ans;
}
void prework(){
inv[0] = inv[1] = 1;
fac[0] = fac[1] = 1;
for (int i = 2; i <= 200010; ++i){
fac[i] = (fac[i - 1] * i) % MOD;
inv[i] = qmi(fac[i], MOD - 2, MOD);
}
}
int C(int n, int m){
return fac[n] * inv[m] % MOD * inv[n - m] % MOD;
}
signed main(){
cin >> h >> w >> n;
for (int i = 1; i <= n; ++i)
cin >> cor[i].x >> cor[i].y;
sort(cor + 1, cor + n + 1);
cor[n + 1].x = h, cor[n + 1].y = w;
prework();
for (int i = 1; i <= n + 1; ++i){
int sum = 0;
for (int j = 1; j < i; ++j){
if (cor[j].x > cor[i].x || cor[j].y > cor[i].y)
continue;
sum = (sum + f[j] * C(cor[i].x - cor[j].x + cor[i].y - cor[j].y, cor[i].x - cor[j].x)) % MOD;
}
f[i] = C(cor[i].x + cor[i].y - 2, cor[i].x - 1) - sum;
}
cout << (f[n + 1] + MOD) % MOD << "\n";
}例题二:
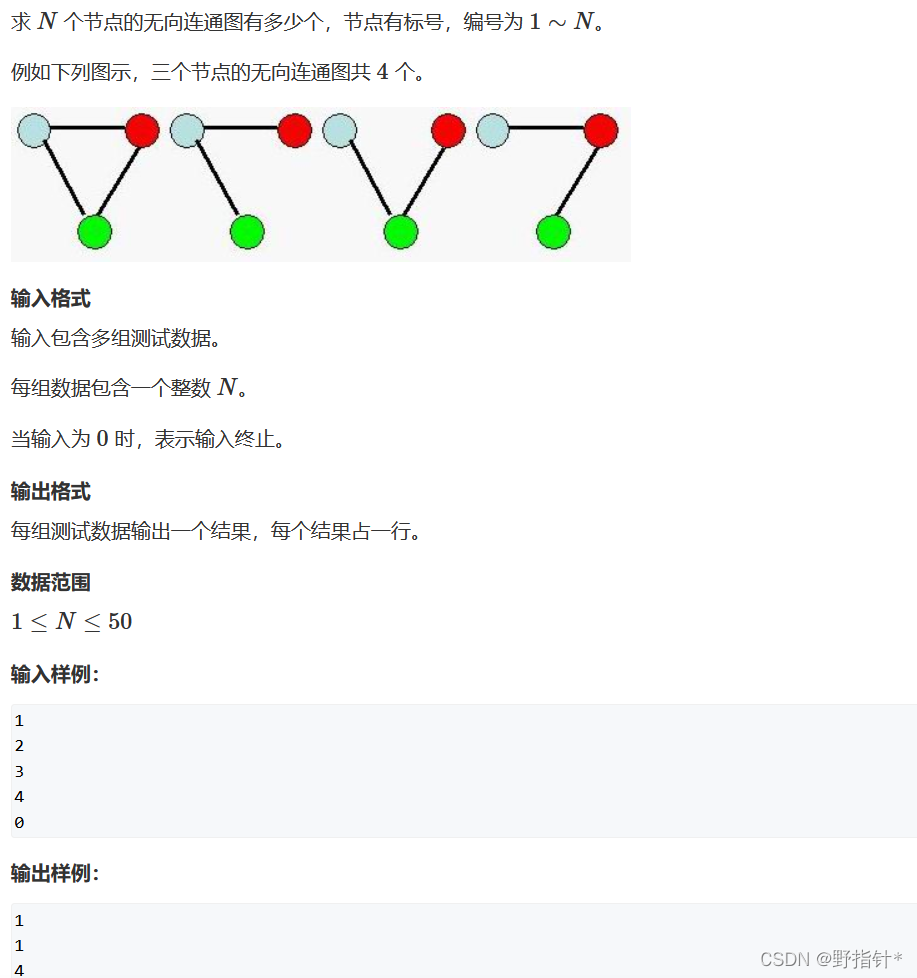
要直接求连通图很难,因为我们不容易划分子问题.所以我们从反面考虑,而一个不连通图则很容易划分为两个节点更少的两部分.
?n个节点构成一张无向图的方案数是:,因为n个节点最多连(n - 1) * n / 2条边,每条边选或者不选.
接下来计算n个点不连通图的无向图的数量,一张不连通的无向图一定由若干个连通块组成,我们枚举标号为1的节点所在的连通块的节点的个数为k,从2 ~ N这N - 1个节点中选取k - 1个节点与1号节点组成连通块,显然有种选法,剩余N - k个节点构成无向图.
假设F[i]为i个节点的无向连通图的个数,有:
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 110;
const int M = 1100;
int n, m, i, j, k;
struct bign{
int a[M], len;
} f[N], power[N];
inline bign operator/(const bign &x, const int y){
bign now;
memset(now.a, 0, sizeof now.a);
now.len = 0;
int ns = 0;
for (int i = x.len; i >= 1; i--){
ns = ns * 10 + x.a[i];
now.a[i] = ns / y;
ns %= y;
if (!now.len && now.a[i])
now.len = i;
}
return now;
}
inline bign operator+(const bign &x, const bign &y){
bign now;
memset(now.a, 0, sizeof now.a);
for (int i = 1; i <= max(x.len, y.len); i++){
now.a[i] += x.a[i] + y.a[i];
now.a[i + 1] = now.a[i] / 10;
now.a[i] %= 10;
}
now.len = max(x.len, y.len);
if (now.a[now.len + 1])
now.len++;
return now;
}
inline bign operator*(const bign &x, const bign &y){
bign now;
memset(now.a, 0, sizeof now.a);
for (int i = 1; i <= x.len; i++)
for (int j = 1; j <= y.len; j++)
{
now.a[i + j - 1] += x.a[i] * y.a[j];
now.a[i + j] += now.a[i + j - 1] / 10;
now.a[i + j - 1] %= 10;
}
now.len = x.len + y.len - 1;
if (now.a[now.len + 1])
now.len++;
return now;
}
inline bign C(int x, int y){
bign tot, temp;
tot.len = 1;
tot.a[1] = 1;
for (int i = y, j = 1; j <= x; i--, j++)
{
int t = i;
temp.len = 0;
while (t)
{
temp.a[++temp.len] = t % 10;
t /= 10;
}
tot = tot * temp / j;
}
return tot;
}
inline void print(const bign &x){
for (int i = x.len; i >= 1; i--)
printf("%d", x.a[i]);
printf("\n");
}
inline void init(){
for (int i = 1; i <= 50; i++)
{
ll temp = ((ll)(1) << i) - 1;
while (temp)
{
power[i].a[++power[i].len] = temp % 10;
temp /= 10;
}
}
f[1].len = 1;
f[1].a[1] = 1;
f[2].len = 1;
f[2].a[1] = 1;
for (int i = 3; i <= 50; i++)
for (int j = 1; j <= i - 1; j++)
f[i] = f[i] + C(j - 1, i - 2) * f[j] * f[i - j] * power[j];
}
int main(){
init();
while (scanf("%d", &n) && n)
print(f[n]);
return 0;
}总结:
1.计数类DP最重要的是不重不漏,这对我们分解问题的要求很高.一般来说,将问题分解成两部分,一部分是固定不变的部分,一部分是变化的.原因有二,第一是这样划分状态不会重复,因为固定部分不同时,两个方案一定不同,变化部分怎么变都行;其次是这样不容易遗漏情况,因为固定部分通常只有一个,我们枚举固定部分的所有情况时较容易.在上面两道例题中,我们也是这样解决问题的.
2.在计数类DP中,还有一个很重要的思想,就是正难则反,当一个问题难以被划分的时候,我们不妨从反面考虑
3.n个节点最多可以构成(n - 1) * n / 2张不同的无向图.