关于C++ STL中的upper_bound()
前言
总所周知😄,C++的upper_bound()函数是查找一个非减序列中位于指定元素后的第一个元素的函数。查找网上资料,发现该函数是通过二分查找实现的 O log ? n {\mathcal{O}\log{n}} Ologn。但是,upper_bound()查找的元素集合可以是链表(比如,下面代码是可以执行的):
#include <iostream>
#include <algorithm>
#include <list>
using namespace std;
int main() {
list<int> a{ 1, 2, 3, 4, 5, 6 };
cout << *upper_bound(a.begin(), a.end(), 3);
}
那么问题来了,链表要怎么进行二分查找?链表中的元素物理地址不是连续的,而二分查找的关键是利用物理地址连续的特点,用 O ( 1 ) \mathcal{O}(1) O(1)的时间找到第 ( l e f t + r i g h t ) / 2 (left+right)/2 (left+right)/2个元素。
为此,我查找了STL源码。
原理
基本原理
- 对于存储地址连续的元素集合:利用 O ( 1 ) \mathcal{O}(1) O(1)的时间找到第 ( l e f t + r i g h t ) / 2 (left+right)/2 (left+right)/2个元素;
- 对于存储地址不连续的元素集合:从 l e f t left left向后遍历 ( l e f t + r i g h t ) / 2 (left+right)/2 (left+right)/2个元素,找到第 ( l e f t + r i g h t ) / 2 (left+right)/2 (left+right)/2个元素;
源码
upper_bound
// FUNCTION TEMPLATE upper_bound
template <class _FwdIt, class _Ty, class _Pr>
_NODISCARD _CONSTEXPR20 _FwdIt upper_bound(_FwdIt _First, _FwdIt _Last, const _Ty& _Val, _Pr _Pred) {
// find first element that _Val is before
_Adl_verify_range(_First, _Last);
auto _UFirst = _Get_unwrapped(_First);
_Iter_diff_t<_FwdIt> _Count = _STD distance(_UFirst, _Get_unwrapped(_Last));
while (0 < _Count) { // divide and conquer, find half that contains answer
_Iter_diff_t<_FwdIt> _Count2 = _Count / 2;
const auto _UMid = _STD next(_UFirst, _Count2);
if (_Pred(_Val, *_UMid)) {
_Count = _Count2;
} else { // try top half
_UFirst = _Next_iter(_UMid);
_Count -= _Count2 + 1;
}
}
_Seek_wrapped(_First, _UFirst);
return _First;
}
-
_First、_Last:首元素和尾元素的迭代器;
-
_UFirst、_UMid:首元素和mid元素的迭代器指针;
-
_Count:_UFirst和**_UMid**之间距离;
-
_Count2:_Count距离一半;
-
第5行:验证**_First和_Last**是否构成一个区间(防止死循环);
-
第7行:获取**_First和_Last**之间的元素个数,distance源码见下面;
-
第11行:获取mid元素的指针;
-
第9-18行:经典的二分法逻辑:
如果mid值【_UMid】和目标值*_Val**,满足条件**_Pred**:
- 将**_UFirst和_UMid**距离缩短到一半,相当于【right = mid】;
否则:
- _UFirst设为**_UFirst**下一个元素,相当于【left = mid + 1】;
- _Count重新赋值,让**_UFirst**+_Count的位置不变,相当于【right位置不变】;
distance
template <class _InIt>
_NODISCARD _CONSTEXPR17 _Iter_diff_t<_InIt> distance(_InIt _First, _InIt _Last) {
if constexpr (_Is_random_iter_v<_InIt>) {
return _Last - _First; // assume the iterator will do debug checking
} else {
_Adl_verify_range(_First, _Last);
auto _UFirst = _Get_unwrapped(_First);
const auto _ULast = _Get_unwrapped(_Last);
_Iter_diff_t<_InIt> _Off = 0;
for (; _UFirst != _ULast; ++_UFirst) {
++_Off;
}
return _Off;
}
}
功能:获取**_First和_Last**之间元素个数。
IF判断集合中元素地址是否是连续的:
如果是的:
- 直接返回地址的差值;
否则:
- 遍历查找元素个数;
advance
template <class _InIt, class _Diff>
_CONSTEXPR17 void advance(_InIt& _Where, _Diff _Off) { // increment iterator by offset
if constexpr (_Is_random_iter_v<_InIt>) {
_Where += _Off;
} else {
if constexpr (is_signed_v<_Diff> && !_Is_bidi_iter_v<_InIt>) {
_STL_ASSERT(_Off >= 0, "negative advance of non-bidirectional iterator");
}
decltype(auto) _UWhere = _Get_unwrapped_n(_STD move(_Where), _Off);
constexpr bool _Need_rewrap = !is_reference_v<decltype(_Get_unwrapped_n(_STD move(_Where), _Off))>;
if constexpr (is_signed_v<_Diff> && _Is_bidi_iter_v<_InIt>) {
for (; _Off < 0; ++_Off) {
--_UWhere;
}
}
for (; 0 < _Off; --_Off) {
++_UWhere;
}
if constexpr (_Need_rewrap) {
_Seek_wrapped(_Where, _STD move(_UWhere));
}
}
}
功能:从**_Where处获取到第_Off**个元素。
IF判断集合中元素地址是否是连续的:
如果是的:
- 直接返回地址加上距离;
否则:
- 遍历查找元素个数(根据**_Off**符号,向前或向后遍历);
复杂度分析
-
对于长度为 n n n的地址连续集合,其时间复杂度为 O ( log ? n ) \mathcal{O}(\log{n}) O(logn)
-
对于长度为 n n n的地址不连续集合,其时间复杂度为
O ( n ) = n 2 + n 4 + n 8 + … \mathcal{O}(n)=\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+ \dots O(n)=2n?+4n?+8n?+…
实验
以下实验为验证对于长度为 n n n的地址不连续集合,其时间复杂度为 O ( n ) \mathcal{O}(n) O(n)
实验代码
#include <iostream>
#include <algorithm>
#include <list>
#include <vector>
using namespace std;
int main() {
clock_t start, finish;
for (int i = 1; i <= 100; i++)
{
list<int> a(100000 * i, 0);
start = clock();
upper_bound(a.begin(), a.end(), 3);
finish = clock();
cout << finish - start << ",";
}
}
实验原始数据
13,29,39,51,73,71,86,95,112,127,130,143,153,164,179,195,202,211,224,240,247,266,275,282,295,307,320,327,344,358,369,382,389,398,415,429,439,444,465,482,482,496,521,518,534,545,566,571,589,591,603,616,627,640,650,659,674,685,700,720,725,730,745,756,769,775,818,813,830,831,846,861,869,877,886,904,927,927,941,956,966,970,995,1061,1085,1110,1105,1118,1124,1139,1144,1178,1103,1114,1122,1136,1149,1152,1168,1187
绘图代码
from matplotlib import pyplot
import matplotlib
x = [i * 100000 for i in range(1, 101, 1)]
y = [13,29,39,51,73,71,86,95,112,127,130,143,153,164,179,195,202,211,224,240,247,266,275,282,295,307,320,327,344,358,369,382,389,398,415,429,439,444,465,482,482,496,521,518,534,545,566,571,589,591,603,616,627,640,650,659,674,685,700,720,725,730,745,756,769,775,818,813,830,831,846,861,869,877,886,904,927,927,941,956,966,970,995,1061,1085,1110,1105,1118,1124,1139,1144,1178,1103,1114,1122,1136,1149,1152,1168,1187]
matplotlib.rcParams['font.family']='STSong'
matplotlib.rcParams['font.size']=20
pyplot.title("list链表长度与upper_bound消耗时间图")
pyplot.grid()
pyplot.ylabel("消耗时间/单位(1)")
pyplot.xlabel("链表长度/单位(1)")
pyplot.scatter(x, y)
pyplot.plot(x, y)
pyplot.show()
可视化结果
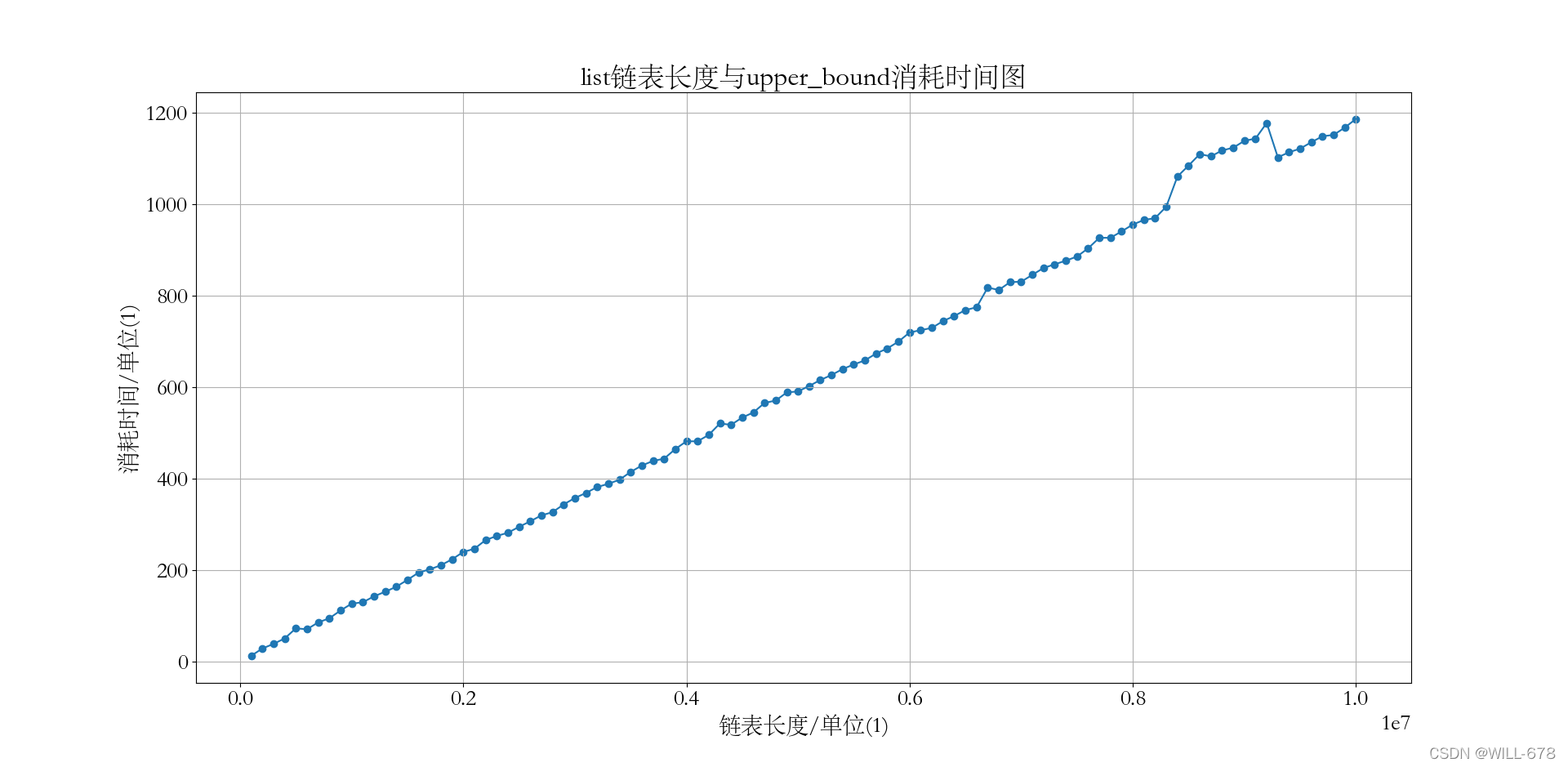
发现时间复杂度确为 O ( n ) \mathcal{O}(n) O(n)