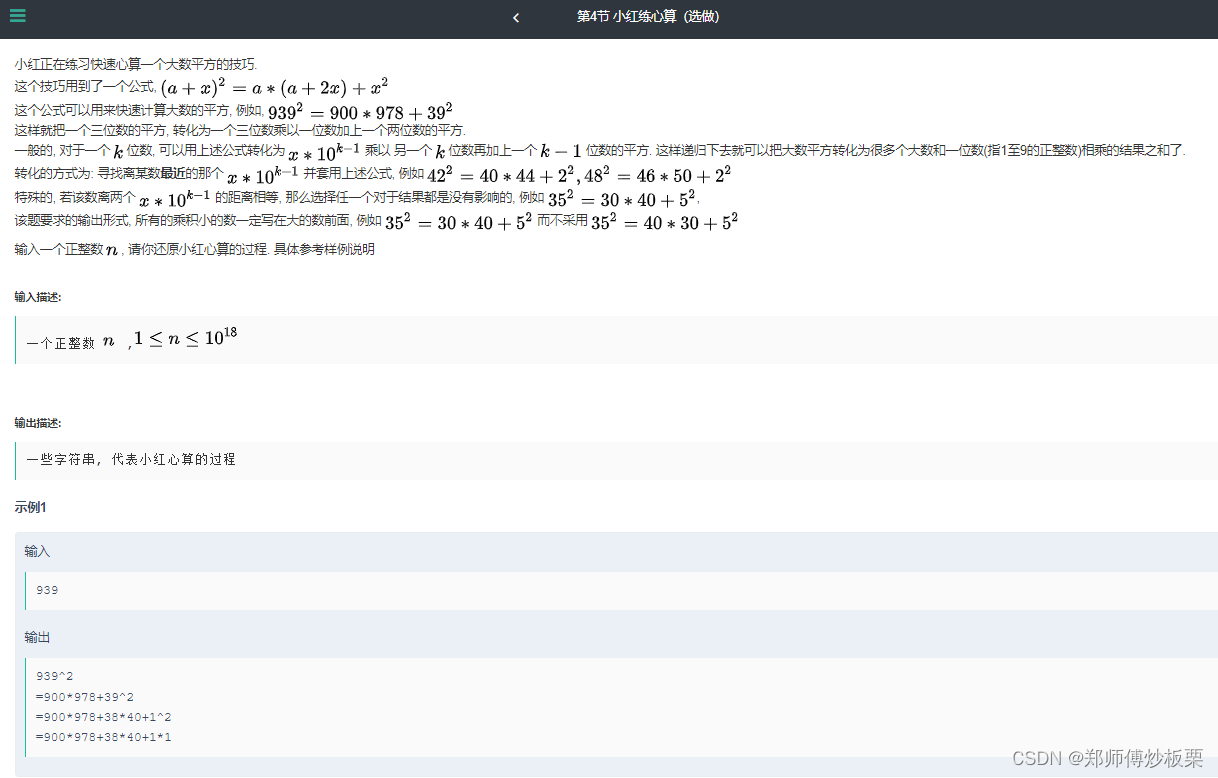
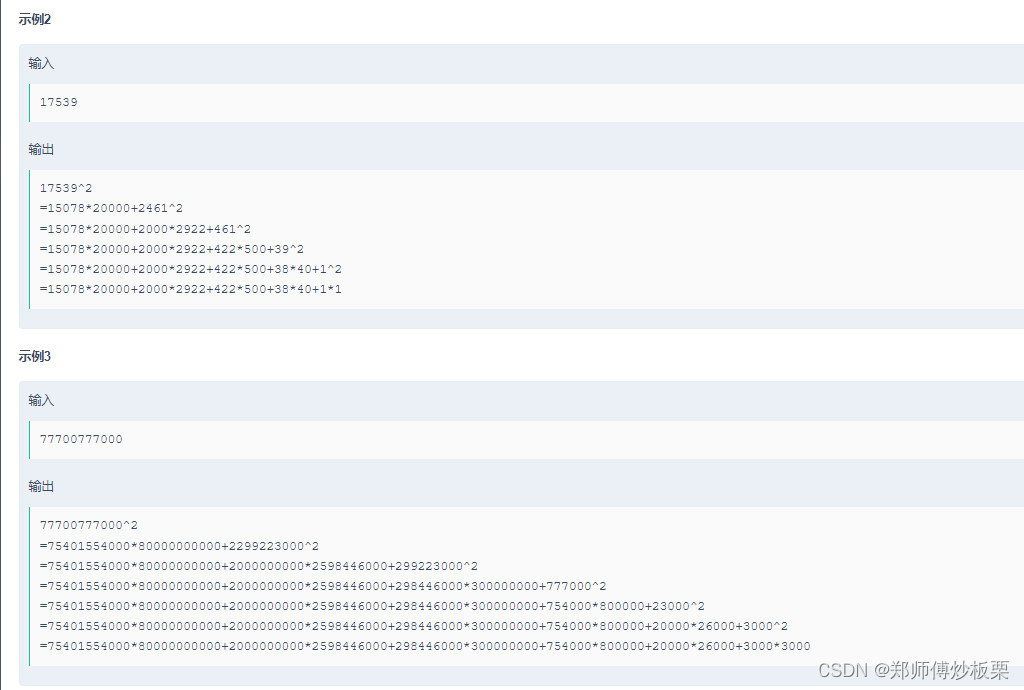
- 思路:把握三个数字,构造一个函数,返回值是下一个平方的数字(m),然后更新a(k:全局变量)与a+2*x(t:全局变量,!!!但是但是,为了最后的输出方便,t就接收较大的值,也就是说t可等于更新后的a,例如:48 ,k = 46,,t = 50,看代码吧,这里说的不好),这里我们用括号里面的数字简略代替,什么意思呢?我们用939来举例
- 经过一次函数调用之后,k = 900,t = 978,m = 39(待平方的数字);
- 所有的乘积小的数一定写在大的数前面
- 这题用long long,数据挺大的;
- 可以算一下,n - k = t - n
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll k, t, n; // 三个数字
//求出下一个要平方的数字,并且更新k,t
ll getPF(ll n) {
// 先求出n靠哪两个数
// 再比较靠这两个数,哪个更近
ll cnt = 0;
ll p1 = n;
// 例如:
// 939 -> 93 cnt = 1 -> 9 cnt = 2 2个0
// 900 (9 + 1)00 = 1000
while (p1 >=10) {
p1 /= 10;
cnt++; // 计次++
}
ll p2 = p1 + 1;
while (cnt--) {
p1 *= 10;
p2 *= 10;
}
// 按照与两个数字的差距来判断距离哪个更近
if (n - p1 > p2 - n) { // n距离p2更近 ,而p2是较大的数,由t接收
t = p2;
k = 2 * n - t; // n - k = t - n; 例如:939 939 - 900 = 978 - 939 所谓的2x
return p2 - n;
}
else {
k = p1;
t = 2 * n - k;
return n - p1;
}
}
string intToString(ll g) { // 将整数转换为字符串
string res = "";
while (g){
res = char (g % 10 + '0') + res;
g /= 10;
}
return res;
}
// 这个模拟就很复杂了,但是没有任何的算法
int main () {
// 若下一个要平方的n为0,+就不用写了,并且程序退出
cin >> n;
string tmp = "=";
while (n > 0) {
cout << n << "^2" << endl; // 输出遇到^2就换行
n = getPF(n);// 得到下一个要平方的n
tmp += intToString(k) + "*" + intToString(t);
// 若 n 不为0,则要加上“+”,等下还要计算
if (n) tmp += "+";
cout << tmp;
}
return 0;
}
