数位DP是一种特殊的计数DP, 与数字统计有关,一般求满足限制条件的第K小的数是多少,或者求在区间[L, R]内有多少满足条件的数字.
解决方法:
法一 :先用动态规划预处理出辅助数组,基于"拼凑"思想,用"试填法"求出最终的答案.
法二 :使用记忆化搜索实现
无论是从思维难易度, 还是从代码实现来说, 都是法二比较简单.所以个人推荐法二.
(动态规划预处理部分的作用充当记忆作用,事实上这就是动态规划的本质)
例题一:

直接从前向后枚举答案的每一位数(从小到大枚举)是多少,计算在这样的前缀下,后面的总排列数,如果加起来大于等于C, 说明当前的一位数就是这个枚举的数,我们继续讨论下一位即可.
我们先用动态规划预处理出木板的方案数.记为当前有i块不相同的木板,第一块木板的长度是排名第j(注意不是长度为j,这里指的是相对顺序,运用了离散化思想,等价转化了子问题),并且位状态(0表示低位,1表示高位)为k的木板序列的总方案数.
.
接下来试填即可.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 25;
int f[N][N][2];
void prework(){
f[1][1][0] = f[1][1][1] = 1;
for (int i = 2; i <= 20; ++i)
for (int j = 1; j <= i; ++j){
for (int p = j; p <= i - 1; ++p)
f[i][j][0] += f[i - 1][p][1];
for (int p = 1; p <= j - 1; ++p)
f[i][j][1] += f[i - 1][p][0];
}
}
void solve(){
int n, c;
cin >> n >> c;
bool used[N] = {0};
int last, k;//last表示前一位的高度,k表示前一位的状态
//因为第一位无法确定高位低位,所以我们独立处理第一位
for (int i = 1; i <= n; ++i){
//注意字典序是从小到大,应该先讨论当前位高位,再讨论当前位低位
if (f[n][i][1] >= c){
last = i, k = 1;
break;
} else
c -= f[n][i][1];
if (f[n][i][0] >= c){
last = i, k = 0;
break;
} else
c -= f[n][i][0];
}
used[last] = true;
cout << last << " ";
//枚举当前位是i位
for (int i = 2; i <= n; ++i){
k ^= 1;
//j表示长度的排名, len表示真实的长度,两者不一定相等
int j = 0;
for (int len = 1; len <= n; ++len){
if (used[len])
continue;
++j;
if ((k == 0 && len < last) || (k == 1 && len > last)){
if (f[n - i + 1][j][k] >= c){
last = len;
break;
} else
c -= f[n - i + 1][j][k];
}
}
used[last] = true;
cout << last << " ";
}
cout << "\n";
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
prework();
int T;
cin >> T;
while (T--)
solve();
}例题二: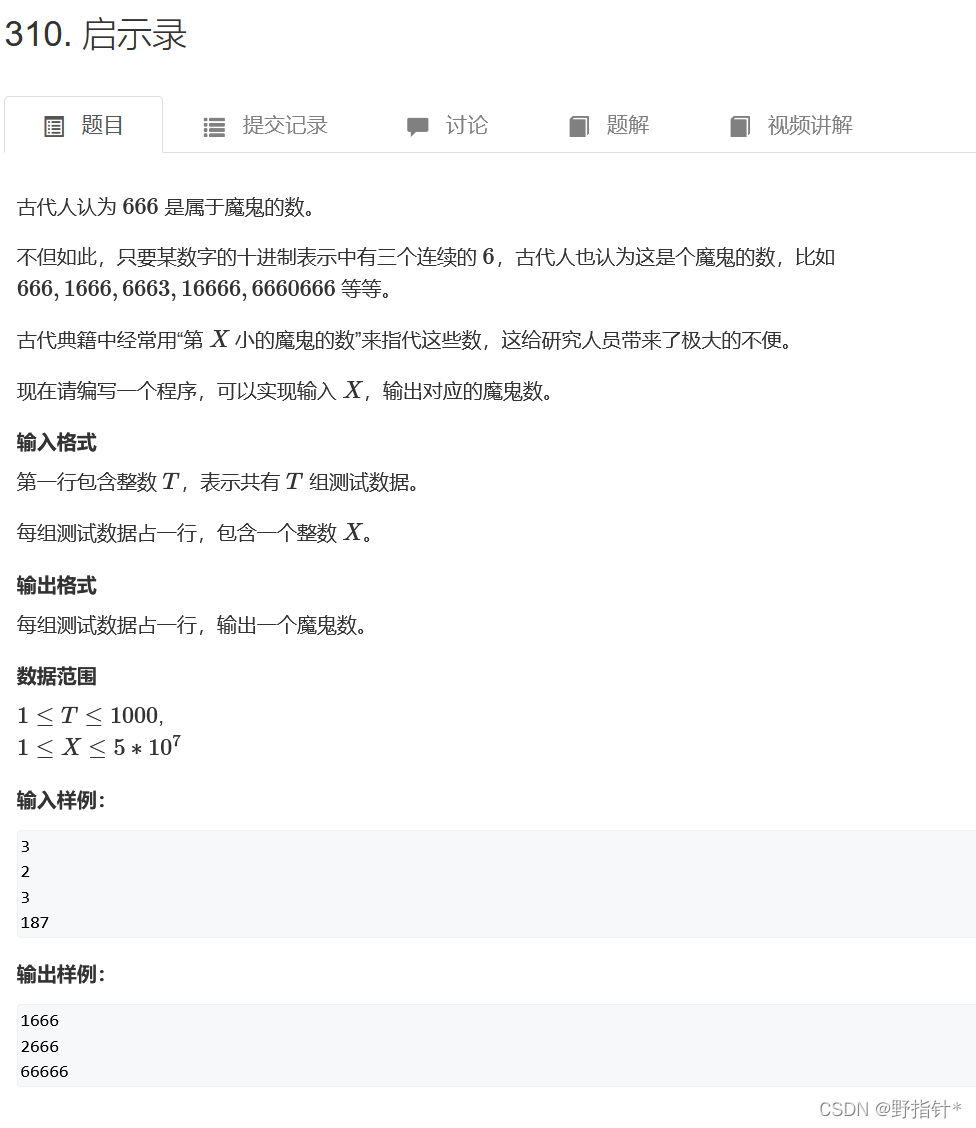
?法一 (动态规划预处理):我们依然使用试填法来解决这道题.我们先求出第X小的魔鬼数的位数,再从高位到低位(从左到右)从小到大枚举每一位可以填什么数字.
首先,我们用动态规划预处理出一个辅助数组和
,前者表示有i位,且从最高位开始数起,有连续(0 / 1 / 2)个6的方案数,注意!这个方案数是包含前导0的!后者则表示i位数字下有多少数字是有连续的666存在的(注意不一定是魔鬼数, 因为魔鬼数没有前导0)
有:
//我们以最高位(第i位)填什么数字作为依据来划分状态
f[i][0] = 9 * (f[i - 1][0] + f[i - 1][1] + f[i - 1][2]);//最高位除了6以外都可以填,除了最高位以外,最前面可以不填6,填1个6,也可以填2个6,至于为什么不把填更多6的情况算上,我们待会会解释
f[i][1] = f[i][0];//最高位填6,下一位一定不填6
f[i][2] = f[i][1];//最高位填6,下一位一定只能填1个6
c[i] = 10 * c[i - 1] + f[i - 1][2];
在这里,f数组只起到一个辅助g数组递推的作用(并且只有f[i - 1][2]起作用),所以我们只用求出f[i - 1][2]即可,要求出f[i - 1][2]只需要f[i - 1][0]和f[i - 1][1]即可,并且还要限制连续的6的长度小于等于2.
接下来我们使用试填法,首先,我们先找出魔鬼数是多少位,假设m为位数,m >= 3,我们从m = 3开始枚举,直到c[m] >= X, 注意不是拿前缀和去枚举,因为c[i]不是魔鬼数的方案数,而是包含666的数字的方案数.接下来我们枚举每一位填什么即可.具体情况见注释:
#include <bits/stdc++.h>
#define int long long
using namespace std;
int f[30][5], c[30];
void prework(){
f[0][0] = 1;
c[0] = 0;
for (int i = 1; i <= 20; ++i){
f[i][0] = 9 * (f[i - 1][0] + f[i - 1][1] + f[i - 1][2]);
f[i][1] = f[i - 1][0];
f[i][2] = f[i - 1][1];
c[i] = 10 * c[i - 1] + f[i - 1][2];
}
}
void solve(){
int X;
cin >> X;
int m;
for (m = 3; c[m] < X; ++m);
//i是当前枚举的位数,(当前一轮未更新的)k表示当前从第i - 1位数起有连续的k个6, 当k >= 3时,这个数就已经是魔鬼数了, 我们取k = 3时魔鬼数个数 + 1.
for (int i = m, k = 0; i; --i){
//枚举当前的位可以填什么数
for (int j = 0; j <= 9; ++j){
//cnt表示后面剩余的数字可以组成的包含666的数的个数
int cnt = c[i - 1];
//我们当前一共有(k + (j == 6)接下来我们只需要再找(3 - (k + (j == 6)) 个数就能拼凑成魔鬼数了
//或者当前前面已经有3个6了,一定是魔鬼数
if (j == 6 || k == 3)
for (int l = max(3 - (k + (j == 6)), 0ll); l < 3; ++l)
cnt += f[i - 1][l];
if (cnt >= X){
cout << j;
if (k < 3){
if (j == 6)
++k;
else
k = 0;
}
break;
}
else
X -= cnt;
}
}
cout << "\n";
}
signed main(){
prework();
int T;
cin >> T;
while (T--)
solve();
}法二(记忆化搜索) : 本质依然是试填法,从最高位填起,我们假设f[pos][now][ok]表示当前的位置为pos,已经有连续的now个6,且当前的数是/否(ok == true)魔鬼数(并且没有最高位和前导0的限制).
接下来开始填数,我们举个例子,3214666, 当第一位填的是3, 那么第二位最多只能填2, 如果第一位不是3, 那么第二位最多可以填9, 以此类推, 每一位最多能填多少取决于前一位是否达到了极限,我们可以用lim记录状态,zero则表示前面是否为前导0.
代码实现如下:
?
#include <bits/stdc++.h>
#define int long long
using namespace std;
int l, r;
int f[12][100][100];
int a[12];
int res;
int dfs(int pos, int sum, int mod, bool lim, bool zero) {
if (pos == 0)
return sum == res && mod == 0;
if (!lim && !zero && f[pos][sum][mod] != -1)
return f[pos][sum][mod];
int ans = 0;
int maxx = lim ? a[pos] : 9;
for (int i = 0; i <= maxx; ++i)
ans += lim && i == maxx ? dfs(pos - 1, sum + i, (mod * 10 + i) % res, 1, 0) :
dfs(pos - 1, sum + i, (mod * 10 + i) % res, 0, zero && i == 0);
return lim || zero ? ans : f[pos][sum][mod] = ans;
}
int solve(int x) {
if (x == 0)
return 0;
int ans = 0, len = 0;
do {
a[++len] = x % 10;
x /= 10;
} while(x);
for (res = 1; res <= 82; ++res) {
memset(f, -1, sizeof f);
ans += dfs(len, 0, 0, 1, 1);
}
return ans;
}
signed main() {
while (cin >> l >> r)
cout << solve(r) - solve(l - 1) << "\n";
}总结:
1.要求序列选连续最多不超过k个数(假设为k)的dp计数:
//f[i][j]表示当前考虑了i个数,从当前的序列结尾开始数起,一共连续选了j个数
f[i][0] = f[i - 1][0] + f[i - 1][1] + ... + f[i - 1][k];//当前不选,上一个数可以选0,1,2...k个数,因为不会选择超过k个数,所以只用计数这些情况即可
f[i][1] = f[i][0];//最后一位一定是选了,前面一位一定是没选
f[i][2] = f[i][1];//最后一位一定是选了,前面一位一定只选了一位
//...
f[i][k] = f[i][k - 1];//最后一位一定是选了,前面一位一定只选了k - 1位
2.要求序列多次选择中至少有一次连续选k个数的dp计数
首先,我们预处理出f[i][k - 1]表示当前考虑了i个数,从当前的序列结尾开始数起,一共连续选了k - 1个数, 接下来,c[i]表示序列长度位i满足题意的方案数:
,其中num表示当前一位能选的数的方案数.
例题三:
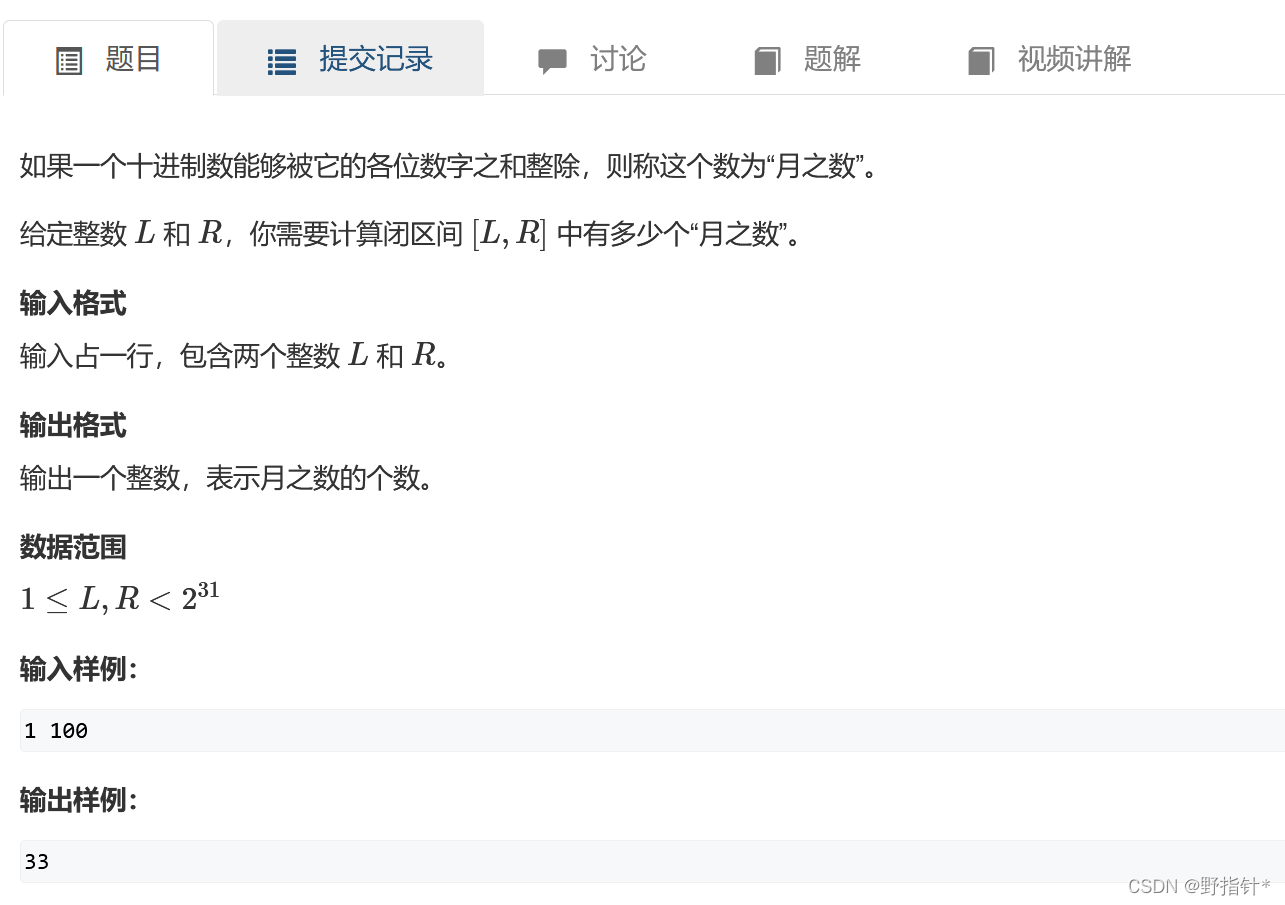
这道题我只给出第二种做法,(因为第一种我看不懂hh).
#include <bits/stdc++.h>
#define int long long
using namespace std;
int l, r;
int f[12][100][100];//f[pos][sum][mod]表示当前的位数位pos, 总和为sum, 模上res为mod的所有的方案数(没有最高位和前导0的限制)
int a[12];
int res;
//pos表示当前讨论的位数(1~k位), sum表示已填的数字的和,mod表示已填数字的和对res的取模, lim表示前一位是否到达可选的极限,zero表示前一位是否前导0
int dfs(int pos, int sum, int mod, bool lim, bool zero) {
if (pos == 0)
return sum == res && mod == 0;
//如果前一位是前导0或者已经到达可选的极限,那么不能直接返回,因为当前有限制,而f[pos][sum][mod]是没有限制的
if (!lim && !zero && f[pos][sum][mod] != -1)
return f[pos][sum][mod];
int ans = 0;
//如果当前是最高位,那么最高位应该选a[pos]
int maxx = lim ? a[pos] : 9;
for (int i = 0; i <= maxx; ++i)
ans += lim && i == maxx ? dfs(pos - 1, sum + i, (mod * 10 + i) % res, 1, 0) :
dfs(pos - 1, sum + i, (mod * 10 + i) % res, 0, zero && i == 0);
//如果当前有限制,也不能对f[pos][sum][mod]赋值
return lim || zero ? ans : f[pos][sum][mod] = ans;
}
int solve(int x) {
if (x == 0)
return 0;
int ans = 0, len = 0;
do {
a[++len] = x % 10;
x /= 10;
} while(x);
//枚举所有位数的总和,求方案数
for (res = 1; res <= 82; ++res) {
memset(f, -1, sizeof f);
ans += dfs(len, 0, 0, 1, 1);
}
return ans;
}
signed main() {
while (cin >> l >> r)
cout << solve(r) - solve(l - 1) << "\n";
}例题四:
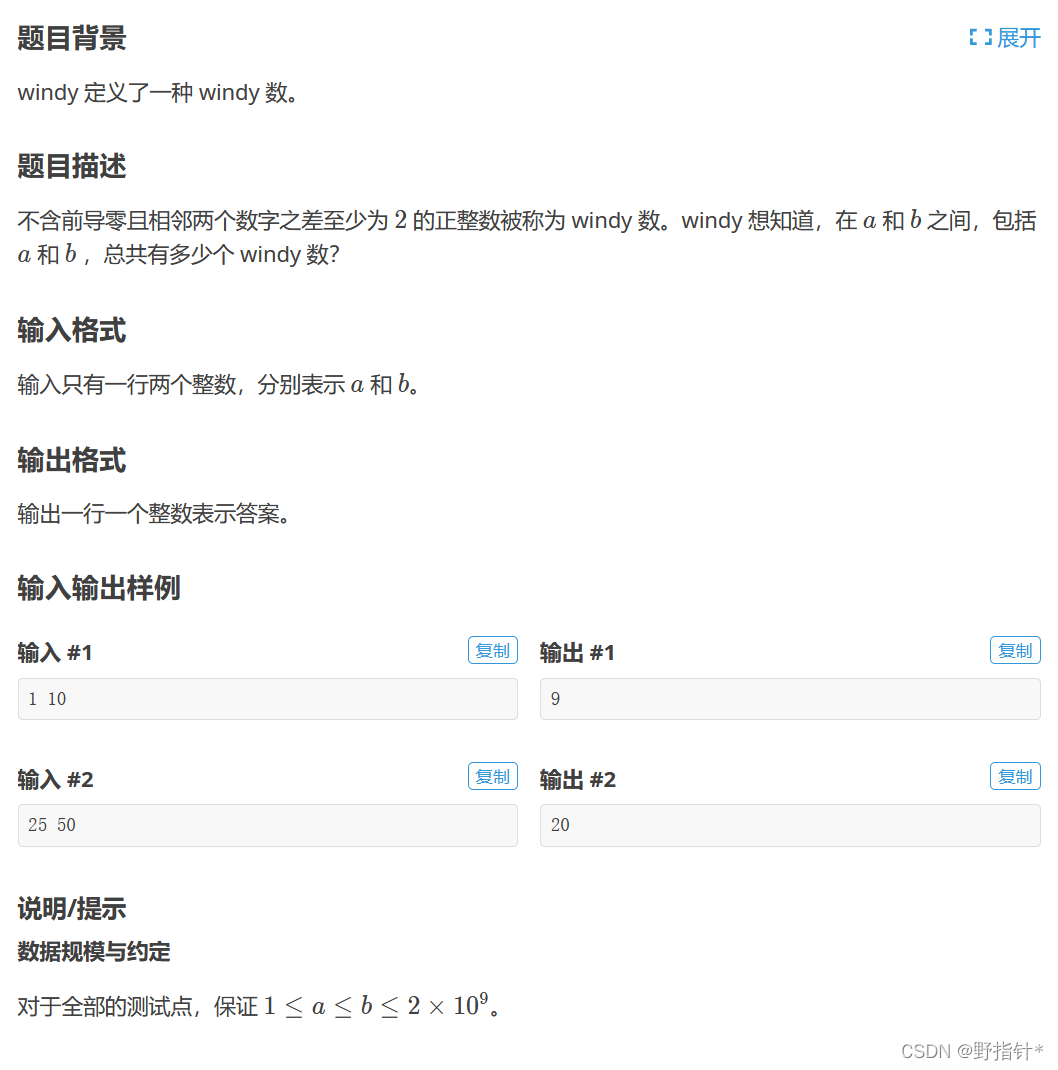
#include <bits/stdc++.h>
#define int long long
using namespace std;
int l, r;
int f[12][100][100];
int a[12];
int res;
int dfs(int pos, int sum, int mod, bool lim, bool zero) {
if (pos == 0)
return sum == res && mod == 0;
if (!lim && !zero && f[pos][sum][mod] != -1)
return f[pos][sum][mod];
int ans = 0;
int maxx = lim ? a[pos] : 9;
for (int i = 0; i <= maxx; ++i)
ans += dfs(pos - 1, sum + i, (mod * 10 + i) % res, lim && i == maxx, zero && i == 0);
return lim || zero ? ans : f[pos][sum][mod] = ans;
}
int solve(int x) {
if (x == 0)
return 0;
int ans = 0, len = 0;
do {
a[++len] = x % 10;
x /= 10;
} while(x);
for (res = 1; res <= 82; ++res) {
memset(f, -1, sizeof f);
ans += dfs(len, 0, 0, 1, 1);
}
return ans;
}
signed main() {
while (cin >> l >> r)
cout << solve(r) - solve(l - 1) << "\n";
}例题五:

代码实现如下:
?
#include <bits/stdc++.h>
#define int long long
using namespace std;
int a[100];
int f[15][10000];
int dfs(int pos, int v, int sum, bool lim, bool zero) {
if (pos == 0)
return sum;
if (!lim && !zero && f[pos][sum] != -1)
return f[pos][sum];
int ans = 0, maxx = lim ? a[pos] : 9;
for (int i = 0; i <= maxx; ++i)
//在这里要特别注意,当计算0的个数时,当前一位不能是前导0
ans += dfs(pos - 1, v, sum + ((i == v) && !(zero && i == 0)), lim && i == maxx, zero && i == 0);
return lim || zero ? ans : f[pos][sum] = ans;
}
int query(int x, int val) {
int len = 0;
do {
a[++len] = x % 10;
x /= 10;
} while(x);
return dfs(len, val, 0, 1, 1);
}
signed main() {
int l, r;
while (cin >> l >> r, l || r) {
if (l > r)
swap(l, r);
//枚举0~9, 分别对每个数进行计数
for (int i = 0; i <= 9; ++i){
memset (f, -1, sizeof f);
cout << query(r, i) - query(l - 1, i) << " ";
}
cout << "\n";
}
}例题六:
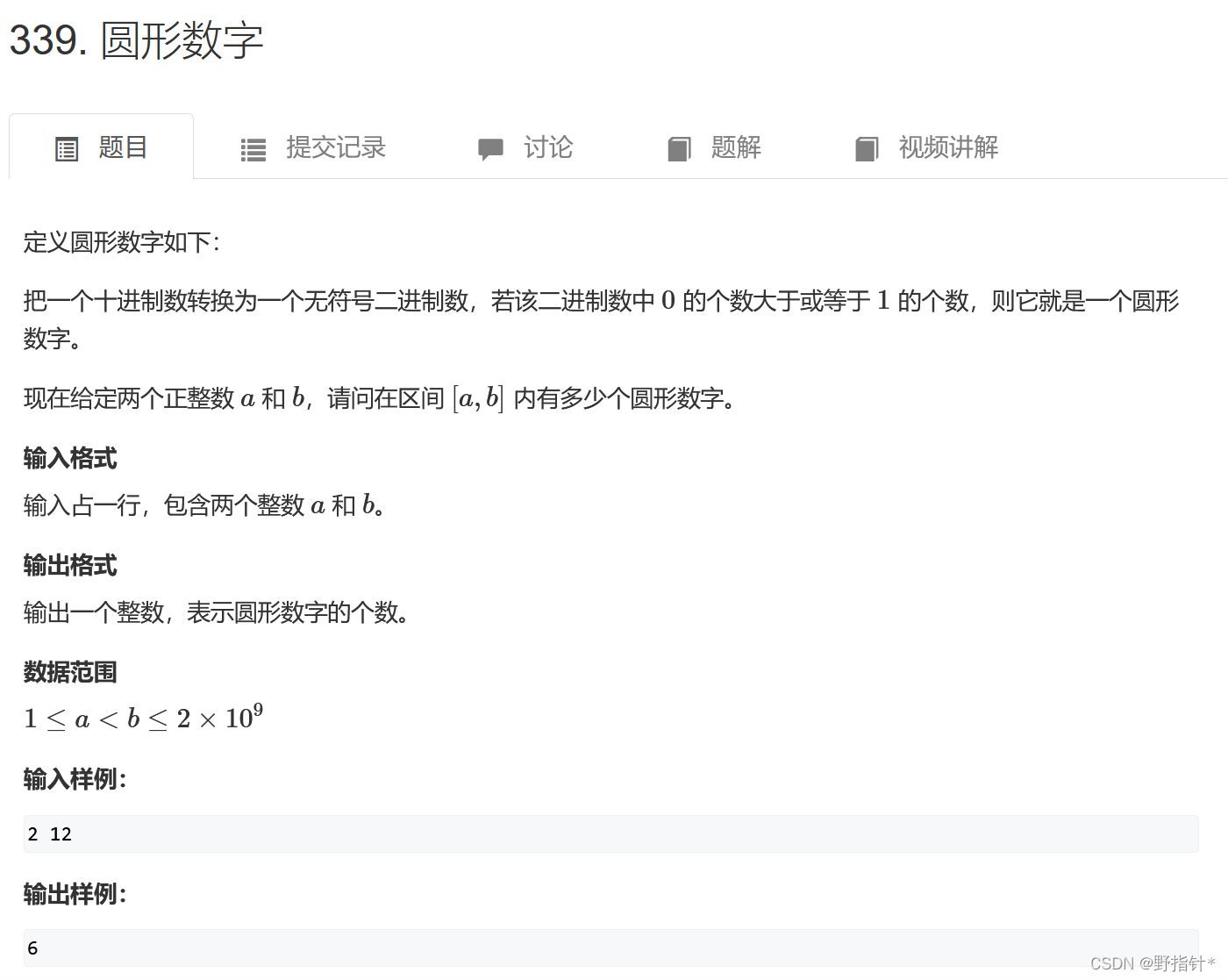
?
#include <bits/stdc++.h>
using namespace std;
int l, r;
int a[100], f[65][65][65];
int dfs(int pos, int cnt0, int cnt1, bool lim, bool zero) {
if (pos == 0)
return cnt0 >= cnt1;
if (!lim && !zero && f[pos][cnt0][cnt1] != -1)
return f[pos][cnt0][cnt1];
int ans = 0, maxx = lim ? a[pos] : 1;
for (int i = 0; i <= maxx; ++i)
ans += dfs(pos - 1, i == 1 ? cnt0 : cnt0 + 1 - zero, cnt1 + (i == 1), lim && i == maxx, zero && i == 0);
return lim || zero ? ans : f[pos][cnt0][cnt1] = ans;
}
int query(int x) {
int len = 0;
do {
a[++len] = x % 2;
x /= 2;
} while (x);
return dfs(len, 0, 0, 1, 1);
}
signed main() {
cin >> l >> r;
memset(f, -1, sizeof f);
cout << query(r) - query(l - 1) << "\n";
}