[C++知识库]从操作系统理解计算机—程序结构与存储（2）

本系列内容整体框架借鉴了 👉《深入理解计算机系统 第三版》👈 但是许多内容并不限于这本书，计算机操作系统的理解并不是一蹴而就的，往往需要结合实际项目深入理解。希望通过这部分专栏的内容能够让读者深入的了解并理解计算机组成以及计算机操作系统。
此外,博主觉得尽管计算机硬件的设计是计算机操作系统的根本，但是不妨换一个思路，从操作系统方向理解计算机😺从操作系统理解计算机😸，如果硬件的设计是为了软件更好的运行，这种设计是否可以实现系统更加高效运行，这个问题值得深思

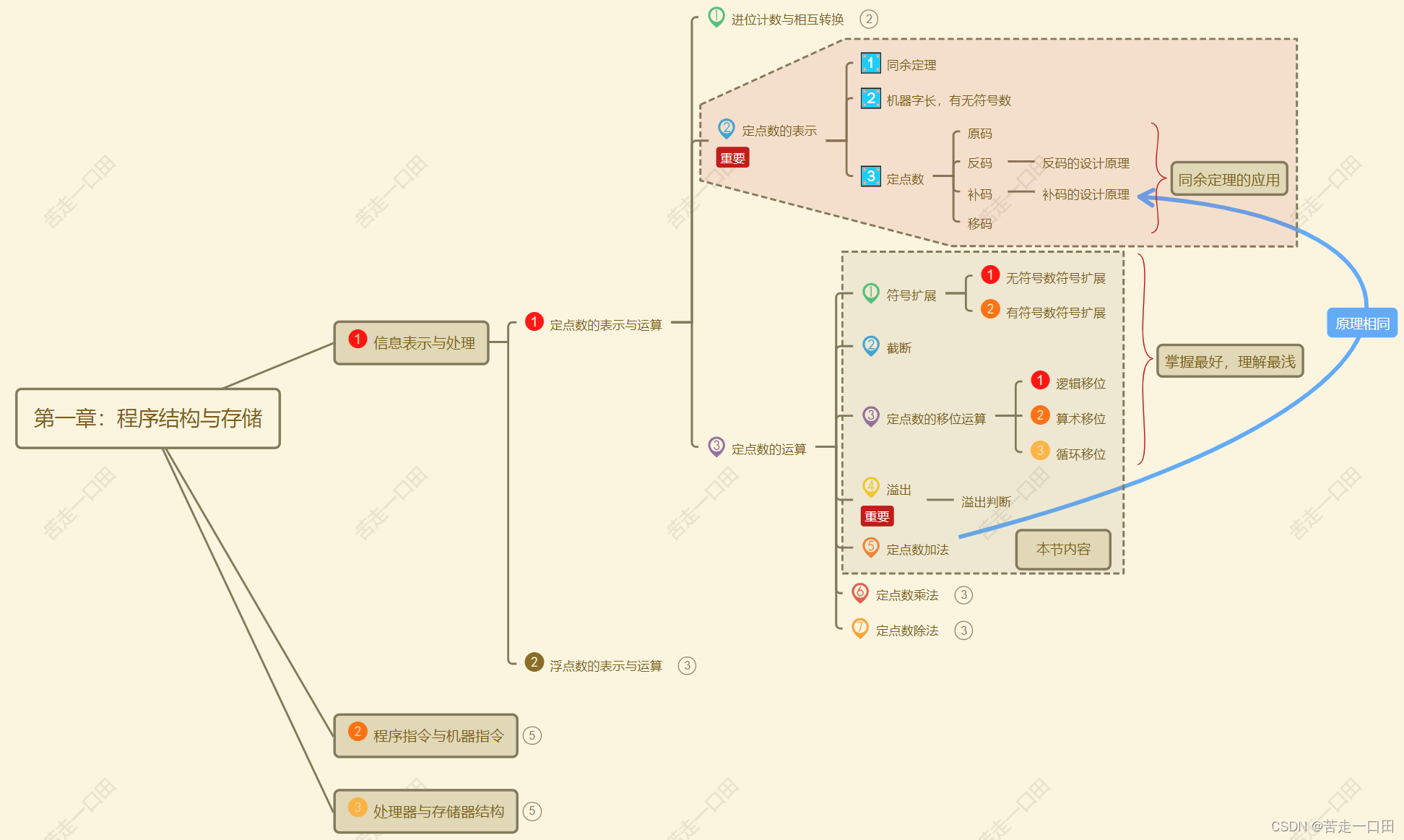
每章都配有思维导图哟,阅读上1万后期会出视频
首先上一段极为经典的代码：

#include <stdio.h>
int main()
{
	printf("Hello, World !\n");
	return 0;
}

这段程序就是计算机中所有程序的代表，狭义上学习操作系统就是来理解程序在执行过程中操作系统都干了什么。为了帮助读者更好的理解程序与操作系统之间的，这里引出一个我自创的定义(其实是借鉴产品生命周期管理)——PLM（程序生命周期管理 Program Lifecycle Management）

程序的一般运行过程如上图，理解一个程序与系统之间的关系，首先需要理解这些程序代码在系统中是如何存放的，为此引出本章内容——程序结构与存储

在上一节的内容中，我们研究了计算机整数的表示方法与设计原理，本文是乘法与除法运算的前置章节，本文的内容很杂但确是重要的基础内容。当然如果觉得本文的内容不好理解的话，也可以直接使用结论，后期的内容逐渐理解本文内容即可。

本节思维导图如下：

一、定点数的运算

1.1 符号扩展

计算机无时无刻不再进行着各种各样的运算，
一般的运算过程会需要在不同字长的整数之间进行转换一般情况下都是较短字长的数向较长字长的数的转化，这种情况大多数属于正常情况，至于长字长数据转换为短字长数据（这个过程称为截断），这个过程往往会发生各种各样的问题。这里首先讨论短字长整数转换长字长数据（这个过程也称为符号扩展）。

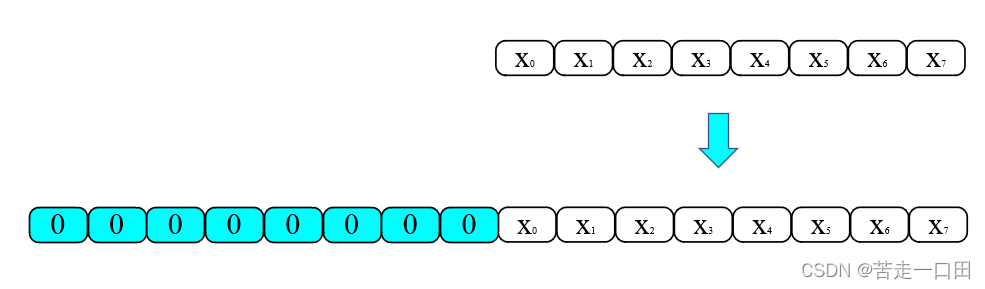
1.1.1 无符号数的符号扩展(0扩展)

无符号数的扩展仅仅需要在整数开头直接加“0”就可可以，例如一个8位无符号数向16位无符号数扩展,如下：

1.1.2 有符号数的符号扩展

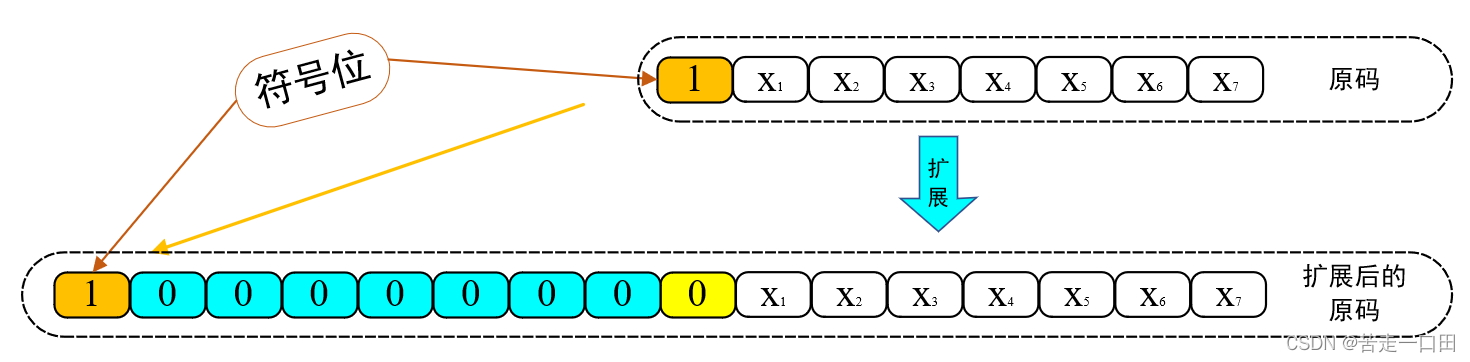
有符号数的符号扩展较为复杂，但是并不难。复杂的原因是在有符号数中需要讨论各种码制的符号扩展，对于正数，原码、反码和补码的符号扩展与无符号数相同，直接在开头添“0”即可。这里主要讨论负数的符号扩展。

1. 负数原码与反码的符号扩展

• 负数原码符号扩展
  负数原码的符号扩展与正数相同，只不过符号位为1，如下图
  

---

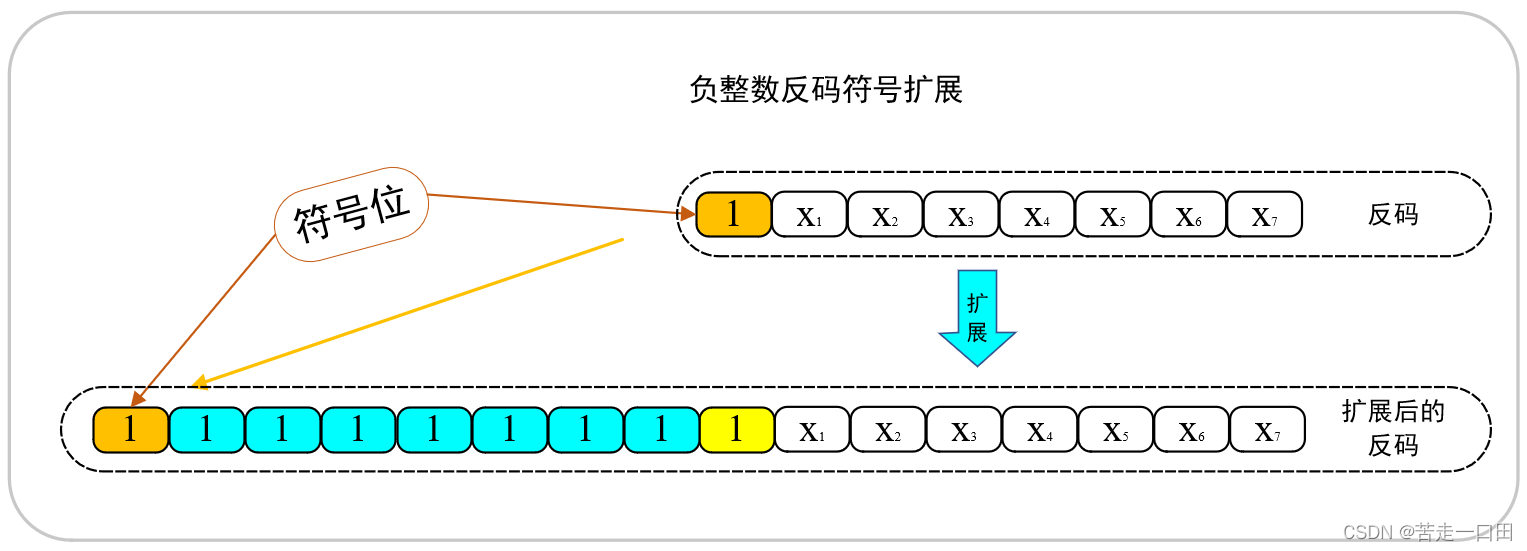
• 负数反码符号扩展
  这里可以回忆一下上一节的内容——从操作系统理解计算机—程序结构与存储（1）
  以负整数反码为例：
  $$x_{反码}=x_{真值}mod(2^n?1)=\{\begin{array}{l}0,x{2}^{n?1}>x\ge 0\\ 2^n?1+x0\ge x>?2^{n?1}\end{array}$$
  
  从8位扩展到16位过程其实就是从$2^8?1+x$到$2^{16}?1+x$的扩展过程。具体到数值的表现如下：
  
  反码的符号扩展可以称为“1扩展”，相当于在附加位上直接添“1”。
  负小数的符号扩展与整数相差不多，不过是在小数的尾部添“1”
  8位小数扩展为16位如下：

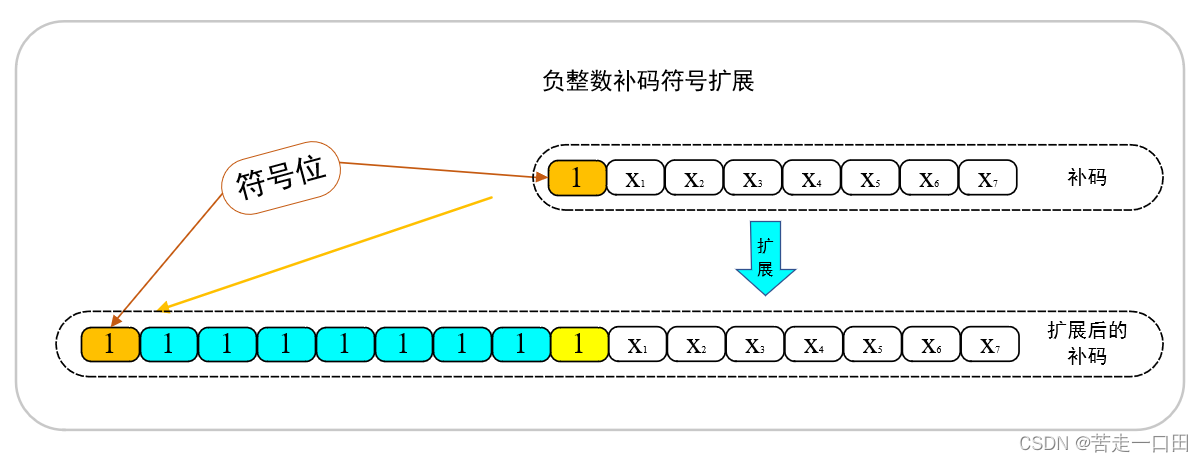
2. 负数补码的符号扩展

这里还是先回忆上一节我们讲的补码的函数定义——从操作系统理解计算机—程序结构与存储（1）

• 负数补码整数
  
  $$x_{补码}=x_{真值}mod(2^n)=\{\begin{array}{l}0,x{2}^n>x\ge 0\\ 2^n+x=2^n?|x|0>x\ge ?2^{n?1}\end{array}$$
  
  
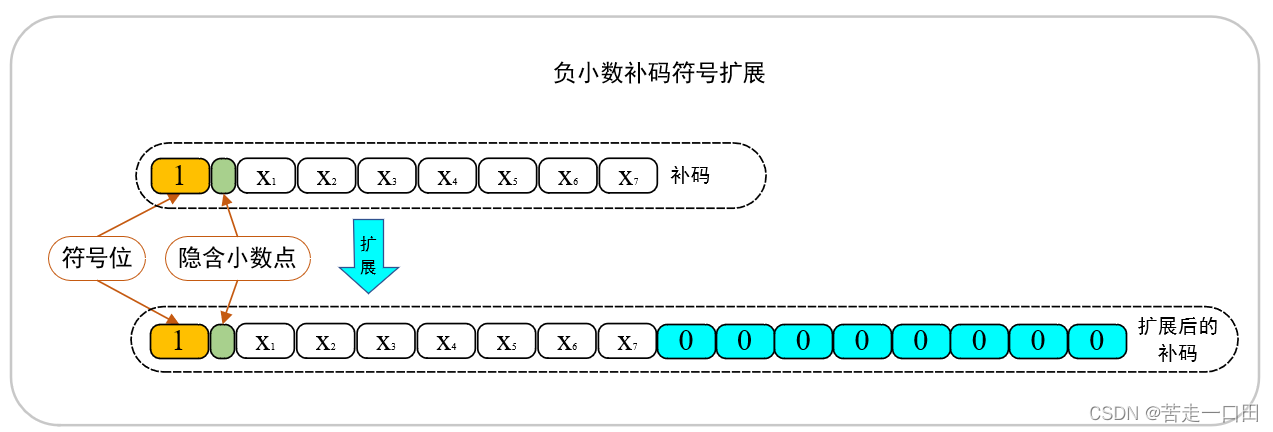
• 负数补码小数
  
  $$x_{补码}=x_{真值}mod2=\{\begin{array}{l}x,1>x\ge 0\\ 2+x=2?|x|,0>x\ge ?1\end{array}$$
  
  依据定义，负数补码的符号扩展其实很简单，对负整数而言，补码的符号扩展就是$2^{N_0}+x$向$2^{N_1}+x$扩展的过程（$N_0<N_1$），以8位向16位扩展为例，负整数补码的符号扩展数值表现如下：
  
  负小数的补码与负整数补码不同,补码小数的定义是固定的——$2+x$，所以负小数补码的符号扩展直接在小数的尾部直接补“0”即可，以8位向16位扩展为例，负小数补码的符号扩展数值表现如下：
  

1.1.3 总结

1.2、 截断

以上内容介绍了符号扩展——其实就是短字长数向长字长数的转换，既然有扩展，那么就有长字长数向短字长数的转换，这种情况就是——截断。
截断过程其实很简单，无论任何数，截断的处理就是舍弃高位只留下低位。
截断不当会出现各种各样的问题，例如有符号数截断后的数依旧是有符号数，一个16位的有符号数0000 0000 1001 1111（补码）截断为8位>截断后的的数就变成了1001 1111（补码）显然正数变成了负数。这种错误在输出或者条件判断中都如意造成重大事故。
但是也不可以将截断直接视作故障，截断处理很多时候并不是一无是处。
例如，嵌入式系统中可以使用截断的方式直接将不常用的长字长数变短，进一步节省内存，当然在某些精简指令集的嵌入式系统中也可使用这种方式代替取余运算。

1.3 定点数的移位运算

移位操作是计算机重要的运算过程之一，移位操作主要有三种操作——逻辑移位、算术移位和循环移位。

1.3.1 逻辑移位

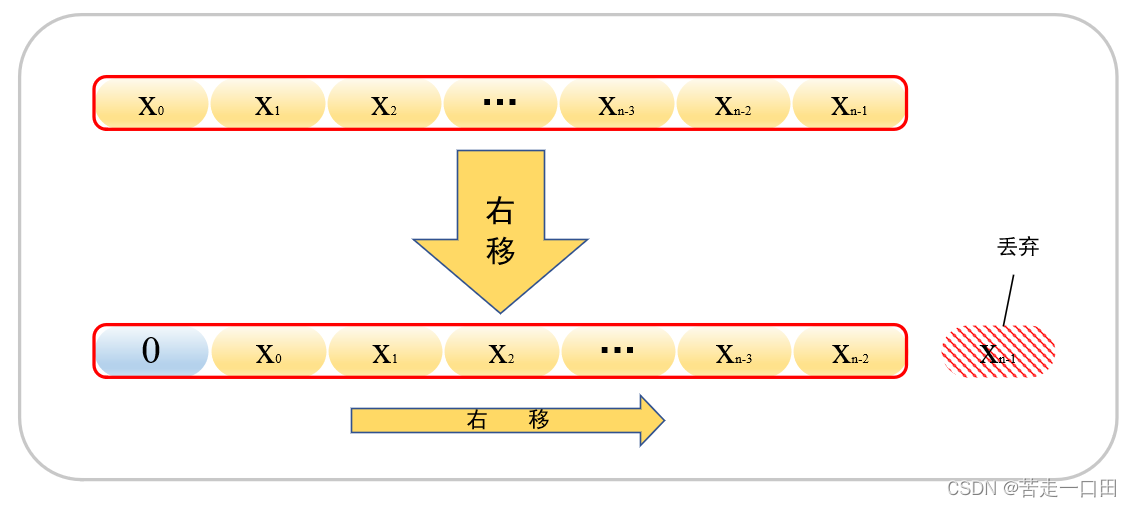
逻辑移位是基于位运算的基础上的，逻辑移位并不关心整体数值的大小，而是将着重点放在具体的位运算上。逻辑移位运算很简单——
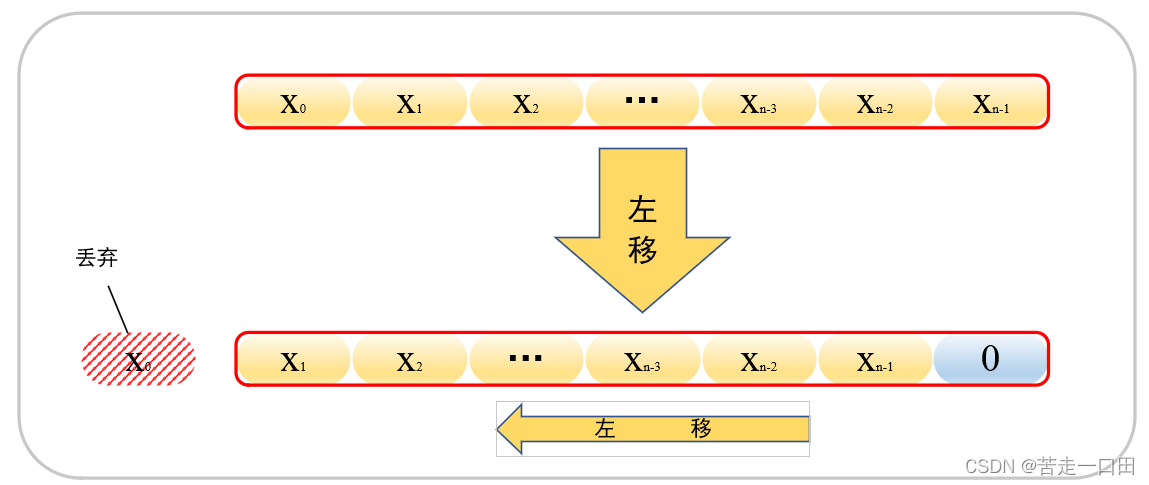
逻辑右移，丢弃低位，高位补0；逻辑左移,丢弃高位，低位补0。
逻辑右移操作过程如下：

逻辑左移操作过程如下：

1.3.2 算术移位

相较于逻辑移位，算术移位运算就比较难了，因为算术运算的对象主要是有符号数，移位过程需要保证有符号数的原有性质不变，所以算术移位的规则需要根据码制的不同改变算术移位规则。
算术移位操作是在数值基础上进行的移位操作，相较于逻辑移位，算术移位更加关注整体的数值的大小，所以算术移位不会改变符号位。

• 对于正数
  正数的原码、反码和补码都相同，所以算术移位规则也相同，无论算术左移还是算术右移都和逻辑移位相同。
• 对于负数：
  负数原码算术移位：负数原码的算术移位规则是符号位不变，数值位按逻辑移位操作
  负数反码算术移位：反码的算术移位是在原码的基础上进行的，所以负数反码的移位操作其实就是负数原码操作的转换——负数反码算术移位无论左移还是右移空出的位直接添1。
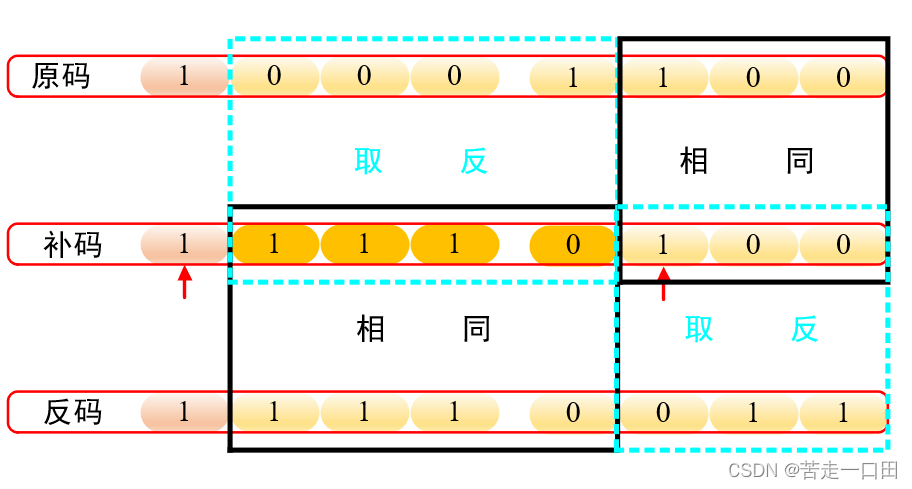
  负数补码算术移位：这里给出一个关于补码形式的重要推论——自补码最后为1的位起(不含这一位)，到符号位为止（不含符号位）的所有位全部取反，得到的便是负数的原码
  例如：数值 -12
  
  可以发现原码和反码关于补码中心对称的,补码的低位部分与原码相同,补码的高位部分与反码相同,所以补码的算术移位左移与原码相同--------添"0",右移与反码相同--------添"1"

算术移位总结

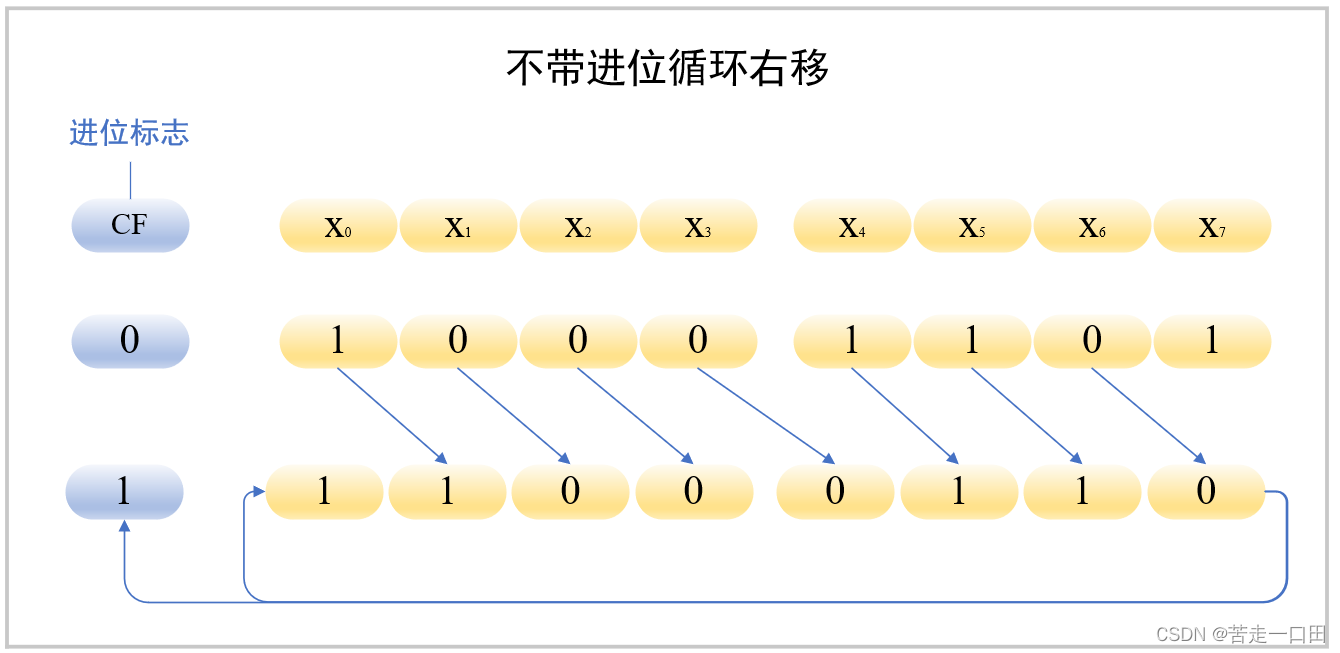
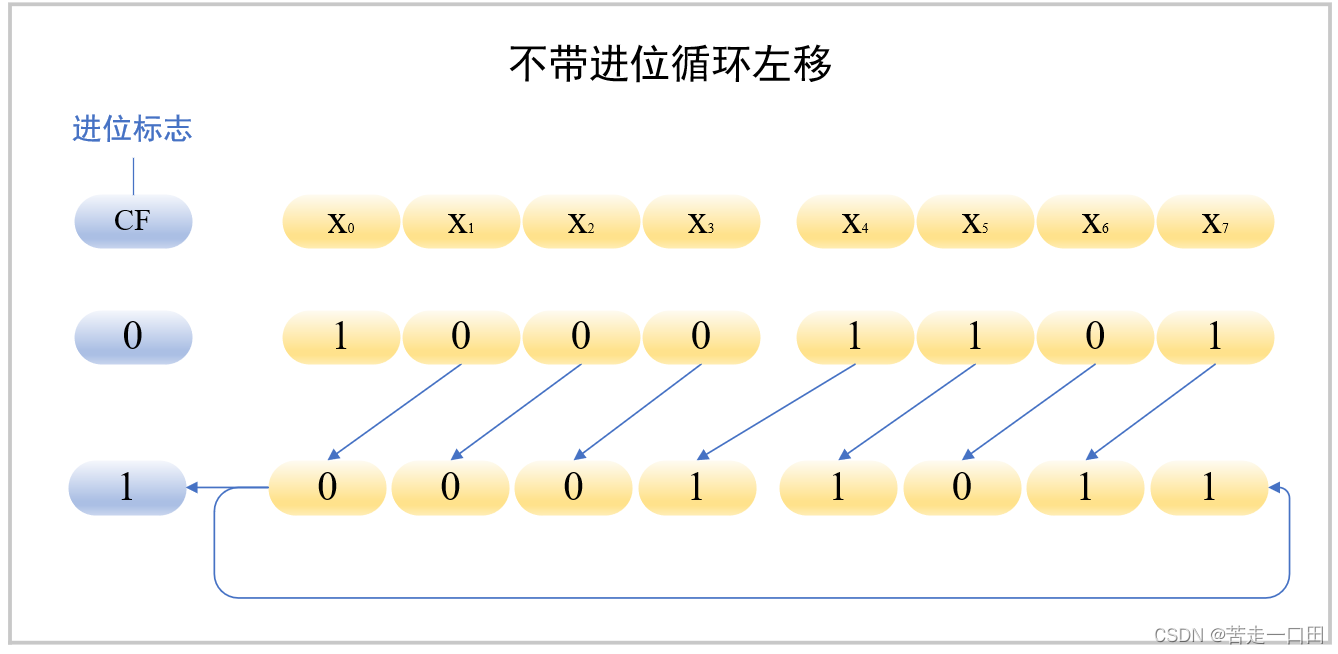
1.3.3 循环移位

循环移位具体有两种，带进位的循环移位和不带进位的循环移位。计算机最高位进位有专门的寄存器——CF,无论是带进位还是不带进位的循环移位都需要考虑进位寄存器。
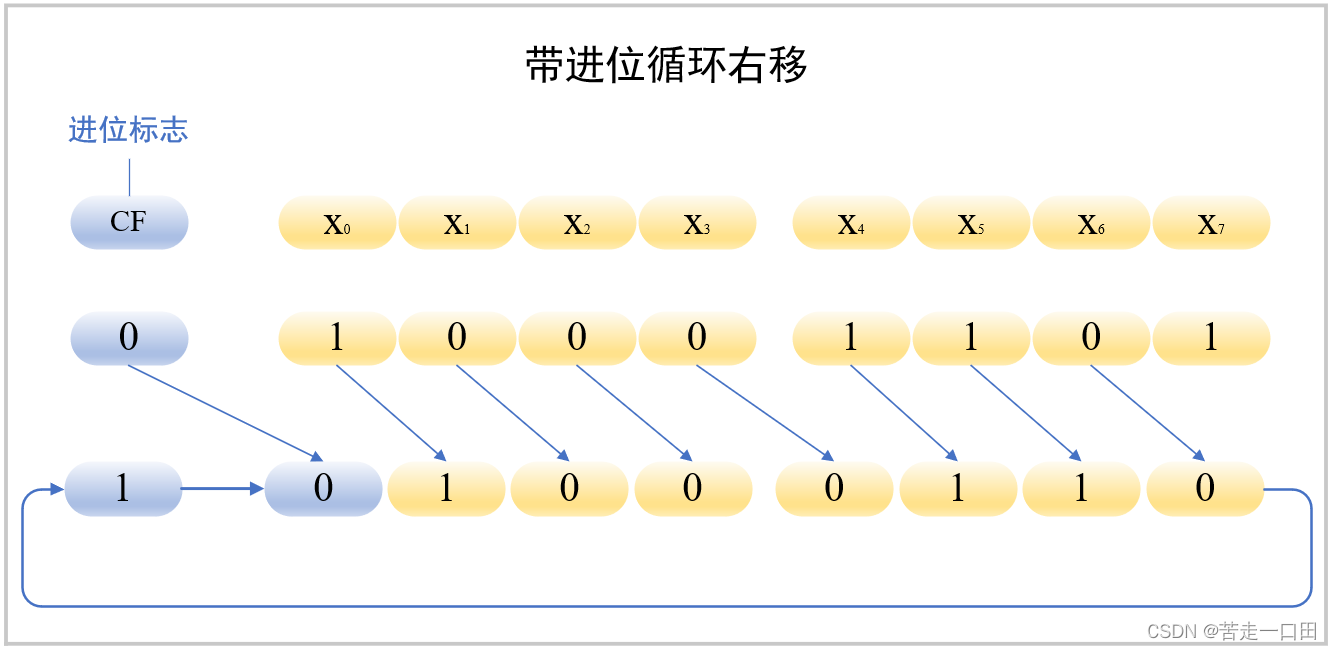
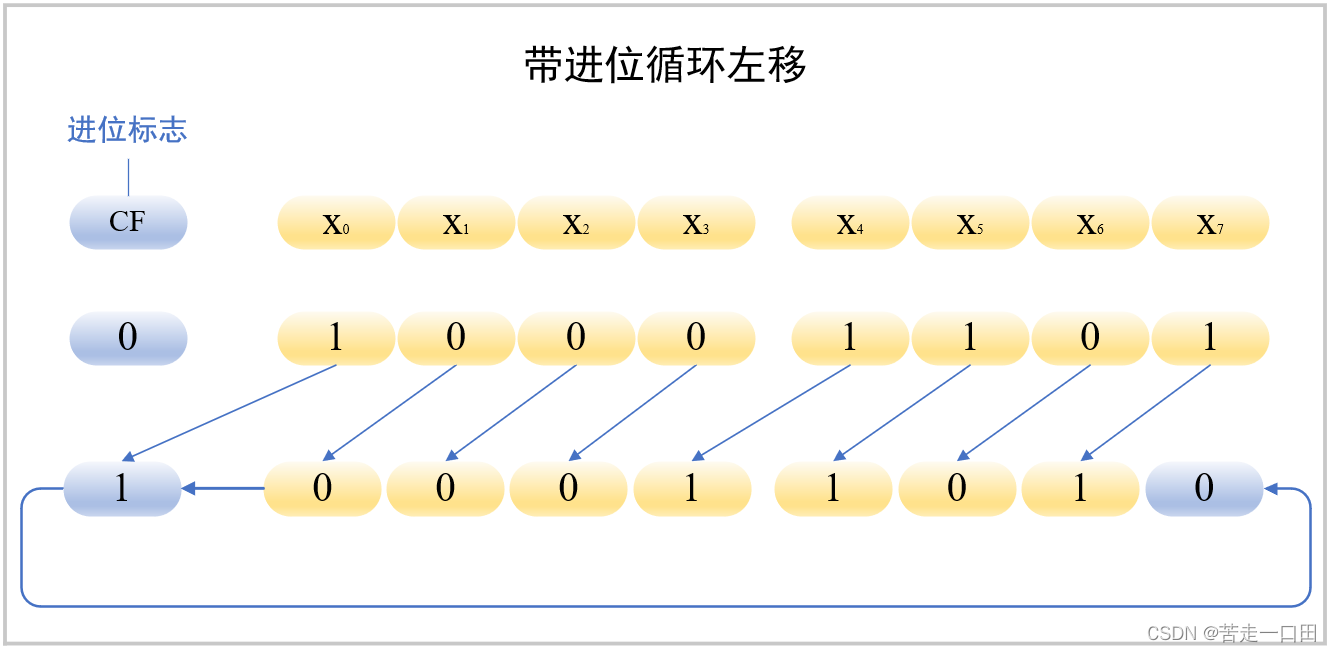
<font color=>带进位的移位就是将进位标志和数值看作一个整体，然后进行循环移位操作，以8位为例，循环右移和循环左移操作如下图：

不带进位的循环移位，右移时移出的一位需要在循环移位的基础上并且移出到CF寄存器，左移时同理，也是以8位为例，不带进位的循环移位具体操作如下：

1.4 溢出

在上一章讲解反码原理时提到一个概念——溢出。同时在讲解具体的算术运算时首先需要着重理解的内容就是溢出的概念。溢出其实很好理解——计算机能够表示的数的范围是有限的，当超过这个计算机能够表示的范围时就发生了溢出。

1.4.1 溢出的判断

既然了解的溢出的概念，那么如何判断溢出呢？

• 可以使用定义，这种方法适用于我们做题中常用
  例如，对无符号数而言(n位机器字长)
  $$x_1+x_2=y(0\le y<2^n)$$
  当发生溢出时，意味着计算结果$y\ge 2^n$。

现在的计算机绝大部分计算机系统都是以补码为基础的，为此我们主要研究计算机系统中补码溢出的判断方式。
这里给出有符号补码的三种判断溢出的方法：

---

1.采用一位符号位
对于有符号数而言，溢出的情况只有两种——正数加正数超限和负数加负数超限。
那么正数加正数超限的情况会发生什么，以n位机器字长为例，补码的最大的正数是$2^{n?1}?1$,也就是$0(符号位)1111\dots 1111（n?1个1）$当超过这个值以后意味着符号位变成了1，在上一章中也提到了，有符号正数相加溢出时只能发生符号位由0变为1（推导过程见上一章）。综上，正数加正数超限就是其和符号位变为1。
那么负数加负数呢，负数最小值为$?2^{n?1}$二进制为$1(符号位)0000\dots 000（n?1个0）$两个最大值相加符号位变为0，$?2^{n?1}?1$同理。
综上两种情况，可以设计出使用一位符号位判断溢出的方法。设两个加数的符号位分别是——$X_1$和$X_2$，运算和的符号位设为$S$,正数相加判断溢出的逻辑表达式：
$$X_1{X}_2\overline{S}$$
负数相加判断溢出逻辑表达式：
$$\overline{X_1}\overline{X_2}S$$
综上，一位符号判断溢出的逻辑表达式为：
$$OverFlow=\overline{X_1}\overline{X_2}S+X_1{X}_2\overline{S}$$

$OverFlow=0$表示无溢出，$OverFlow=1$表示无溢出。

---

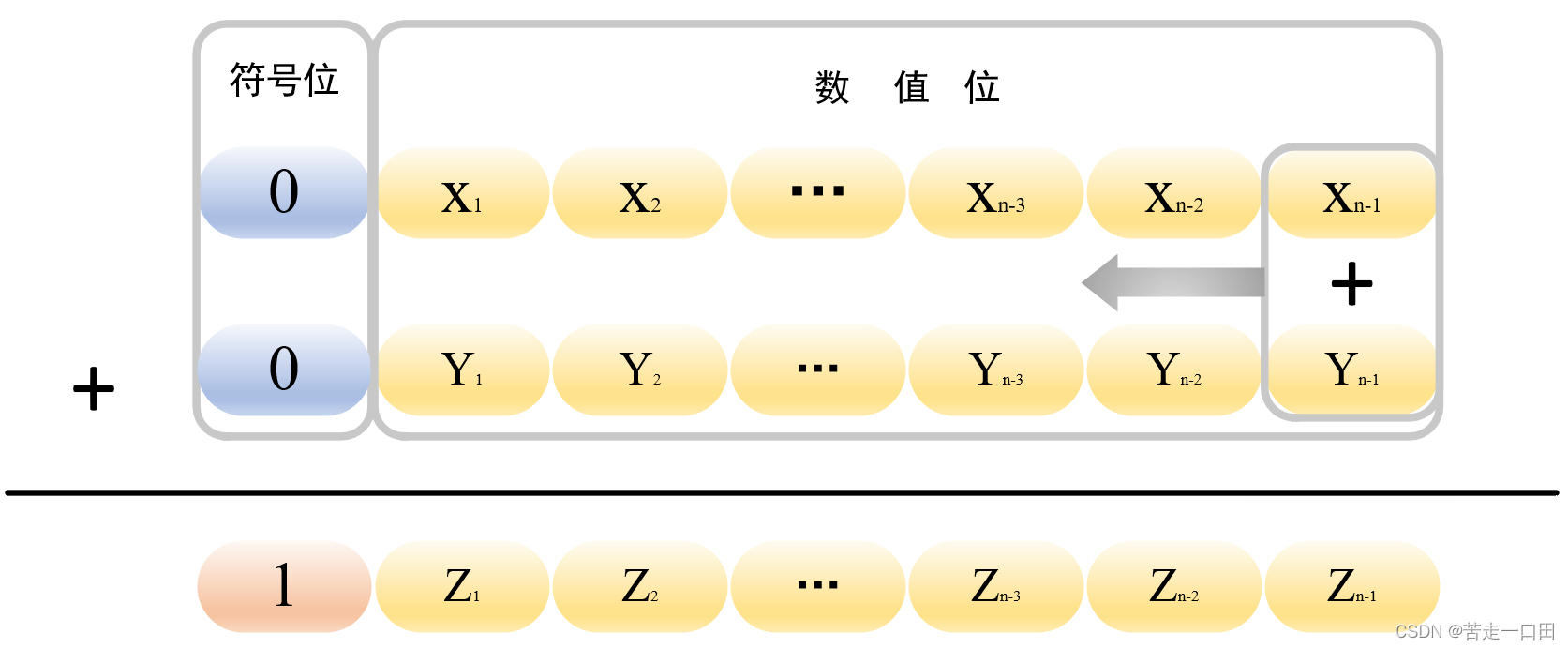
2.采用一位符号和进位
使用一位符号可以判断是否溢出，当然，也可以在运算过程中直接判断是否溢出，这里还是分两种情况讨论。正数加法运算发生溢出时符号位发生变号，意味着数值位的最高位发生进位。从低位开始逐位相加，发生溢出的情况就是相加到数值位的最高位后发生进位（正数相加不会出现进位两次的情况）。如下：

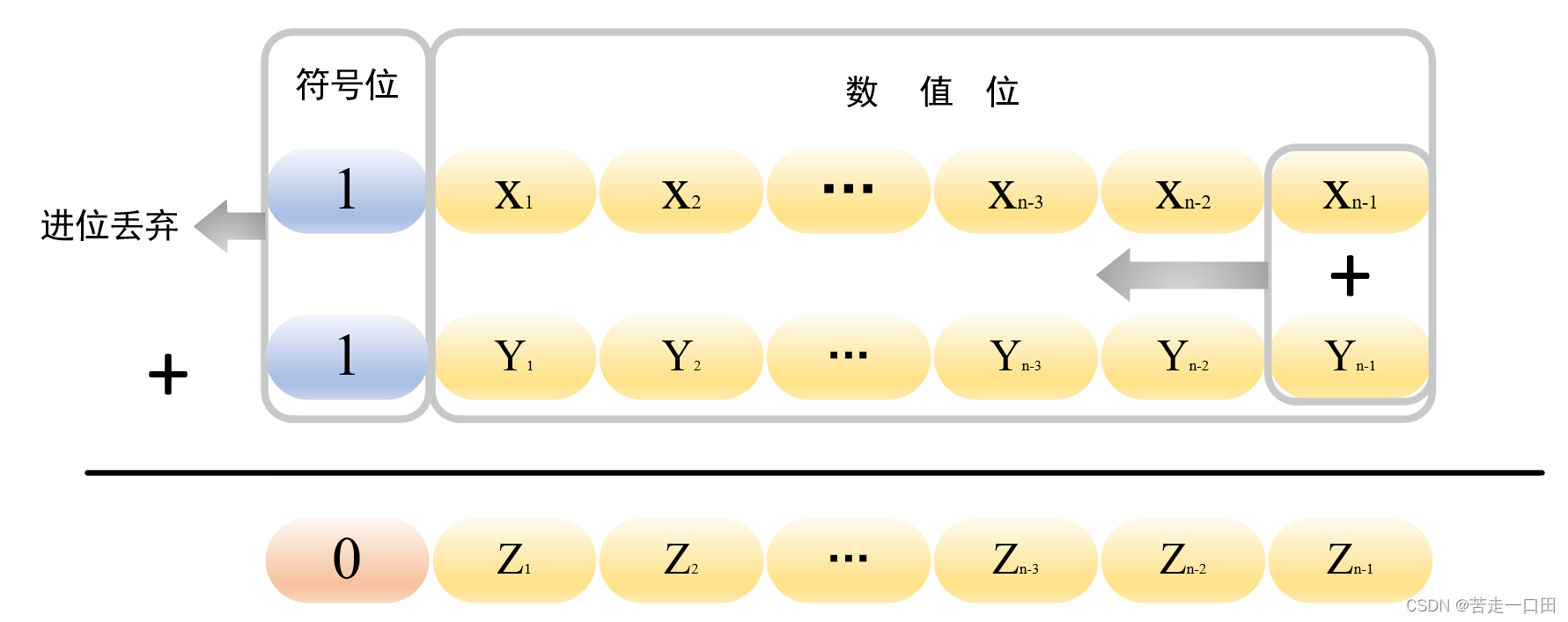
负数相加发生溢出时，意味着数值位最高位没有发生进位，从最低位开始相加，发生溢出时数值位的最高位不发生进位，如下：

综合正数相加和负数相加两种情况，使用$C{F}_1$和$C{F}_2$分别表示符号位和数值部分最高位的进位标记（例如CF_1=1，表示符号位发生进位）只有符号位的进位与数值位最高位的进位情况相同才表明没有溢出。
综上，逻辑表达式为：
$$OverFlow=C{F}_1\oplus C{F}_2$$
$OverFlow=0$表示无溢出，$OverFlow=1$表示无溢出。
这里需要注意$C{F}_2$，数值位的最高位是否进位需要从最低位开始进行加法运算才可以确定，并与可以使用数值部分的最高位直接相加判断$C{F}_2$。此外
这种方法也可以判断无符号数的溢出情况——将此时的符号位与数值的最高位看作无符号数的最高位与次高位即可。

---

3.采用双符号位
使用以上两种方法可以简单的判断是否发生溢出，但是都需要同时存储两个加数和结果，在硬件设计时，就需要考虑加法电路的存储效能，此外，一位符号的判断方法需要使用两个加数和结果才能确定溢出的类型——正溢出与负溢出（或者叫上溢出和下溢出）。在一位符号和进位判断溢出方法的基础上设计一种新的运算符——双符号位判断溢出。
双符号位的理解方式有很多，这里介绍一种个人觉得比较合适的理解方向。双符号位将进位符纳入符号位，这样可以直接在运算结果中判断溢出情况。使用“00”表示正数，“11”表示负数。
这里还是分两种情况：

• 正数加正数：
  根据以上一位符号与进位判断溢出过程的分析，正数加正数发生溢出也就是数值位最高位发生进位，如下
  
• 负数加负数：
  根据以上一位符号与进位判断溢出过程的分析，负数加负数发生溢出也就是数值部分的最高位不发生进位，如下
  所以通过双符号的区别就可以区分溢出的区别——
  (1) “01”表示正溢出，
  (2) “10”表示负溢出，
  (3) “00”表示结果为正，
  (4) “11”表示结果为负。

---

变形补码的补充：双符号位表示的补码也称变形补码也叫模4补码，变形补码的定义如下：

• 小数
  
  $$x_{补码}=x_{真值}mod4=\{\begin{array}{l}x,1>x\ge 0\\ 4+x=4?|x|,0>x\ge ?1\end{array}\text{\hspace{1em}(1)}$$
  
• 整数
  
  $$x_{补码}=x_{真值}mod(2^n)=\{\begin{array}{l}00,x{2}^{n?2}>x\ge 0\\ 2^n+x=2^n?|x|0>x\ge ?2^{n?2}\end{array}\text{\hspace{1em}(2)}$$
  
  变形补码小数定义与一位符号的补码定义不同，而整数的定义在形式上是相同的（相同机器字长下，变形补码与一位符号补码整数能够表示的长度不同）。
  这里注意一点，双符号位在一般内存中并不会这么存储，因为只要计算正确运算结果“00”和“11”表示正负和“0”“1”，在ALU中（算术逻辑单元），运算时一般会额外增加一位作为辅助位补充单符号位。
  总而言之，溢出主要针对

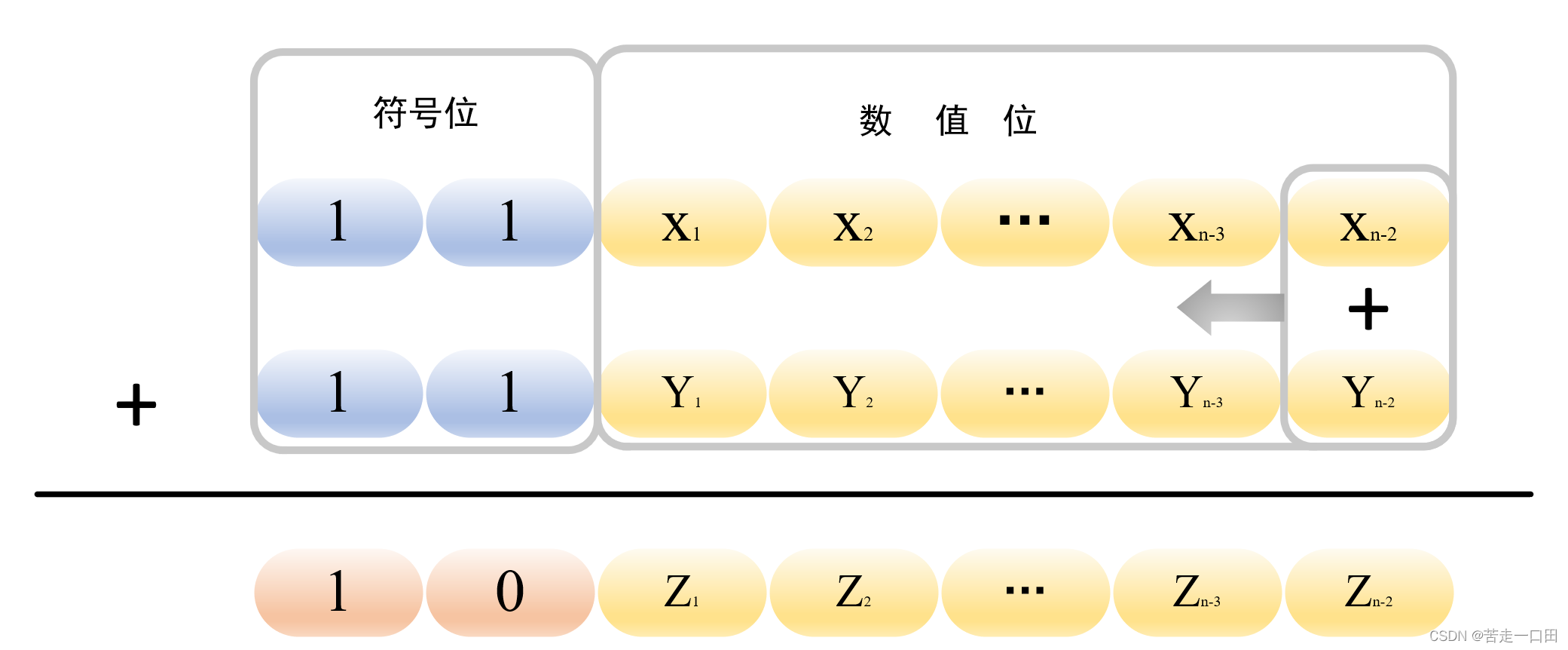
1.5 定点数的加法

首先申明，具体的运算解析以有符号数为主，无符号数需要讨论的内容并不多

在上一篇文章中讲解补码时已经讲解过使用补码运算代替原码运算的原理，（看上一章内容点这里👉： 上一章）
这里直接给出补码的运算
如果上一章的内容理解了，这里补码的加法就并不难了
这里给出补码运算的符号记法：
X 真 值 1 ± X 真 值 2 = { （ X 真 值 1 ） 补 码 + ( ± X 真 值 2 ) 补 码 } m o d ? 2 n ( 定 点 小 数 模 2 ) X_{真值1}\pm X_{真值2}=\{（X_{真值1}）_{补码}+(\pm X_{真值2})_{补码}\}mod\:2^n(定点小数模2) X真值1?±X真值2?={（X真值1?）补码?+(±X真值2?)补码?}mod2n(定点小数模2)
做加法时，两者补码直接相加，相减时，被减数补码加上减数相反数的补码。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖