[C++知识库] P1035 [NOIP2002 普及组] 级数求和

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> C++知识库 -> P1035 [NOIP2002 普及组] 级数求和 -> 正文阅读

[C++知识库]P1035 [NOIP2002 普及组] 级数求和

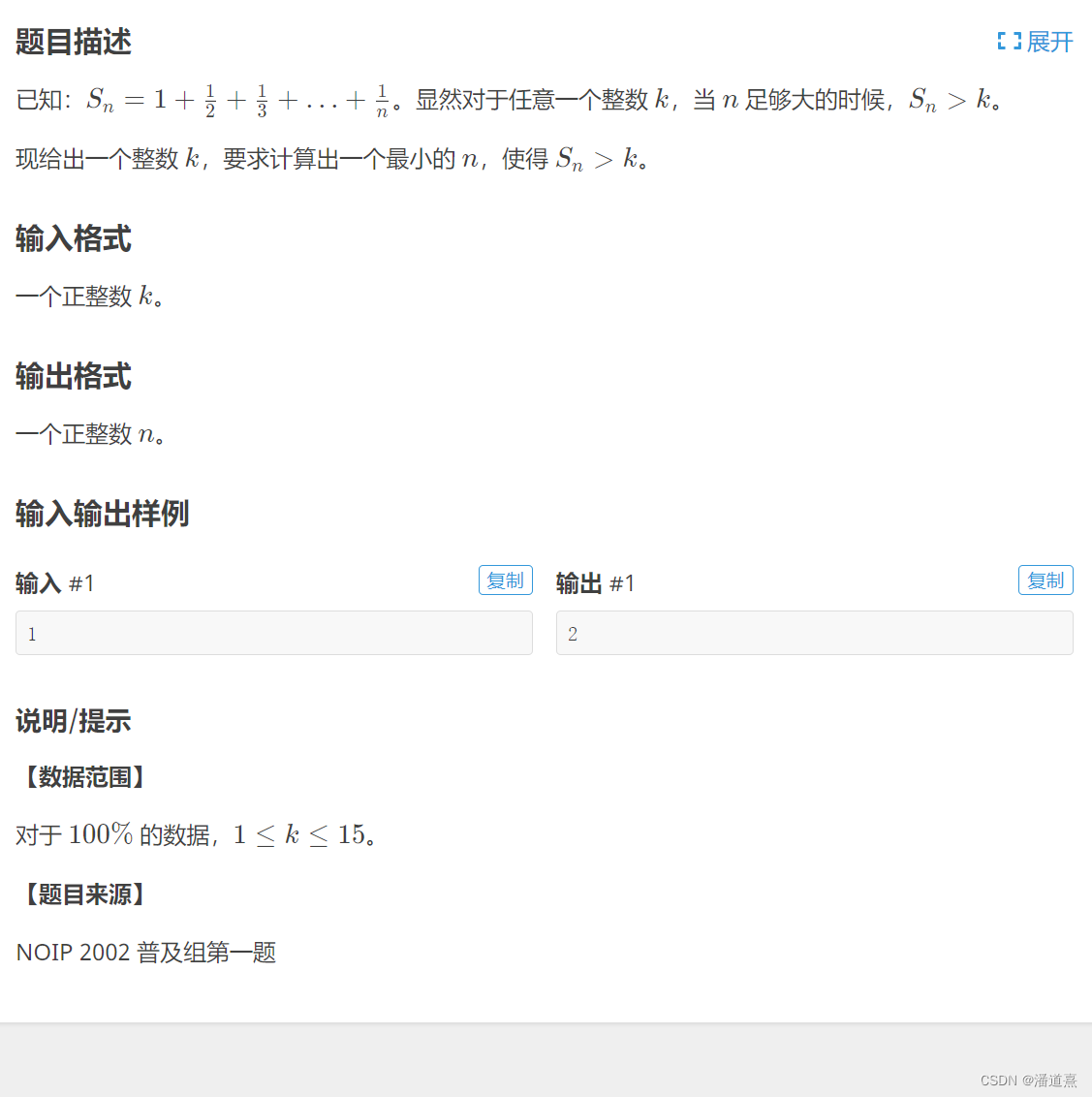
在这里插入图片描述
简单至极。

//Author:PanDaoxi 
#include <iostream>
using namespace std;
int main(){
	double k,n=0.0,s=0.0;
	cin>>k;
	while(1){
		s+=1/(++n);
		if(s>k) break;
	}
	cout<<n;
	return 0;
}

其他解法：（选自洛谷大神 Vel_ 的博客）
这是优化的程序。

以后可能会将回归性函数称为器，分类性函数称为灯。

#include<bits/stdc++.h>
using namespace std;

bool excess(double sn,double k){ //溢出灯
	return sn > k;
}

int main(){
	int i=1;
	double sn=0,k;
	cin>>k;
	while(1){ //累加器
		sn += (double)1/(double)(i++);
		if(excess(sn,k)) {cout<<i-1;break;}
	}
	return 0;
}

数论优化 O(logk) O(logk)

https://www.luogu.org/problemnew/solution/P1035

exp(k)是指数调用的复杂度，最高可以优化到log(k)（相当多项式幂），因此最后得到的复杂度为O(logk)O(logk)。

值得指出的O(logk)O(logk)仅仅是理论的，因为最后cout打印的数的宽度已经是O(k)了！

运算虽然可以很快，却会被输出所限制。

#include<bits/stdc++.h>
using namespace std;

bool excess(double sn,double k){
	return sn > k;
}

int main(){
	int i=1;
	double k;
	while(cin>>k){
		cout<<floor(exp(k-0.5772156649) + 0.5)<<endl;
	}
	return 0;
}