热身赛
A.
虽然计算几何学了和没学差不多,但是板子题还是要会的(火速去补)
一定能形成折线,所以选最长的两个删掉就可以了
struct node {
double dist;
int x;
};
int sat[maxn];
vector<node> v;
double div(int x1, int y1, int x2, int y2) {
double temp = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
return temp;
}
bool cmp(node a, node b) {
return a.dist > b.dist;
}
int main() {
IOS;
int n;
cin >> n;
remax(sat);
sat[0] = 0;
double sum = 0;
for (int i = 1; i <= n; ++i) {
cin >> sat[i];
sum += div(i - 1, sat[i - 1], i, sat[i]);
}
sat[n + 1] = 0;
sum += div(n + 1, sat[n + 1], n, sat[n]);
for (int i = 1; i <= n; ++i) {
double dist = div(i - 1, sat[i - 1], i, sat[i]) + div(i + 1, sat[i + 1], i, sat[i]);
v.push_back({dist, i});
//cout << dist << endl;
}
sort(v.begin(), v.end(), cmp);
int cnt = 0;
double dis1, dis2;
int x1, x2;
for (auto w : v) {
if (cnt == 0)
dis1 = w.dist, x1 = w.x;
else if (cnt == 1)
dis2 = w.dist, x2 = w.x;
else
break;
++cnt;
}
if (x1 > x2)
swap(x1, x2);
if (x1 + 1 == x2) {
double temp = div(x1, sat[x1], x2, sat[x2]);
sum = sum - dis1 - dis2 + temp;
sum += div(x1 - 1, sat[x1 - 1], x2 + 1, sat[x2 + 1]);
} else {
sum -= dis1;
sum += div(x1 - 1, sat[x1 - 1], x1 + 1, sat[x1 + 1]);
sum -= dis2;
sum += div(x2 - 1, sat[x2 - 1], x2 + 1, sat[x2 + 1]);
}
cout << sum;
return 0;
}
B.我不理解
题解:https://blog.csdn.net/qq_35630119/article/details/121584461
C.计算几何,挣扎看了看过了的,超出了能力范围
正式赛
D.
我以为是解二元二次方程组,直接放弃;又没想到简单推一下就行
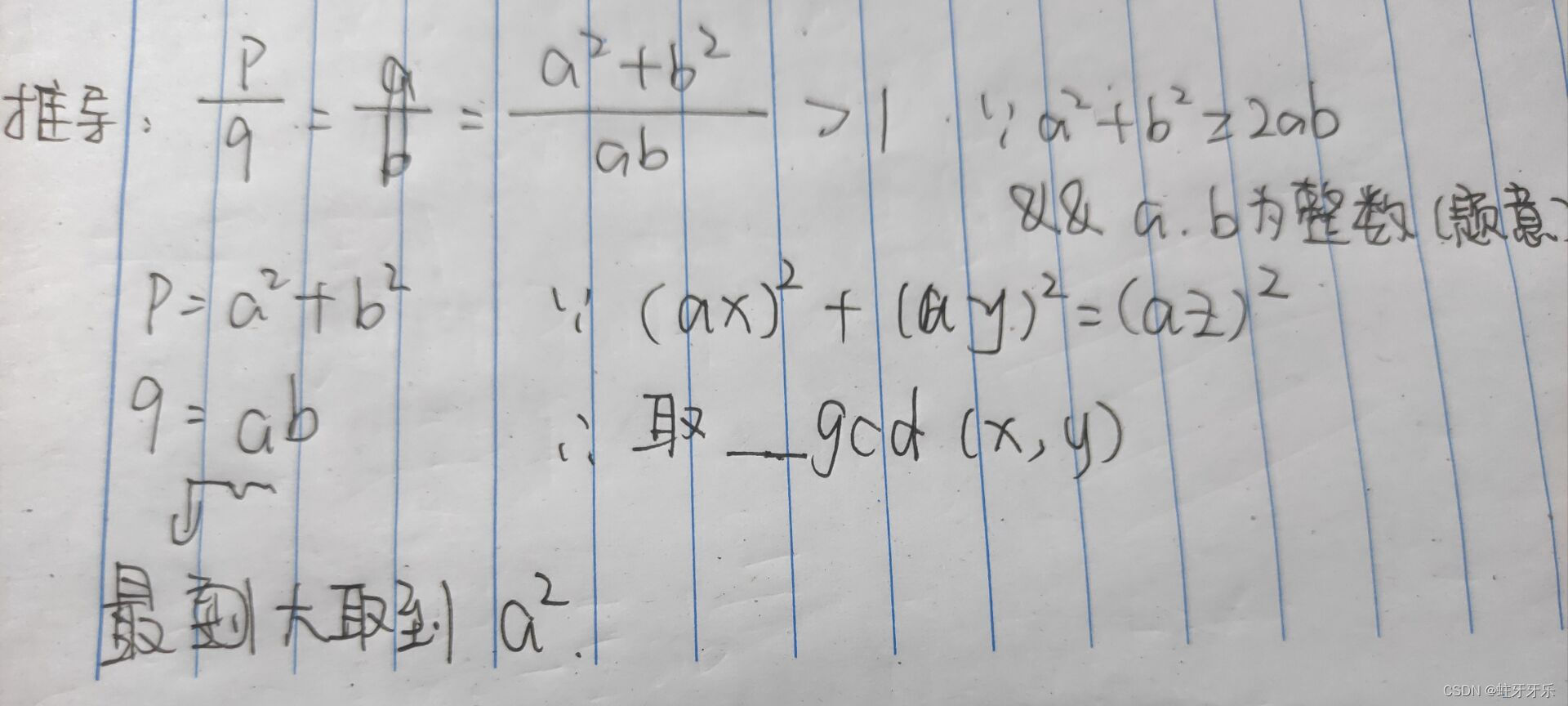
ll a, b;
bool solve(){
int d = __gcd(a, b);
a /= d, b /= d;
for (int i = 1; i <= sqrt(b); ++i){
if(b % i == 0){
ll t = b / i;
if(t * t + i * i == a){
cout << i << " " << t << endl;
return false;
}
}
}
return true;
}
int main() {
IOS;
// freopen("P1908_6.in","r",stdin);//读入数据
// freopen("P1908.out","w",stdout); //输出数据
int t;
cin >> t;
while(t--){
cin >> a >> b;
if(solve()){
cout << "0 0" << endl;
}
}
return 0;
}
E.
这题比上一题简单
满足第二小的和最小的相差大于等于k,其它相差一定大于k
ll a[maxn];
map<ll, bool> mp;
int main() {
IOS;
// freopen("P1908_6.in","r",stdin);//读入数据
// freopen("P1908.out","w",stdout); //输出数据
int n, k;
cin >> n >> k;
int cnt = 0;
for (int i = 0; i < n; ++i){
ll t;
cin >> t;
if(!mp[t]){//去重 3 3这种没意义
a[cnt++] = t;
mp[t] = true;
}
}
sort(a, a + cnt,greater<int>());
ll ans = 0;
ll pre = -1;
for (int i = 0; i < cnt; ++i){
if(pre == -1 || pre - a[i] >= k){
++ans;
pre = a[i];
}
}
cout << ans;
return 0;
}
