质数定义

一个大于1的自然数

“质数又被称为素数，是指一个大于1的自然数，除了1和它自身外，不能被其它自然数整除。

反比例函数

比如我们需要判断数m(m>1)是不是质数。

对于我们来说m就是一个定值，需要找出所有两个数相乘为m的所有可能，我们设其中一个因数为x,另一个因数为y，因此x，y满足xy=m变换为y = m/x。

y = m/x函数形式不错就是我们数学中所学的反比例函数，好的我们画出此函数。

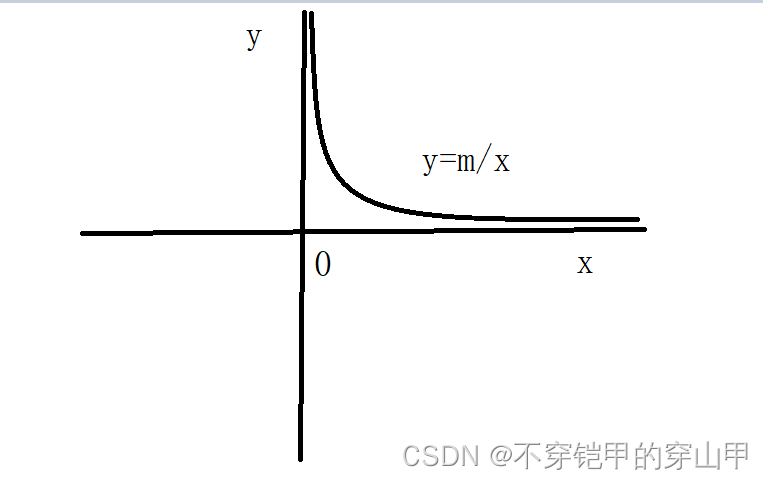
我们只需从该函数中找出x,y相乘，积为m的二元有序对（x,y）即可。

那和算数平方根由什么关系呢？

我们根据数学知识可知，y = m/x（m>1）反比例函数是关于y=x对称，因此我们画出y=x。

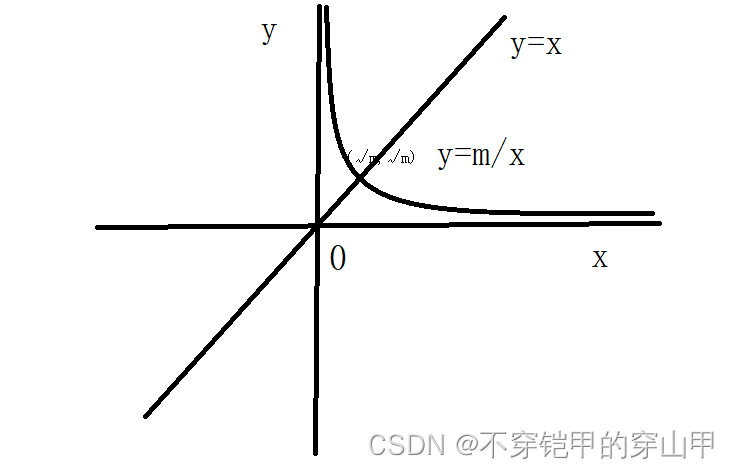
根据y=m/x,y=x我们可以求出交点（√m，√m）,

关于y=m/x反比例函数关于y=x对称，在y=m/x上的任意一点(x0,y0),关于y=x的对成点为(y0,x0),两点(x0,y0)，(y0,x0)分别在（√m，√m）的左右，又因为x0*y0=y0*x0=m，也就是说我们在交点（√m，√m）左边找到的(x0,y0)满足x0*y0=m，也能在（√m，√m）右边找到与之唯一对应的点(y0,x0)满足y0*x0=m。

判断质数不考虑两个因数的顺序问题，所以根据以上描述我们只需在x<=√m的范围判断是否存在(x,y)满足 x,y是正整数，并且x,y≠1的二元有序对，如果不存在则为质数，否则为合数。

代码

#include <stdio.h>
#include <math.h>

int isPrime(int n) {
    if (n < 2) {
        return 0;
    }
    for (int i = 2; i <= sqrt(n); i++) {
        if(n % i == 0) {
            return 0;
	    }
    }
    return 1;
}

int main() {
    for (int i = 101; i <= 200; i++) {
        if (isPrime(i)) {
            printf("%d\n", i);
        }
    }
    return 0;
}