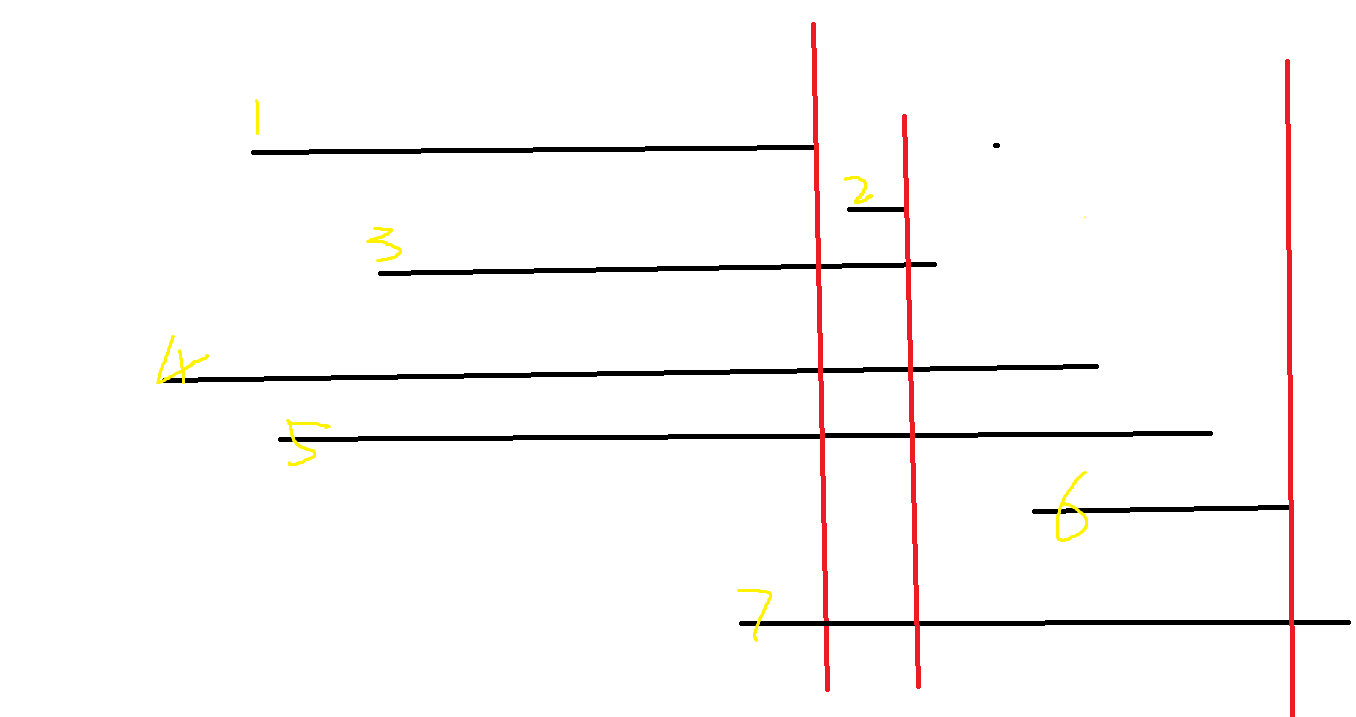
假设黑线为给定区间按右端点排序后的结果,我们以第一条线的右端点为基准画一条垂直的红线,该红线与1,3,4,5,7五条黑线相交,这意味着这五个区间我们只能选择一个,显然,此时选择第一个区间是最优的,因为它的右端点最靠左。
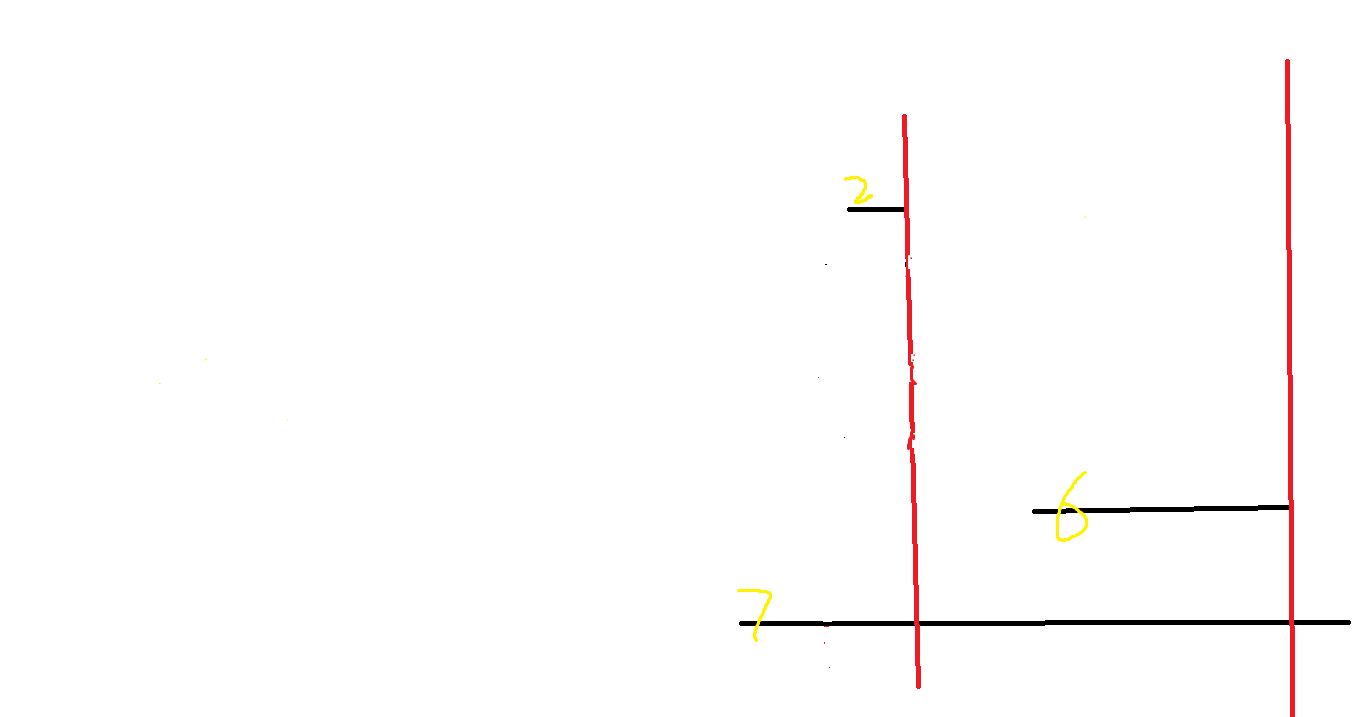
接下来,我们排除掉这五条黑线,只考虑剩下的黑线,按照同样的方法分析,最后我们会发现,选出来的线和从第一条线遍历到最后一条线,能选就选的结果是一样的。
#pragma GCC optimize("Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
#define BEGIN signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define END return 0;}
#define endl '\n'
#define sqr(x) ((x)*(x))
#define lowbit(x) ((x)&-(x))
typedef long long ll;
typedef unsigned long long ull;
template<class T>void read(T& x)
{
x=0;int f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
x*=f;
}//快读
template<class T>void write(T& x)
{
int num=0;char c[40];
while(x)c[++num]=(x%10)+48,x/=10;
while(num)putchar(c[num--]);
}//快写
const int N = 2e6 + 10;
int n, m;
struct Node
{
int l, r;
bool operator<(const Node& node)const{
return r < node.r;
}
}a[N];
BEGIN
#ifdef FSLSE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
// 手动修改栈内存
int size=64<<20; // 申请64MB栈空间
// 32位Windows使用
// __asm__("movl %0, %%esp\n"::"r"((char*)malloc(size)+size));
// Linux以及64位Windows使用
__asm__("movq %0, %%rsp\n"::"r"((char*)malloc(size)+size));
#endif
cin >> n >> m;
for (int i = 1;i <= n;++i)cin >> a[i].l >> a[i].r;
sort(a + 1, a + 1 + n);
// for (int i = 1;i <= n;++i)cout << a[i].l << ' ' << a[i].r << endl;
int ans = 1, last = 1;
for (int i = 2;i <= n;++i)
if (a[last].r <= a[i].l)++ans, last = i;
cout << ans << endl;
#ifdef FSLSE
exit(0); // 手动修改栈内存时一定要有exit(0)
#endif
END
