A. Prof. Slim
题意
给定长度为n的整数序列a1—an,每次可以进行如下两种操作中的一个:
- 互换两个不同符号元素的符号(即:把一个正数和一个负数变成他们的相反数)
- 选择两个元素,使他们拥有不同符号
问:能否通过有限次操作把序列a1—an变成单调不下降序列?
思路
负号的数量是恒定的,把所有的m个负号给最前面的m个元素,然后判断是否可行即可。
代码实现
void solve() {
int t = 0;
cin >> t;
while (t--)
{
int n = 0;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
int num = 0;//记录有几个负号
for (int i = 1; i <= n; i++)if (a[i] < 0) num++;
for (int i = 1; i <= n; i++){
if (i<=num) {
if (a[i] > 0) a[i] *= (-1);
}
else {
if (a[i] < 0) a[i] *= (-1);
}
}
//cout << num << ' ';
bool flag = true;
for (int i = 1; i <= n-1; i++)
{
if (a[i + 1] < a[i]) {
flag = false;
break;
}
}
if (flag) cout << "YES\n";
else cout << "NO\n";
}
return;
}
B. Dorms War
题意
给定长度为n的字符串s,给定k个特殊字符。每次可以删掉s中所有特殊字符之前相邻的一个元素,当最后存留下来的特殊字符前都没有相邻元素时,再删除就会报错。
问:最多进行多少次删除操作可以不报错。
思路
看看样例2和样例3:

发现决定删除次数的是最长的特殊字符间隔
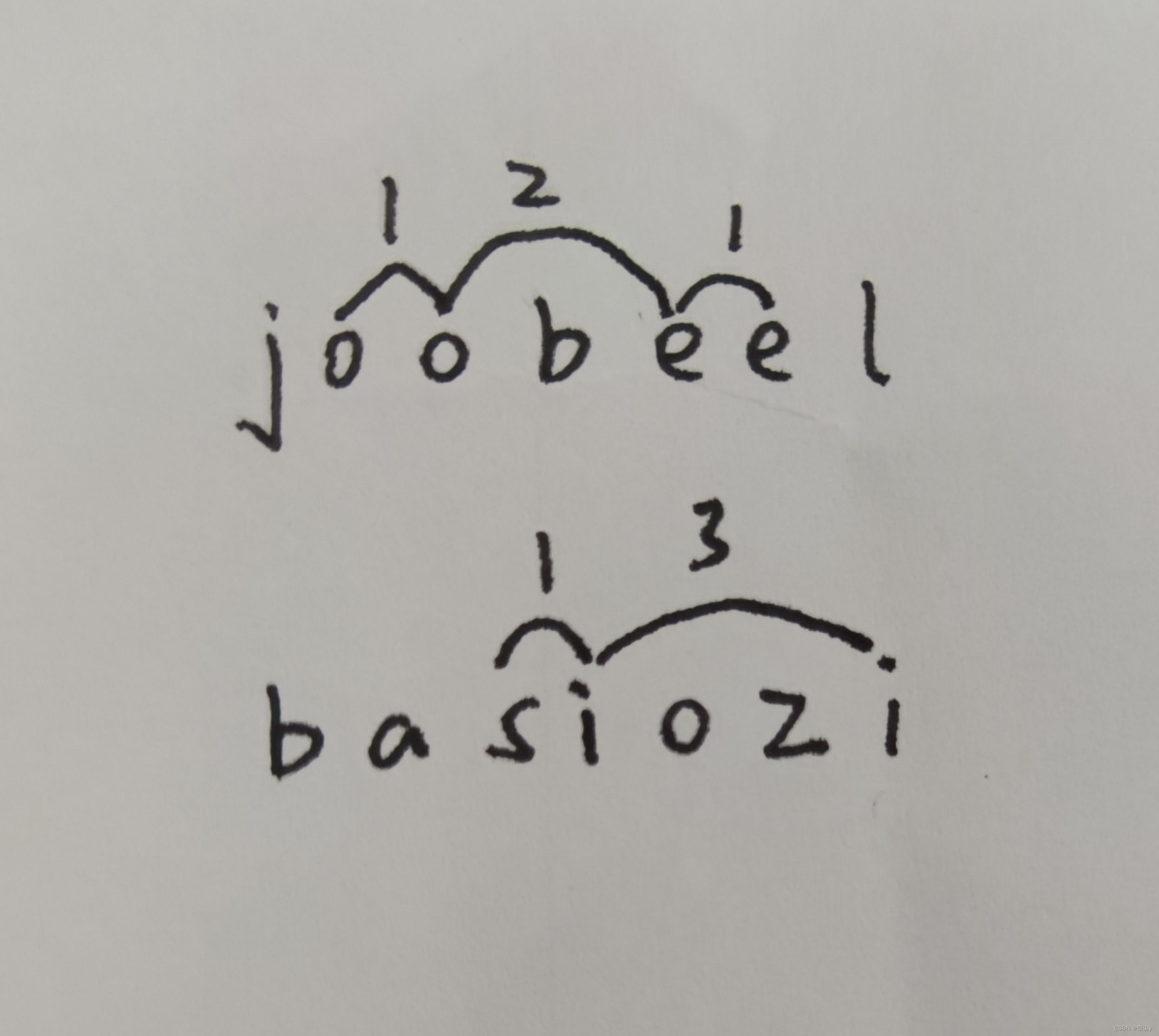
ok,答案就是最长的特殊字符间隔长度+1。
思考为什么:每次删除会删除特殊字符之前的一个数,那么最长间隔之间的字符一定是最后被删完的(右端的特殊字符在此过程中会被替换,但对答案没有影响),因此删除的最大次数就是最长的特殊字符之间的字符数+1(包括左端特殊字符自己)。
代码实现
void solve() {
int t = 0;
cin >> t;
while (t--)
{
int n = 0;
op.clear();
memset(s, 0, sizeof s);
cin >> n >> op;
int k = 0;
cin >> k;
for (int i = 0; i < k; i++) cin >> s[i];
int maxn = 0;
int num = 0;//记录有几个特殊字符
int pre = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < k; j++)
{
if (op[i] == s[j]) {
num++;
maxn = max(maxn, i - pre);
pre = i;
break;
}
}
}
cout << maxn << endl;
}
return;
}
C. Where is the Pizza?
题意
给定长度为n的1-n之间的排列a(a1—an)和排列b(b1—bn),以及长度为n的未给定的排列c(c1—cn).
排列:长度为n的排列表示1—n之间数字的乱序组合。
序列c具有以下性质:
- ci = ai or bi
- 部分ci已给定
询问ci有多少种可能方案(答案很大,所以要对1e9+7取模)
思路
观察第一个样例,发现:
1
—
—
2
—
—
3
成
环
4
—
—
7
成
环
5
—
—
6
成
环
1——2——3成环\\ 4——7成环\\ 5——6成环
1——2——3成环4——7成环5——6成环
对于每个环,发现一个元素确定选择后其他位置的元素也随之确定,因此有n个环,就有2^n种方案。
考虑没有贡献的环:
-
c排列中某些位置给定了元素,对应的环的元素选择已经确定,对答案的贡献为0,因此不需要考虑。
-
自环对答案没有贡献,也不需要考虑
代码实现
//用并查集来维护环
#include<cstdio>
#include<iostream>
#include<map>
#include<algorithm>
#include<cmath>
#include<vector>
#include<set>
#include<cmath>
#include<cstring>
using namespace std;
const int INF = 1e9;
typedef long long ll;
const int N = 1e5 + 10;
const int mod = 1e9 + 7;
int p[N];//维护并查集
int siz[N];//记录每个并查集的大小(如果为2则贡献为0)
int a[N], b[N], c[N];
bool is_valid[N];
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];//找到祖宗节点
}
void solve() {
int t = 0;
cin >> t;
while (t--)
{
//memset(is_valid, true, sizeof is_valid);
int n = 0;
cin >> n;
for (int i = 1; i <= n; i++)
{
siz[i] = 0;
is_valid[i] = true;
p[i] = i;
}
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
cin >> b[i];
}
for (int i = 1; i <= n; i++) cin >> c[i];
for (int i = 1; i <= n; i++)
{
p[a[i]] = find(b[i]);//建环
}
for (int i = 1; i <= n; i++)
{
if (c[i] != 0) is_valid[find(a[i])] = false;
siz[find(a[i])] += 2;
}
int res = 1;
for (int i = 1; i <= n; i++)
{
int m = find(a[i]);
if (is_valid[m])
{
if (siz[m] > 2)res = (res * 2) % mod;//自环只有一种选择,对答案没有贡献
//cout << "siz" << m << "=" << siz[m]<<' ';
}
is_valid[m] = false;
}
cout << res<<endl;
}
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
solve();
return 0;
}
D. Very Suspicious
题意
询问至少要画几条直线才能在无限六边形中划分出至少n个等边三角形。
思路
假设第i次画直线,该次画直线能够产生的最多的等边三角形数量=该条直线之前与此直线斜率不同的直线的数量*2(和每个斜率不同直线都相交产生两个等边三角形),因此记录斜率不同的三角形数量即可。
注意,本题要预处理出1e9内所有满足要求的直线数量,然后用二分查找,不然会tle。而且预处理时因为数组太大,要用vector
代码实现
vector<int> ans;
vector<int> cnt;
int num = 0;
int find(int x, int n)
{
int l = 0, r = n;
while (l < r)
{
int mid = l + r >> 1;
if (ans[mid] >= x) r = mid;
else l = mid + 1;
}
return l;
}
void solve() {
int num = 0;
for (int i = 1;1; i++)
{
if (i % 3 == 0) {
cnt.push_back(i / 3 * 2);
}
else cnt.push_back(i / 3 * 2 + (i - 1) % 3);
if (i >= 2) ans.push_back(ans[i - 2] + cnt[i - 1] * 2);
else ans.push_back(0);
num++;
if (ans[i - 1] >= 1e9 + 10) break;
}
//cout << num << ' ';
int t = 0;
cin >> t;
while (t--)
{
// 第i条直线和前面与它斜率不相同的每条直线相交都会出现两个等边三角形
// 不同的直线数量:x = i/3 * 2 + (i-1)%3
// 增加的三角形数:x*2
int n = 0;
cin >> n;
int res = find(n, num)+1;
cout << res << endl;
}
return;
}
