代码题
1. 老板发奖金
老板一共需要给某个员工发奖金n元,可以选择一次发1元,也可以选择一次发2元,也可以选择一次发3元。请问老板给这位员工发放完n元奖金共有多少种不同的方法?
数据范围:1 <= n <= 10
需要注意,一次性最多只能发三块
是青蛙跳台阶的类似问题,类比青蛙跳台阶问题来说的话就是每次可以跳一步、或者两步、或者三步,求到n阶台阶有几种跳法。
循环求解
#
#
# @param num_money int整型 奖金的总数,单位为元
# @return int整型
#
class Solution:
def CalulateMethodCount(self , num_money ):
# write code here
recur_add=0
f=[0 for _ in range(num_money+1)]
f[1]=1
f[2]=2
f[3]=4
for i in range(4,num_money+1):
f[i]=f[i-1]+f[i-2]+f[i-3]
return f[num_money]
如果没有这个一次性最多只能发三块的限制
1:先发1块的情况下,剩下4块是不是就和发4块的方法一样了?
2:先发2块的情况下,剩下3块是不是就和发3块的方法一样了?
3:先发3块的情况下,剩下2块是不是就和发2块的方法一样了?
4:先发4块的情况下,剩下1块是不是就和发1块的方法一样了?
5:5块一次性发完,唯一方法
即符合 f(n) = f(n-1) + f(n-2) + … + f(1) + 1=2f(n-1)
class Solution:
def CalulateMethodCount(self , num_money ):
# write code here
recur_add=0
f=[0 for _ in range(num_money+1)]
f[0]=1
f[1]=1
recur_add=f[0]+f[1]
for i in range(2,num_money+1):
f[i]=recur_add
recur_add+=f[i]
return f[num_money]
2.撤销与恢复
撤销/恢复操作具有广泛的用途,比如word文档中输入一个单词,可以点撤销,然后可以再恢复。
编程实现如下功能: 从标准输入读取到一个字符串,字符串可包含0个或多个单词,单词以空格或者tab分隔; 如果遇到 “undo” 字符串,表示"撤销"操作,前一个字符串被撤销掉; 如果遇到"redo"字符串,表示恢复刚才撤销掉的字符串.
例如: 输入字符串 “hello undo redo world.”, 对字符串中的 undo 和 redo 处理后, 最终输出的结果为 “hello world.”
先初始化两个栈stack和redo,然后利用双栈求解。遍历词表:
遇到普通词就压入stack,并清空redo栈,因为此时写入了一个新词,再往前的词已经找不回来了;
遇到undo就从stack中弹栈至redo;
遇到redo就从redo中弹栈至stack。
最终stack中的词就是最后保留下来的词
commands = input().strip().split(" ")
stack, redo = [], []
for cmd in commands:
if cmd == "undo":
if stack:
redo.append(stack.pop())
elif cmd == "redo":
if redo:
stack.append(redo.pop())
else:
redo.clear()
stack.append(cmd)
print(" ".join(stack))
3.密码生成
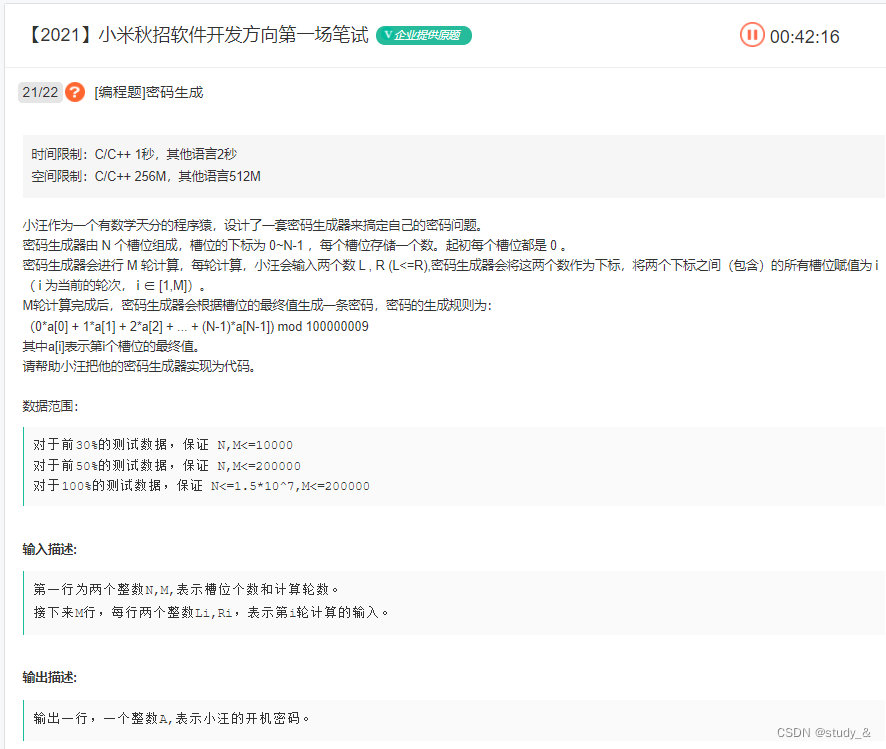
所谓取模运算,就是计算两个数相除之后的余数,符号是%。如a % b就是计算a除以b的余数。
直观想法
N,M=map(int,input().split())
s=[0 for _ in range(N)]
for i in range(M):
L,R=map(int,input().split())
s[L:R+1]=[i+1]*(R+1-L)
res=0
for i in range(N):
res+=i*s[i]
print(res%100000009)

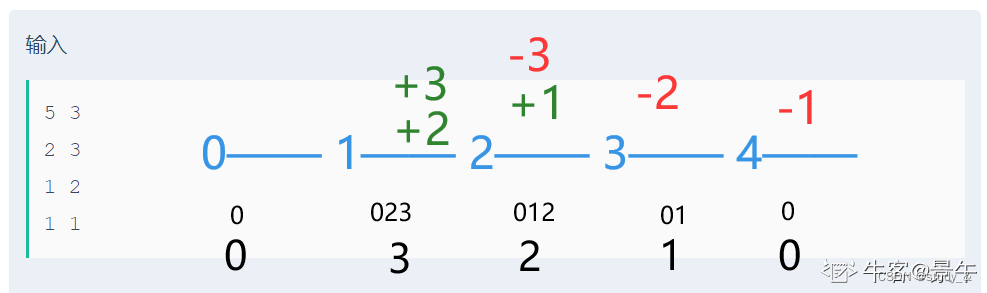
差分算法
用差分的思想。
创建数组存操作记录,在区间左端记录+i,区间右端记录-i。
创建一个优先队列,从左往右遍历所有操作,遇到+就add(i),遇到-就remove(i)。
每个位置的密码就是这时优先队列大顶端的数。
#include <bits/stdc++.h>
using namespace std;
const int mod = 100000009;
struct node {
int l, r, v;
};
bool operator <(node a, node b){
return a.v < b.v;
}
int main(){
int n, m;
while (cin >> n >> m) {
vector<int> v(n);
vector<node> tmp;
for (int i = 1; i <= m; i++) {
int a, b;
cin >> a >> b;
node now; now.l = a; now.r = b; now.v = i;
tmp.push_back(now);
}
sort(tmp.begin(), tmp.end(), [&](node &a, node &b) {
return a.l < b.l;
});
long long ans = 0;
priority_queue<node> q;
int pos = 0;
for (int i = 0; i < n; i++) {
while(i >= tmp[pos].l && pos < m) {
node now = tmp[pos];
q.push(now); #使用q来存储每个区间叠加的数
pos++;
}
while (!q.empty()) {
node now = q.top(); #优先队列大顶堆,取出最大的数
if (now.r < i) {
q.pop();
}
else {
v[i] = now.v;
break;
}
}
}
for(int i = 0 ;i < n; i++)
{
ans += i * v[i];
ans %= mod;
}
cout << ans << endl;
}
}
4. 最大体积值
一个长方体,长宽高都是质数,已知长宽高之和为n【n为[6,10000]范围内的自然数。】,求这个长方体的体积最大值。
输入值:长宽高之和。
输出值:体积的最大可能值。
示例:
输入:6 输出:8 说明:当长宽高都为2时体积最大,为8
简单说明
此题可分为两个部分:1. 质数数组生成 2. 三数之和为n
最后从符合三数之和为n的组合中找到体积最大的那组
#
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
#
# 得到体积的最大可能值
# @param n long长整型 长方形的长宽高之和。长宽高都为质数。
# @return long长整型
#
class Solution:
def getMaxVolume(self , n ):
# write code here
##质数数组
odd=[]
odd.append(1)
odd.append(2)
for i in range(2,n):
if list(set([i%j!=0 for j in range(2,i)]))==[True]:
odd.append(i)
##找到长宽高和符合要求的
possible=[]
for i in range(len(odd)):
left,right=i,len(odd)-1
while left<=right:
if odd[i]+odd[left]+odd[right]<n:
left+=1
elif odd[i]+odd[left]+odd[right]>n:
right-=1
else:
possible.append([odd[i],odd[left],odd[right]])
left+=1
right-=1
max_res=0
print(possible)
for i in range(len(possible)):
tmp=possible[i][0]*possible[i][1]*possible[i][2]
if tmp>max_res:
max_res=tmp
return max_res
参考
【1】牛客网
【2】
