
最简单的枚举就可以解决~~~~

?答案:20312088
#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
//每个点的坐标
struct node{
int x;
int y;
};
bool v[10000][10000]; //判断这个点有没有黑
int dist[10000][10000];
int dx[4]={-1,1,0,0};
int dy[4]={0,0,1,-1};
void bfs(){
memset(dist,-1,sizeof(dist)); //把每个点移动的长度初始化为-1
queue<node>q; //一个存点的数组
//把初始点x,y方向都向轴正方向平移3000 (这样才能保证它们不向负方向扩展,从而不会越数组的界)
q.push({3000,3000});dist[3000][3000]=0;
q.push({5020,3011});dist[5020][3011]=0;
q.push({3011,3014});dist[3011][3014]=0;
q.push({5000,5000});dist[5000][5000]=0;
//开始BFS
while(!q.empty()){
node t=q.front();
q.pop();
if(dist[t.x][t.y]==2020)return;//平移了2020,说明到了给的时间了
for(int i=0;i<4;i++){
int tx=t.x+dx[i];
int ty=t.y+dy[i];
if(tx<0 || tx>10000 || ty<0 || ty>10000)continue;// 相当于剪枝了
if(v[tx][ty] || dist[tx][ty]!=-1)continue; //扩散的这个点已经是黑色了或者这个点是别人扩散来的
//(只看每个点自己扩散出来的是不是达到了2020次,避免考虑点与点之间的扩散重合)
v[tx][ty]=true;
q.push({tx,ty});
dist[tx][ty]=dist[t.x][t.y]+1;
}
}
}
int main(){
v[3000][3000] = true;
v[5020][3011] = true;
v[3011][3014] = true;
v[5000][5000] = true;
bfs();
int ans = 0;
for (int i = 0; i < 10000; i ++)
for (int j = 0; j < 10000; j ++)
if(v[i][j]) ans ++; //看2020分钟有多少个黑色块
cout << ans << endl;
return 0;
}
答案:39001250856960000?
【唯一分解定理】任何大于1的正整数都能唯一地被分解为有限个质数的乘积
所以任何一个合数都可以被分解成几个质数相乘的形式【分解质因数】

阶乘约数,就是阶乘中所有数质因数分解后,质因数的出现的次数(幂数)+1相乘?
?代码思路:
1.分解质因数:一个数i的质因数,j从2到i,i/j==0则是约数,i=i/j,将已经分解的数去除,比如8/2=4,4/2=2,2是最后一个,最后得出8=2*2*2。
2.将分解质因数出现次数存放在一个数组中,循环将他们次数+1,然后相乘即可。
#include <iostream>
using namespace std;
int p[100];
int main()
{
//把2~100每一个数都进行分解质因数,并统计每一个质数出现的次数
for (int i = 2; i <= 100; i ++)
{
int n = i;
for (int j = 2; j <= n / j; j ++)
while(n % j == 0)
{
p[j] ++;
n /= j; //这一步是为了将已分解出的数去除
}
if(n > 1) p[n] ++;
}
long long ans = 1;
for (int i = 2; i <= 100; i ++)
if(p[i]) ans *= (p[i] + 1);
cout << ans << endl;
return 0;
}

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
答案:3616159
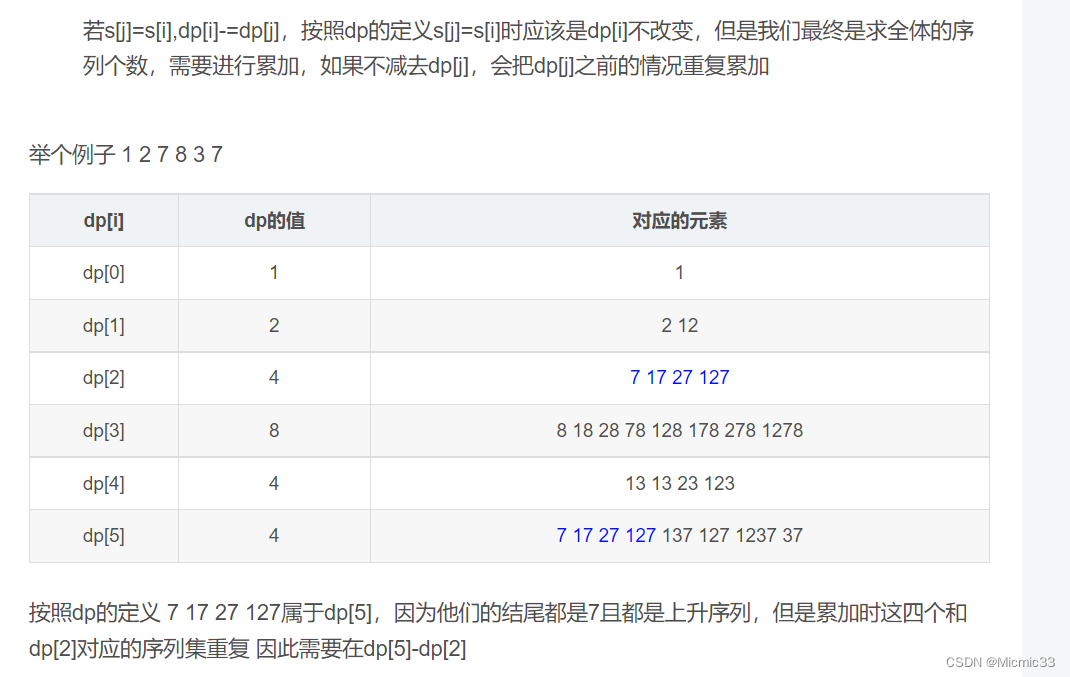
其实就是,如果以i结尾能接上子序列j,那么这就是一个新的子序列,只需加上这个子序列的种类数即dp[j]
当s[i]==s[j],说明以i结尾等价于以j结尾,逻辑上来说,不要这个结果就行,但实际上前指针在移到j前已经加过了d[j]的数量,显然和以前重复了一遍,所以-d[j]
#include<iostream>
#include<string>
using namespace std;
const int N=200;
int dp[N]; //dp[i]代表到s[i]的上升序列个数
int main(){
string s="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
for(int i=0;i<N;i++)dp[i]=1; //以每个字符为结尾的至少是1
for(int i=1;i<N;i++){
for(int j=0;j<i;j++){
if(s[i]>s[j])
dp[i]+=dp[j]; //可以接上
else if(s[i]==s[j])
dp[i]-=dp[j]; //避免重复
}
}
int ans=0;
for(int i=0;i<N;i++){
ans+=dp[i]; //求和
}
cout<<ans;
}