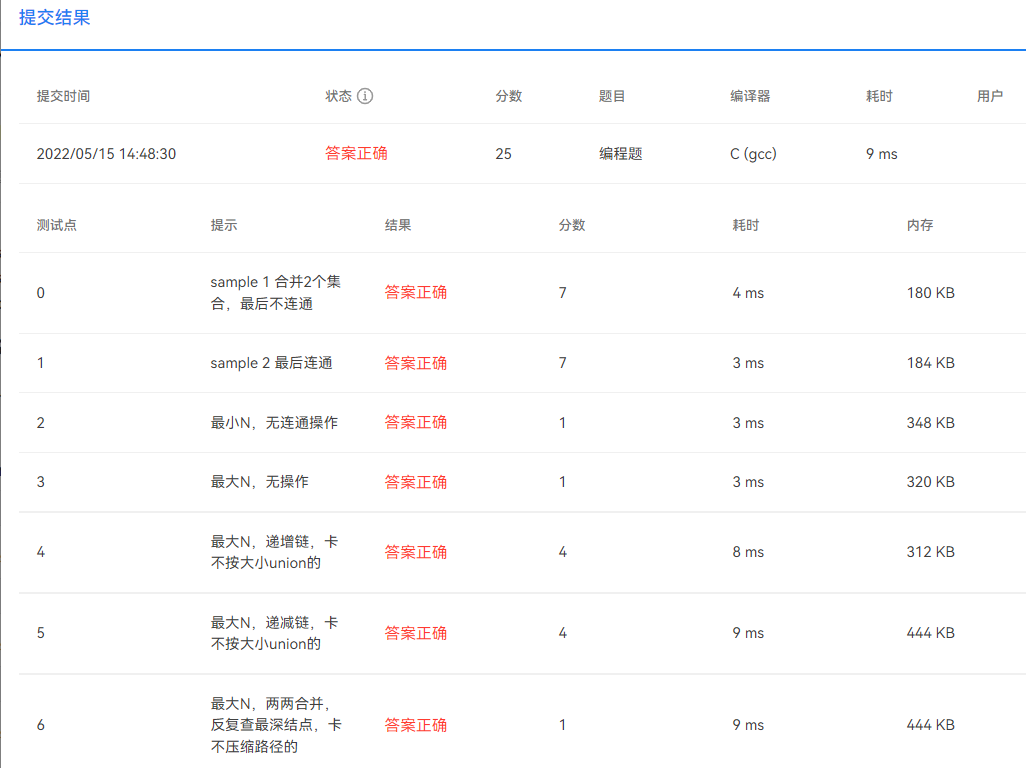
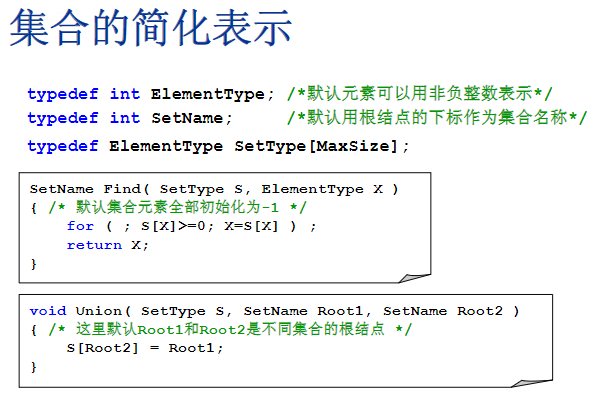
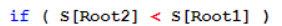集合的简化表示
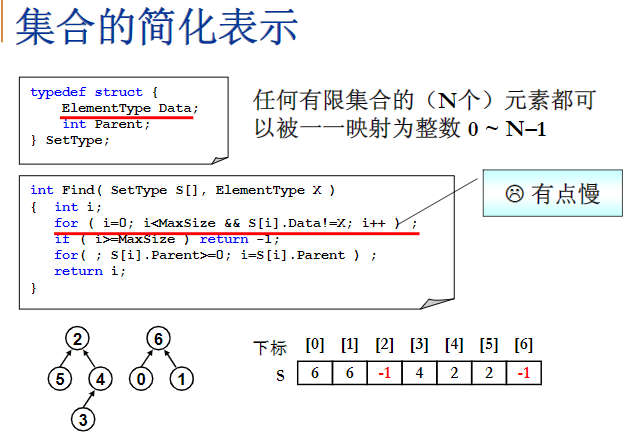
题意理解
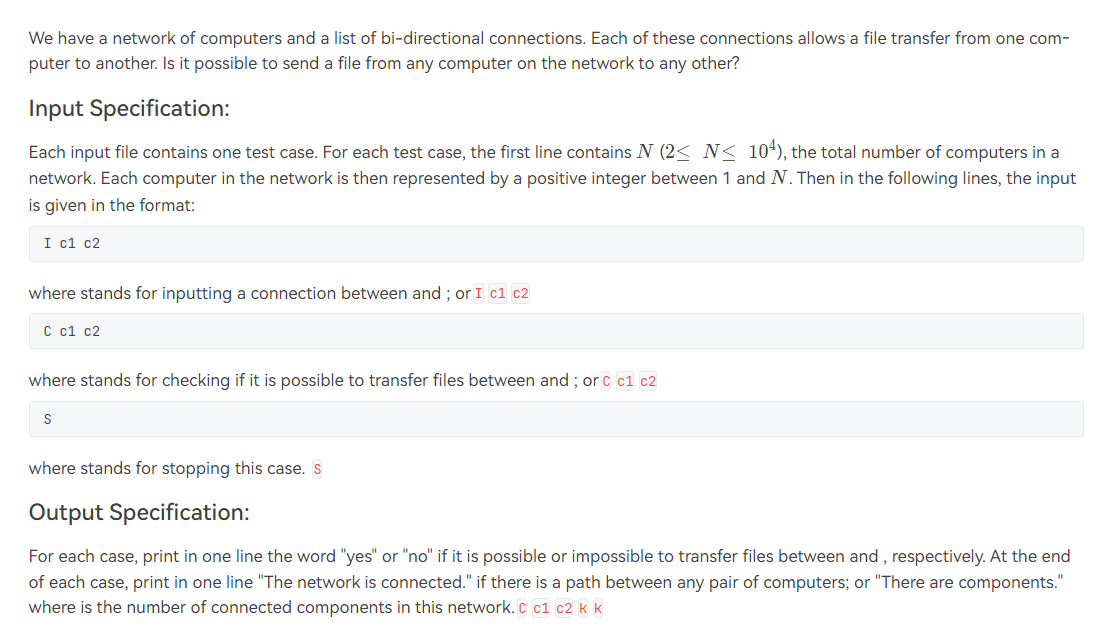
- Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
- Sample Output 1:
no
no
yes
There are 2 components.
- Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
- Sample Output 2:
no
no
yes
yes
The network is connected.
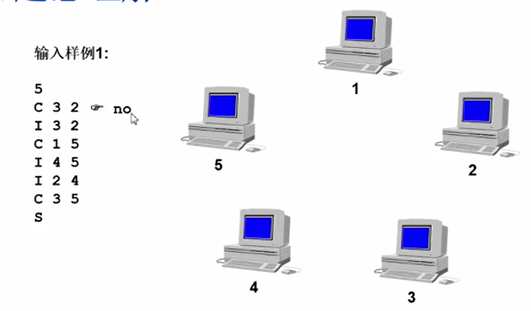
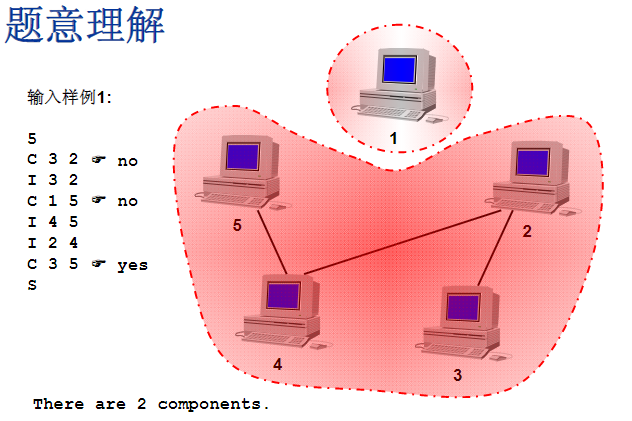
5代表计算机个数
C代表check表示查询3和2之间有没有联通,开始一条网线都没有,是不连通的,输出no
I 表示input输入,在3和2之间加一条网线…
S代表终止符
1自己是联通集(和自己联通),2,3,4,5是直接或间接联通的,所以输出系统里面有两个联通机
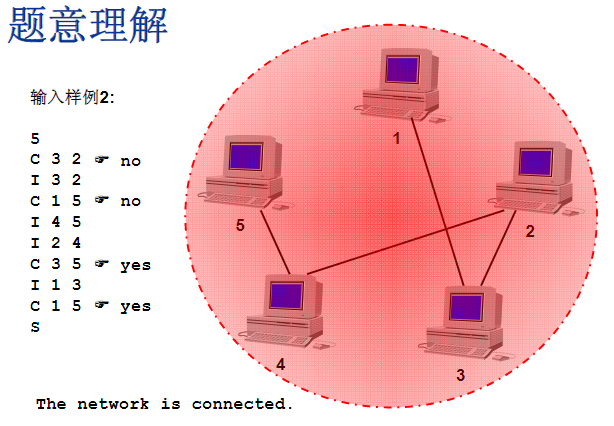
最后输出这个网络是联通的
程序框架搭建
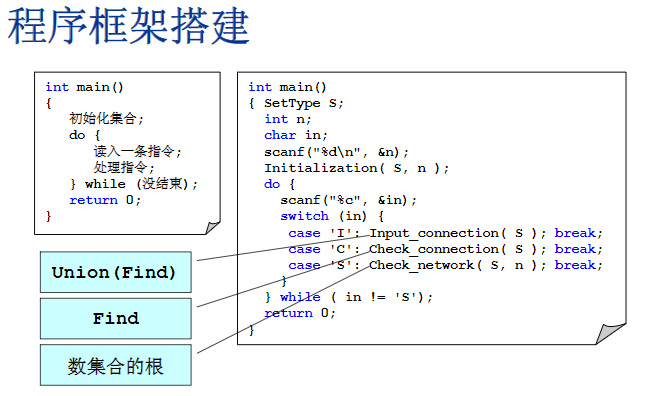
假设集合里的每个元素都是独立的,每一个都是自己的根节点,所以只要把S里面的每个元素都定义成-1就可以了

- Input_connection 输入函数:读进两个计算机的编号,计算机是从1到n编号的,而集合S的下标是从0到n-1的,要做一个简单的映射,调用Find函数的时候,传进去的是u这台计算机的下标u-1,v也类似,即读进来两台计算机,分别查一下它们两个所属集合的根结点是什么,如果他们俩个还分属于不同集合的话,就在之间连一条网线,也就是把这两个集合合并在一起
- Check_connection 查询函数:如果在check里面两个函数是一样的,就说明两个集合本身是联通的,输出yes,否则没联通就输出no
- Check_network 检查网络是否联通,参数n表示有多少个根结点,即返回多少个联通集。扫描每一个s数组里的元素,只要他是小于0的不一,那么他是一个根节点,
counter++;,最后数一下一共有多少个根节点,数完之后有两种情况,一种是只有一个根节点,表示整个集合全部联通了,否则就输出有多少个联通集
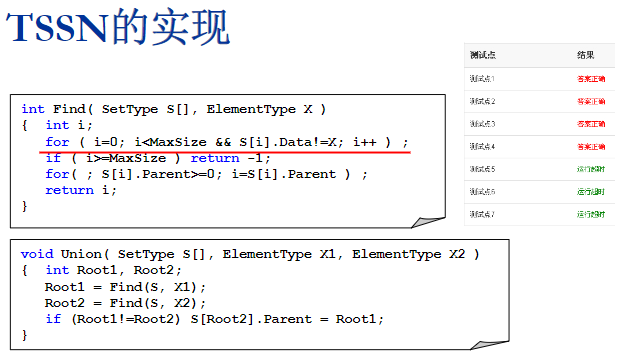
TSSN的实现
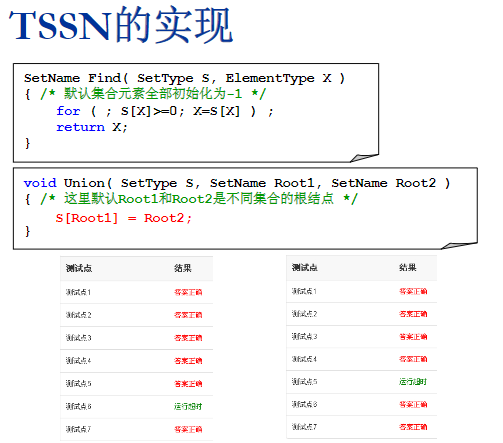
too simple sometimes naive(最原始简单版:很傻很天真)
按秩归并(对union的改进)

按高度归并
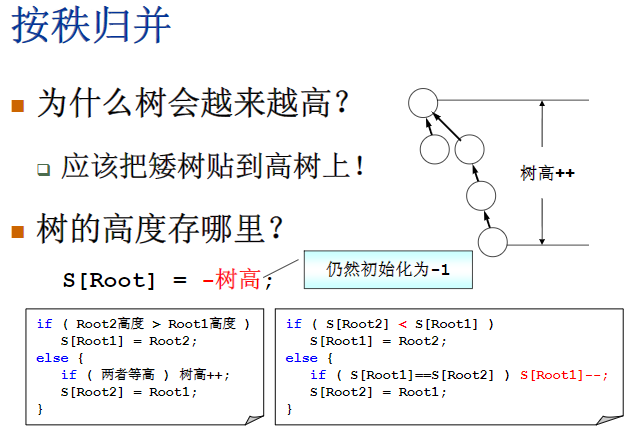
因为是负数,
,root2的高度要大于root1的高度,树高+1的话,意味着负值-1
按规模归并

任何时候归并了两棵树以后,最后结果树的规模都会改变,变成原来两棵树的规模之和,所以当集合2比较大的时候,把集合2的根节点做一个改变,加上原来集合1的规模,反之集合1规模改变,加上集合2的规模,
按秩归并最坏情况的树高:O(logN)
路径压缩(对find的改进)
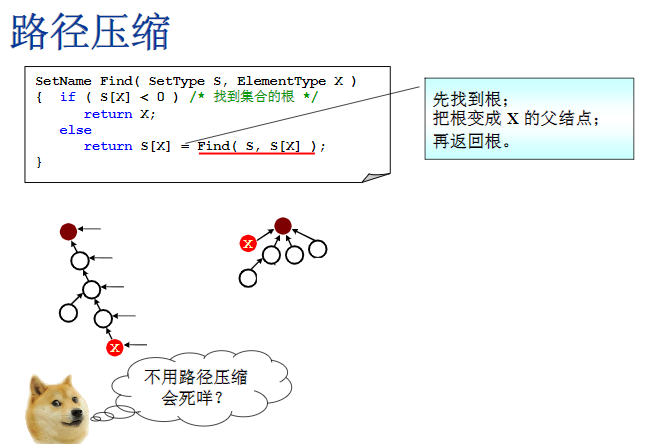
把路径上的每一个根节点都贴到了根节点的下面,该Find函数的递归调用实际上是一个伪递归,非常容易被转换成循环,不用担心系统堆栈爆掉。
- 尾递归基于函数的尾调用, 每一级调用直接返回函数的返回值更新调用栈,而不用创建新的调用栈, 类似迭代的实现, 时间和空间上均优化了一般递归!
时间复杂度

当N充分大的时候,路径压缩比不做效率快的多,但是N只有10的4次方的时候,logN是一个很小的数字,很难比较两种方法优劣。
源码
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 10001
typedef int ElementType;
typedef int SetName;
typedef ElementType SetType[MaxSize];
void Init(SetType s, int n) {
/*默认集合元素全部初始化为-1*/
/*for (; s[n]>=0; n=s[n])
return n;
*/
for (int i = 0; i < n; i++)
s[i] = -1;
}
/*路径压缩*/
SetName Find(SetType s, int x) {
if (s[x] < 0) // 本身已经是根
return x;
else // 先找到根,把根变成 x 的父结点,再返回根
return s[x] = Find(s, s[x]);
}
/*按秩(规模)归并*/
void Union(SetType s, SetName Root1, SetName Root2) {
//S[root] = -元素个数
if (s[Root1] < s[Root2]) { //x1的元素多,少的并入多的中
s[Root1] += s[Root2];
s[Root2] = Root1;
}
else {
s[Root2] += s[Root1];
s[Root1] = Root2;
}
}
/*输入函数*/
void Input_connection(SetType s) {
ElementType u, v;
scanf("%d %d", &u, &v);
SetName root1 = Find(s, u - 1); // 以数组下标存值,下标与存值差 1
SetName root2 = Find(s, v - 1);
if (root1 != root2)
Union(s, root1, root2);
}
/*查询函数*/
void check_connection(SetType s) {
ElementType u, v;
scanf("%d %d", &u, &v);
SetName root1 = Find(s, u - 1);
SetName root2 = Find(s, v - 1);
if (root1 == root2)
printf("yes\n");
else
printf("no\n");
}
/*检查网络是否联通,参数n表示有多少个根结点,即返回多少个联通集*/
void check_network(SetType s, int n) {
int counter = 0;
for (int i = 0; i < n; i++) {
if (s[i] < 0) counter++;
}
if (counter == 1)
printf("The network is connected.");
else
printf("There are %d components.", counter);
}
int main() {
SetType s;
int n;
char in;
scanf("%d\n", &n);
Init(s, n);
do {
//getchar();
scanf("%c", &in);
switch (in) {
case 'I':Input_connection(s); break;
case 'C':check_connection(s); break;
case 'S':check_network(s, n); break;
}
} while (in != 'S');
return 0;
}
运行
5
C 3 2
no
I 3 2
C 1 5
no
I 4 5
I 2 4
C 3 5
yes
S
There are 2 components.