题意理解

输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
老鼠的咒语最短
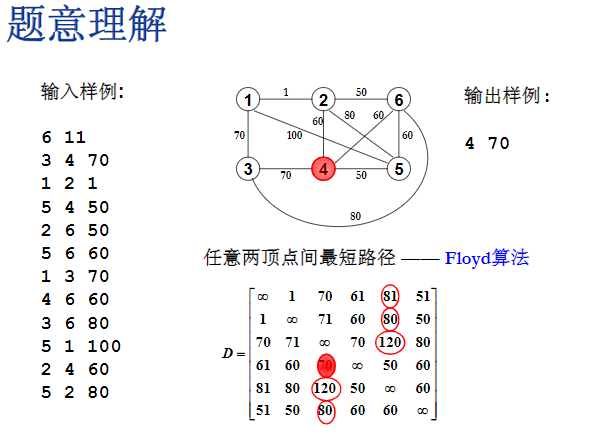
- 第一行,6表示动物的个数,也就是图里的顶点数,11表示的是边的个数
- 接下来每一行对应着一条边,对应的就是上面那张无向的网图
- 第一件事是把两个动物之间的最短路径找出来,在一个图里面找任意一对顶点之间最短路径,用
Floyd算法(多源最短路算法),之后得到一个最短距离的矩阵D,D(i,j)就是记录的从顶点 i 到顶点 j 之间的最短距离,比方说这个120是第三行第五列,从顶点3到顶点5之间的最短距离是120,就是D(3,5),其中动物编号是从1开始的- 回答Harry究竟带哪知动物去的这个问题的时候,首先检查每一行里面最大的那个数字,例如第一行里面最大的数字是81,就意味着第一个动物变成第5个动物是最麻烦的,从1变到5的距离最长,他的最短路径也有81,如果带第一个动物去,变成第五个动物是最麻烦的;以此类推,选第二个动物,变成第五个动物是最麻烦的;第三个动物,也是第五行;带第四号动物去,3难变;带第5号动物去,是3难变;带第6号动物去,是3难变;
- 带哪个动物去可使最难变的动物最好变?也就是圈出来的6个最大值里面,找那个最小值,也就是第四行的70,也就是把4号动物带去的话,最困难的一个动物是要变成3,最困难的咒语长度是70,已经是所有最困难的咒语里最容易的一个了,结论就是要带4号动物去,最难变咒语得长度是70
- 已知一个无向的网图,用
Floyd算法,去算任意两点之间的最短路径,然后对每一个顶点去扫描它到其他顶点的最短路径里面的最大值,把最大值记下来以后,就去找所有顶点里面最大值里面最小的那个值
程序框架搭建
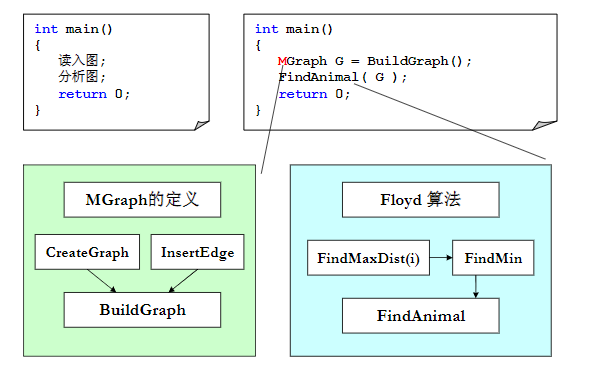
- 用
Floyd算法,把图表示成矩阵形式最合适,即用邻接矩阵表示的图- MGraph读入并建立图的话,调用
BuildGraph之前,必须CreateGraph建一个空图,然后不断地往这个空地图里面去插入边,就是一边读输入,一边把这个边插到这个图里去,有模板不用自己写,改改用就行- 第二个模块,就是首先调用一下Floyd算法,把这个图里面任意两点之间地最短路那个距离矩阵先得到,得到那个矩阵之后,我们就是要做这个
FindAnimal找要哪个动物去,这个函数涉及到求最大距离和最小距离的问题,也就是说先要对第 i 个动物去求他所有最短距离里面的最大值,然后再求所有这些最大值里面的最小值,然后把这个最小值交给这个FindAnimal这个函数最后去输出,就是整个程序的框架
选择动物

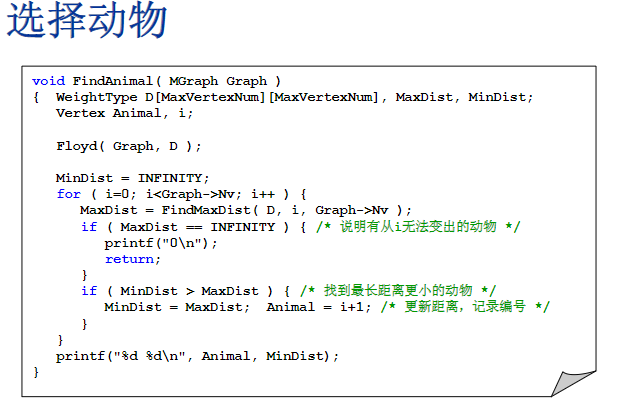
注意特殊情况:就是带一只动物去根本不可能,就是当图不连通的时候,图有不止一个连通集,所以带一只动物去是不可能的,当返回的这个
MaxDist无穷大的话就说明这个动物到其他动物最大距离是无穷大,就意味着从 i 开始,至少存在一个动物是他没有办法变出来的,所以直接输出一个0就回去了

先把
MaxDist初始化成一个很小的数,比如0,然后就对动物 i 来说,就扫描他的第 i 行,当 j 在变化的时候,如果某一个D[i][j]比当前的最大距离还要大的话,那就更新一下他的最大距离,邻接矩阵对角元最开始的时候是所有的两个顶点之间的距离都初始化为正无穷的,对角元是正无穷的总大于MaxDist,会造成永远返回正无穷,出错,加上i!=j就是把对角元跳过去了
模块的引用与裁剪
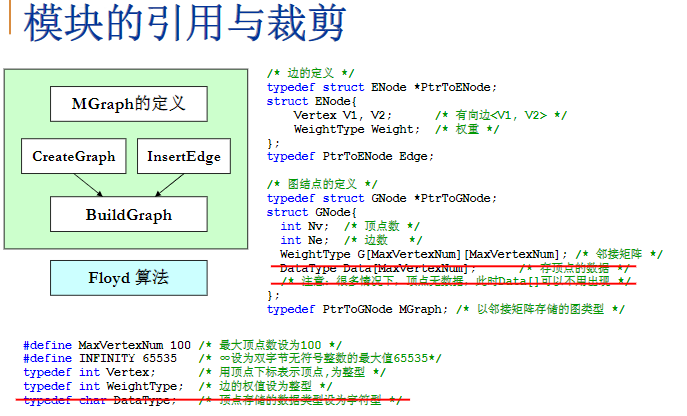
从下往上
- 顶点代表动物,不记录动物名字,可删一行
- 图节点里多余的就是顶点数据,因为不存在,删两行
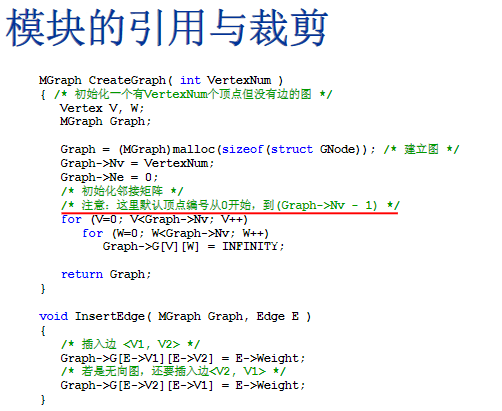

顶点读入数据
图的顶点从0开始编号,而本题目中动物从1开始编号。读输入时该如何处理使得图的相关模块可以顺利应用?
答E->V1--; E->V2--;
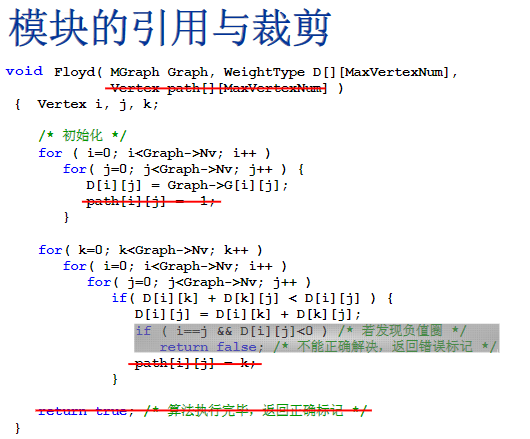
- 标准的
Floyd算法不仅要计算出任意两个顶点之间的最短距离这个数值,同时还要记录他们之间的这个路径,而在我们这道题里面是不需要记录路径的,和path相关的句子都可以删掉- 无负值圈,永远返回正,bool值就没必要了
代码
#include<stdio.h>
#include<stdlib.h>
#define MAX 100 /*最大顶点数设为100*/
#define INFINITY 65535 /*∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /*用顶点下标表示顶点,为整形*/
typedef int WeightType; /*边的权值设为整型*/
/*边的定义*/
typedef struct ENode *Edge;
struct ENode
{
Vertex V1;
Vertex V2; /*有向边<V1,V2>*/
WeightType Weight; /*权重*/
};
/*图结点的定义*/
typedef struct GNode *PtrtoGNode;
struct GNode //定义一个图的结构体
{
int Nv; /*顶点数*/
int Ne; /*边数*/
WeightType Graph[MAX][MAX]; /*邻接矩阵*/
};
typedef PtrtoGNode MGraph; /*以邻接矩阵存储的图类型*/
MGraph Create(int Vertexnum)
{ /*初始化一个有VertexNum个顶点但没有边的图*/
int i, j;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /*建立图*/
Graph->Nv = Vertexnum;
Graph->Ne = 0;
/*初始化邻接矩阵*/
/*注:这里默认顶点编号从0开始,到(Graph->Nv-1)*/
for (i = 0; i < Vertexnum; i++)
{
for (j = 0; j < Vertexnum; j++)
Graph-> Graph[i][j] = INFINITY;
}
return Graph;
}
//插入连接线
void InsertEdge(MGraph G, Edge E)
{ /*插入边<V1,V2>*/
G->Graph[E->V1][E->V2] = E->Weight; //在相应的邻接图存入相应的权重
/*若是无向图,还要插入边<V2,V1>*/
G->Graph[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
int Nv,i;
scanf("%d", &Nv); /*读入顶点个数*/
Graph = Create(Nv); /*初始化有Nv个顶点但没有边的图*/
scanf("%d", &(Graph->Ne)); /*读入边数*/
if (Graph->Ne != 0) /*如果有边*/
{
E = (Edge)malloc(sizeof(struct ENode));/*建立边结点*/
/*读入边,格式为"起点 终点 权重",插入邻接矩阵*/
for (i = 0; i < Graph->Ne; i++)
{
scanf("%d%d%d", &(E->V1), &(E->V2), &(E->Weight));
E->V2--; E->V1--; //因为输入边是从1开始的,而插入是从0开始的;(起始编号从0开始)
InsertEdge(Graph, E); //插入边
}
}
return Graph;
}
void Floyd(MGraph Graph, WeightType D[][MAX])
{
Vertex i, j, k;
for (i = 0; i < Graph->Nv; i++) //初始化,建立个和邻接图一样的二维数组
{
for (j = 0; j < Graph->Nv; j++)
{
D[i][j] = Graph->Graph[i][j];
}
}
/*进行判断*/
for (k = 0; k < Graph->Nv; k++)
for (i = 0; i < Graph->Nv; i++)
for (j = 0; j < Graph->Nv; j++)
if (D[i][j] > D[i][k] + D[k][j])
D[i][j] = D[i][k] + D[k][j];
}
int FindMax(WeightType D[][MAX], Vertex i, int n)
{
WeightType max = 0;
Vertex j;
for (j = 0; j < n; j++) { /*找出 i 到其他动物 j 的最长距离*/
if (i != j && D[i][j] > max)
max = D[i][j];
}
return max;
}
void find(MGraph Graph)
{
WeightType D[MAX][MAX], Max = 0, Min = INFINITY;
Vertex Animal, i;
Floyd(Graph, D);
for (i = 0; i < Graph->Nv; i++)
{
Max = FindMax(D, i, Graph->Nv);
if (Max == INFINITY) /*说明有从i无法变出的动物*/
{
printf("0\n");
return;
}
if (Max < Min) /*找到最长距离更小的动物*/
{
Min = Max;
Animal = i + 1; /*更新距离,记录编号*/
}
}
printf("%d %d\n", Animal, Min);
}
int main() {
MGraph G = BuildGraph();
find(G);
}
运行
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
4 70