最小表示法

说来也不难，最小表示法，就是给你一个环型的字符串，然后你把它从任意位置，破圆成链，然后在形成的不同的串中，找到字典序最小的那一个。

我们的做法就是，把字符串延长一倍，然后用两个指针，一个从0开始，一个从1开始，往后比较每一个长度为n的字符串，这里设为指针i， j。

比较的时候直接暴力比较，如图
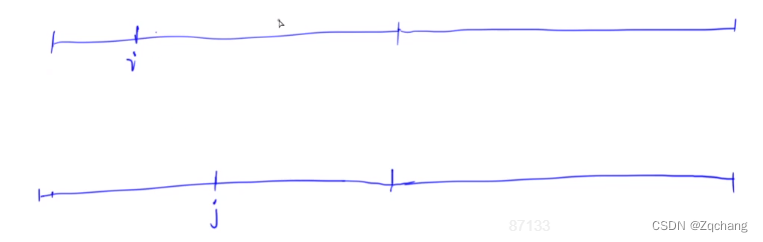
在这里插入图片描述
先比较第一个，如果相同就比较下一个，如果不同的话，就让大的那个指针，往后移，假设是第k个不一样，i = i + k + 1；因为这期间从i到k里面，每一个都会有一个对应的字符串，而且在k那个位置比它小，所以要从k+1开始再次比较

如果找到了俩串一样，并且i != j，这时候就说明原串是一个循环串，并且i和j之间就是第一个循环节，而且已经枚举过了。如果是一个循环串，那么不同的起点只有一个循环节这么多，从下个循环节就又重复了，这个时候就能直接break了

项链

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2000010;

int n;
char a[N], b[N];

int get_min(char s[])
{
    int i = 0, j = 1;
    while (i < n && j < n)
    {
        int k = 0;
        while (k < n && s[i + k] == s[j + k]) k ++ ;//比较
        if (k == n) break;//如果俩串一样，就break
        if (s[i + k] > s[j + k]) i += k + 1;
        else j += k + 1;//就是刚刚推到的
        if (i == j) j ++ ;//如果相同的话，没必要比较比较了可能还会误导
    }
    int k = min(i, j);
    s[k + n] = 0;
    return k;
}

int main()
{
    scanf("%s%s", a, b);
    n = strlen(a);
    memcpy(a + n, a, n);
    memcpy(b + n, b, n);

    int x = get_min(a), y = get_min(b);
    if (strcmp(a + x, b + y)) puts("No");
    else
    {
        puts("Yes");
        puts(a + x);
    }

    return 0;
}

构造

直接给两个例题吧，一般这种题都是在一个数学结论基础上搞出来的

神奇的幻方

简单的原因是因为给出来构造方法了

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 40;

int n;
int a[N][N];

int main()
{
    cin >> n;

    int x = 1, y = n / 2 + 1;
    for (int i = 1; i <= n * n; i ++ )
    {
        a[x][y] = i;
        if (x == 1 && y == n) x ++ ;
        else if (x == 1) x = n, y ++ ;
        else if (y == n) x --, y = 1;
        else if (a[x - 1][y + 1]) x ++ ;
        else x --, y ++ ;
    }

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= n; j ++ ) printf("%d ", a[i][j]);
        puts("");
    }

    return 0;
}

时态同步

意思就是要让子节点到根节点的时间都一样，如果你上来就想算出来从根节点到每个子节点的时间，然后用最大的求差累加的话，是错的，因为有可能，不同的子节点共用了一段路，这时候，只需要给这段路加上一些时间就可以了，不用累加多次

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;
const int N = 500010, M = N * 2;

int n, root;
int h[N], e[M], w[M], ne[M], idx;
LL d[N], ans;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u, int father)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
        d[u] = max(d[u], d[j] + (LL)w[i]);
    }
    
    
    // d[u] += d[e[h[u]]];
    
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        ans += d[u] - (d[j] + w[i]);
    }
}

int main()
{
    scanf("%d%d", &n, &root);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    dfs(root, -1);
    printf("%lld\n", ans);

    return 0;
}