通常在处理传感器数据(或信号)时,我们会发现数据通常不干净并且存在大量噪声。这种噪声使得执行进一步的数学运算变得更加困难,例如微分、积分、卷积等。此外,如果我们打算将这些信号用于控制自动驾驶汽车、机器人等实时操作,那么这种噪声会带来很大的挑战。手臂或工业厂房,因为噪声往往会在任何下游数学运算中放大。
在这种情况下,一种通用方法是平滑数据以去除噪声。我们寻求实时平滑这些数据,以用于控制工程中的应用,例如自动驾驶汽车或机器人的智能控制。已经开发了许多方法来实时平滑信号,例如卡尔曼滤波器、扩展卡尔曼滤波器及其变体。然而,设计卡尔曼滤波器需要了解系统动力学,这可能是已知的,也可能是未知的。在这种情况下,一种更简单的方法是对收到的最后一个数据点执行最小二乘多项式拟合。n
最小二乘多项式拟合的数学非常简单。考虑一组n个数据点
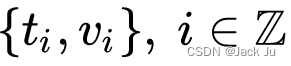
在这种情况下,阶多项式拟合k可以写成:
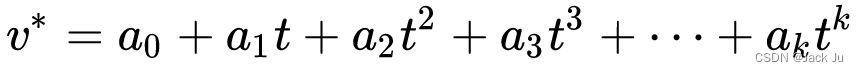
等式 1
在这种情况下,残差由下式给出
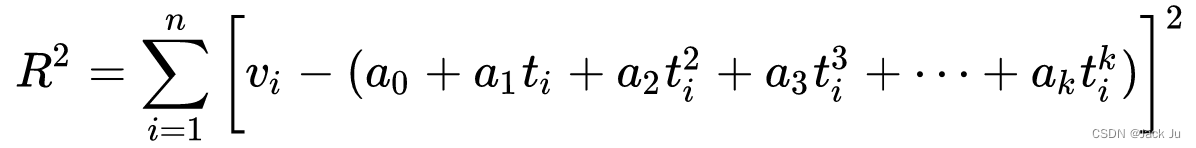
等式 2
最小二乘多项式拟合的目标是最小化R2。通常的方法是对等式 2 对系数a 进行偏导并使其为零。这导致了一个由k个方程组成的系统。这样的方程组以范德蒙矩阵方程的形式出现,可以简化并写成如下:
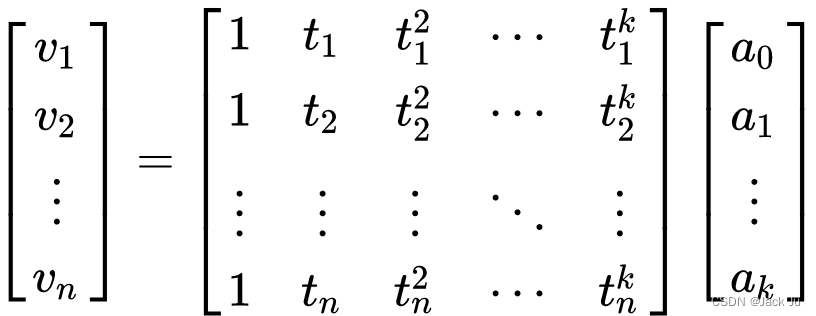
等式 3
在矩阵表示法中,我们可以将等式 3 写为
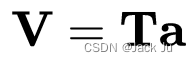
等式 4
等式 4 可以通过预乘T的转置来求解,因此解向量为

等式 5
最小二乘多项式拟合的实现
正如一开始所说,这里关注的应用是一个实时系统,它可能必须处理安全关键系统,例如自动驾驶汽车和机械臂。对于这样的系统,在目标通常是嵌入式系统的情况下,实现速度很重要。因此,在 C++ 中实现的编程语言的常见选择。在本文中,我们使用用 C++ 编写的 Eigen 包来求解方程 5。
对于从乘用车的速度曲线获得的样本数据点,下面提供了实现代码。我只是拟合了一个三次多项式。请注意,拟合更高次的多项式计算成本很高,可能根本不需要。
具体代码如下
#include <Eigen/Dense>
#include <iostream>
#include <cmath>
#include <vector>
#include <Eigen/QR>
#include "matplotlibcpp.h"
namespace plt = matplotlibcpp;
void polyfit( const std::vector<double> &t,
const std::vector<double> &v,
std::vector<double> &coeff,
int order
)
{
// Create Matrix Placeholder of size n x k, n= number of datapoints, k = order of polynomial, for exame k = 3 for cubic polynomial
Eigen::MatrixXd T(t.size(), order + 1);
Eigen::VectorXd V = Eigen::VectorXd::Map(&v.front(), v.size());
//std::cout<<"ceshi"<<std::endl;
//std::cout<<V<<std::endl;
Eigen::VectorXd result;
// check to make sure inputs are correct
assert(t.size() == v.size());
assert(t.size() >= order + 1);
// Populate the matrix
for(size_t i = 0 ; i < t.size(); ++i)
{
for(size_t j = 0; j < order + 1; ++j)
{
T(i, j) = pow(t.at(i), j);
}
}
std::cout<<T<<std::endl;
// Solve for linear least square fit
result = T.householderQr().solve(V);
coeff.resize(order+1);
for (int k = 0; k < order+1; k++)
{
coeff[k] = result[k];
}
}
int main()
{
// time value
std::vector<double> time = {0, 0.0192341804504395, 0.0394501686096191, 0.059575080871582, 0.0790810585021973, 0.0792751312255859, 0.0987141132354736, 0.119336366653442, 0.138712167739868, 0.159000158309937, 0.178890228271484, 0.19960618019104, 0.219112157821655, 0.23919415473938, 0.259442090988159, 0.279186248779297, 0.299112319946289, 0.319219350814819, 0.339494228363037, 0.339675188064575, 0.359552145004272, 0.37941837310791, 0.399189233779907, 0.419828176498413, 0.439810276031494, 0.459331274032593, 0.479461193084717, 0.499663114547729, 0.519809246063232, 0.539092063903809, 0.559118270874023, 0.579315185546875, 0.598889112472534, 0.619685173034668, 0.638863086700439, 0.639052152633667, 0.658920288085938, 0.679149150848389, 0.699787139892578, 0.71905517578125, 0.73898720741272, 0.739143371582031, 0.758654117584229, 0.779210329055786, 0.799195289611816, 0.819046258926392, 0.839539289474487, 0.85923433303833, 0.87903618812561, 0.899263143539429, 0.919251203536987, 0.939138174057007, 0.959244251251221, 0.979074239730835, 0.998935222625732, 1.01904726028442, 1.0387852191925, 1.03895926475525, 1.05906510353088, 1.07873225212097, 1.09908628463745, 1.11907029151917, 1.13899827003479, 1.15879201889038};
// velocity value
std::vector<double> velocity = {1.8, 1.86, 2.03, 2.08, 2.14, 2.14, 2.25, 2.36, 2.42, 2.59, 2.7, 2.81, 2.87, 3.04, 3.15, 3.26, 3.32, 3.43, 3.54, 3.54, 3.6, 3.71, 3.83, 3.94, 4.11, 4.22, 4.33, 4.44, 4.56, 4.67, 4.78, 4.84, 4.84, 4.89, 4.89, 4.89, 4.95, 5.01, 5.06, 5.06, 5.06, 5.06, 5.01, 5.06, 5.12, 5.18, 5.18, 5.23, 5.23, 5.23, 5.29, 5.34, 5.29, 5.4, 5.4, 5.46, 5.51, 5.51, 5.51, 5.46, 5.4, 5.34, 5.34, 5.34};
// placeholder for storing polynomial coefficient
std::vector<double> coeff;
polyfit(time, velocity, coeff, 3);
std::vector<double> fitted_velocity;
std::cout<< "Printing fitted values" << std::endl;
for(int p = 0; p < time.size(); ++ p)
{
double vfitted = coeff[0] + coeff[1]*time.at(p) + coeff[2]*(pow(time.at(p), 2)) +coeff[3]*(pow(time.at(p), 3)) ;
std::cout<< vfitted<<", ";
fitted_velocity.push_back(vfitted);
}
std::cout<<std::endl;
/*原始数据*/
plt::figure();
//plt::subplot(2,2,1);
plt::title("originaldata");
plt::plot(time,velocity);
plt::figure();
/*最小二乘拟合后的数据*/
//plt::subplot(2,2,2);
plt::title("polyfitdata");
plt::plot(time,fitted_velocity);
plt::show();
return 0;
}
CmakeList配置:
CMAKE_MINIMUM_REQUIRED(VERSION 2.8)
PROJECT(polyfit)
set(CMAKE_CXX_STANDARD 11)
INCLUDE_DIRECTORIES("/usr/include/eigen3") #("${EIGEN3_INCLUDE_DIR}")
#SET(EIGEN3_INCLUDE_DIR "$ENV{EIGEN3_INCLUDE_DIR}")
#IF(NOT EIGEN3_INCLUDE_DIR)
# MESSAGE( FATAL_ERROR "Please point the environment variable EIGEN3_INCLUDE_DIR to the include directory of your Eigen3 installation.")
#ENDIF()
#INCLUDE_DIRECTORIES(/usr/include/eigen3) #("${EIGEN3_INCLUDE_DIR}")
#ADD_EXECUTABLE(test test.cpp)
#include_directories(src)
# 找到src目录及其子目录下的所有c文件和h文件
#file(GLOB_RECURSE PROJECT_SOURCES "src/*.cpp" "src/*.c" "src/*.cc")
set(sources src/eigen_polyfit.cpp)
add_executable(polyfit ${sources})
#file(GLOB_RECURSE PROJECT_HEADERS "src/*.hpp" "src/*.h" "src/*.hh")
#add_executable(polyfit ${PROJECT_SOURCES} ${PROJECT_HEADERS})
target_link_libraries(polyfit python2.7)
使用matplotlib-cpp可视化效果如下图:
拟合后的效果:

原始数据:

完整工程代码见https://github.com/JackJu-HIT/Polyfit.git。
